Question-96032

Question Number 96032 by i jagooll last updated on 29/May/20

Commented by i jagooll last updated on 29/May/20

ABCD is a square with an area 240 cm^2 if DP = 3PC , then what is the area of the shaded region ?

$$\mathrm{ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square}\:\mathrm{with}\:\mathrm{an}\:\mathrm{area}\:\mathrm{240}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{if}\:\mathrm{DP}\:=\:\mathrm{3PC}\:,\:\mathrm{then}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{region}\:? \\ $$

Commented by mr W last updated on 29/May/20

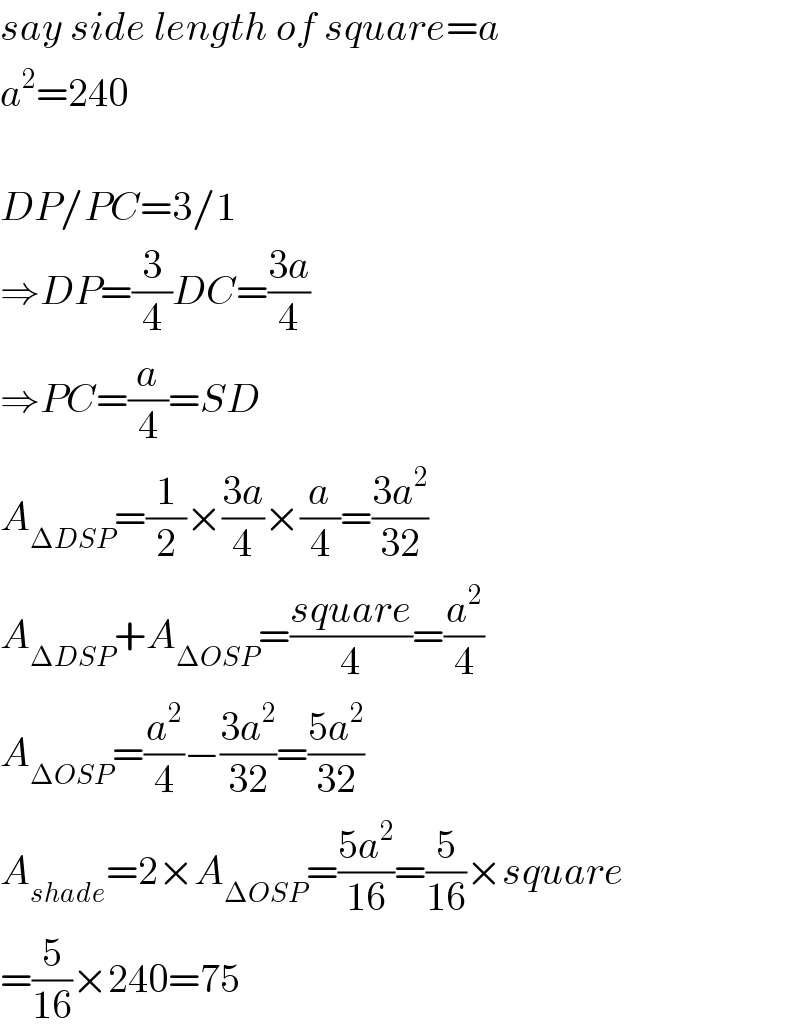
say side length of square=a a^2 =240 DP/PC=3/1 ⇒DP=(3/4)DC=((3a)/4) ⇒PC=(a/4)=SD A_(ΔDSP) =(1/2)×((3a)/4)×(a/4)=((3a^2 )/(32)) A_(ΔDSP) +A_(ΔOSP) =((square)/4)=(a^2 /4) A_(ΔOSP) =(a^2 /4)−((3a^2 )/(32))=((5a^2 )/(32)) A_(shade) =2×A_(ΔOSP) =((5a^2 )/(16))=(5/(16))×square =(5/(16))×240=75

$${say}\:{side}\:{length}\:{of}\:{square}={a} \\ $$$${a}^{\mathrm{2}} =\mathrm{240} \\ $$$$ \\ $$$${DP}/{PC}=\mathrm{3}/\mathrm{1} \\ $$$$\Rightarrow{DP}=\frac{\mathrm{3}}{\mathrm{4}}{DC}=\frac{\mathrm{3}{a}}{\mathrm{4}} \\ $$$$\Rightarrow{PC}=\frac{{a}}{\mathrm{4}}={SD} \\ $$$${A}_{\Delta{DSP}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}{a}}{\mathrm{4}}×\frac{{a}}{\mathrm{4}}=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{32}} \\ $$$${A}_{\Delta{DSP}} +{A}_{\Delta{OSP}} =\frac{{square}}{\mathrm{4}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}_{\Delta{OSP}} =\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{32}}=\frac{\mathrm{5}{a}^{\mathrm{2}} }{\mathrm{32}} \\ $$$${A}_{{shade}} =\mathrm{2}×{A}_{\Delta{OSP}} =\frac{\mathrm{5}{a}^{\mathrm{2}} }{\mathrm{16}}=\frac{\mathrm{5}}{\mathrm{16}}×{square} \\ $$$$=\frac{\mathrm{5}}{\mathrm{16}}×\mathrm{240}=\mathrm{75} \\ $$

Commented by i jagooll last updated on 29/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\: \\ $$

Answered by john santu last updated on 29/May/20

Commented by john santu last updated on 29/May/20

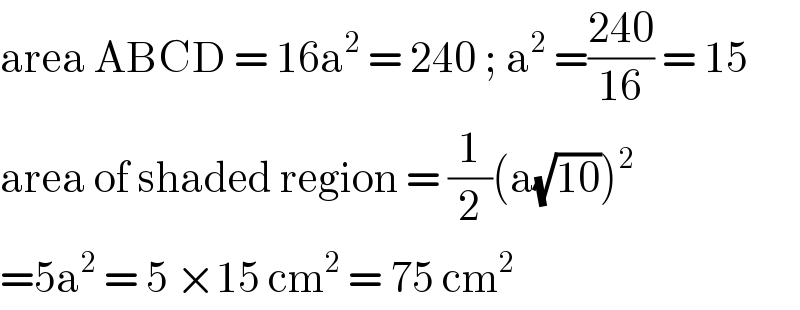
area ABCD = 16a^2 = 240 ; a^2 =((240)/(16)) = 15 area of shaded region = (1/2)(a(√(10)))^2 =5a^2 = 5 ×15 cm^2 = 75 cm^2

$$\mathrm{area}\:\mathrm{ABCD}\:=\:\mathrm{16a}^{\mathrm{2}} \:=\:\mathrm{240}\:;\:\mathrm{a}^{\mathrm{2}} \:=\frac{\mathrm{240}}{\mathrm{16}}\:=\:\mathrm{15} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{region}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{a}\sqrt{\mathrm{10}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{5a}^{\mathrm{2}} \:=\:\mathrm{5}\:×\mathrm{15}\:\mathrm{cm}^{\mathrm{2}} \:=\:\mathrm{75}\:\mathrm{cm}^{\mathrm{2}} \: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply