Question Number 96089 by bebo last updated on 29/May/20

Answered by mr W last updated on 30/May/20

Commented by mr W last updated on 30/May/20
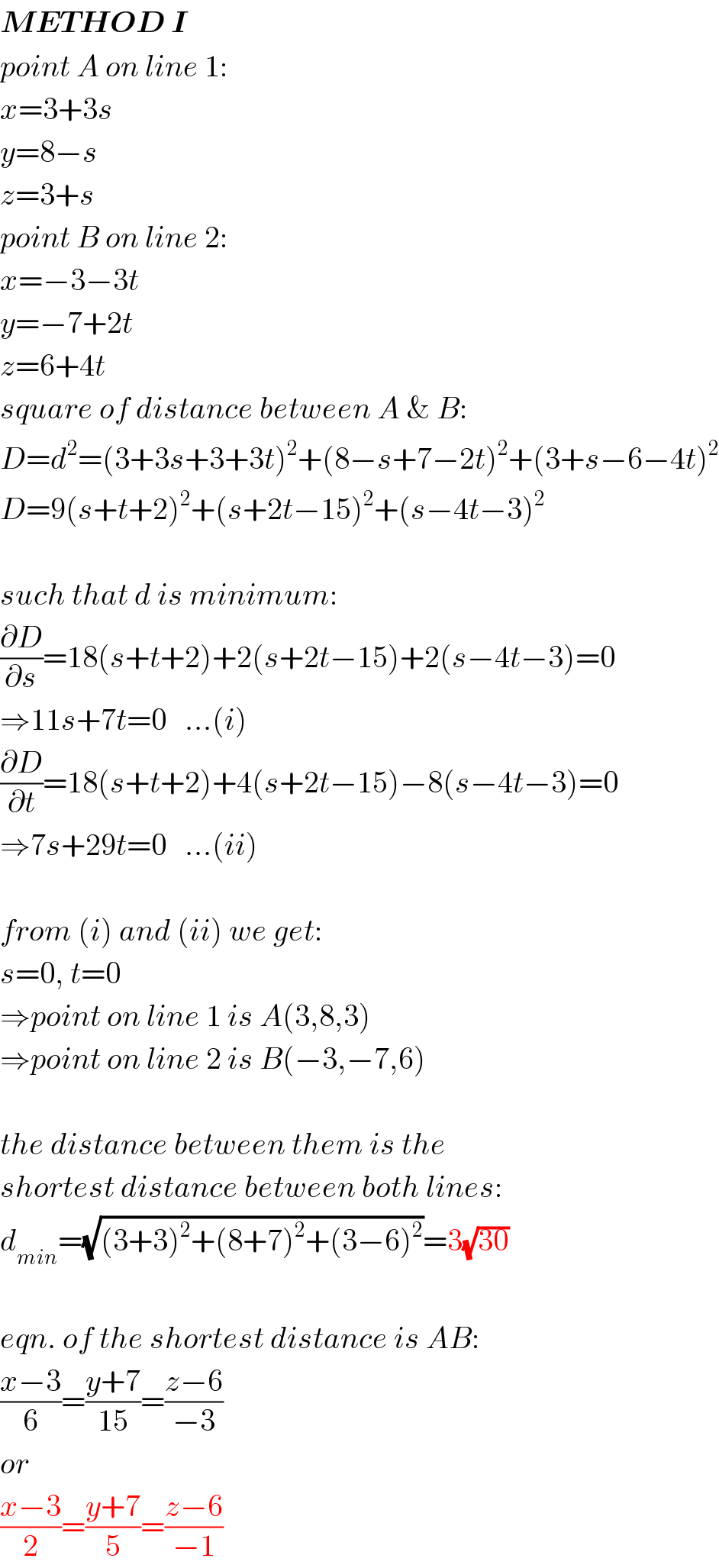
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${point}\:{A}\:{on}\:{line}\:\mathrm{1}: \\ $$$${x}=\mathrm{3}+\mathrm{3}{s} \\ $$$${y}=\mathrm{8}−{s} \\ $$$${z}=\mathrm{3}+{s} \\ $$$${point}\:{B}\:{on}\:{line}\:\mathrm{2}: \\ $$$${x}=−\mathrm{3}−\mathrm{3}{t} \\ $$$${y}=−\mathrm{7}+\mathrm{2}{t} \\ $$$${z}=\mathrm{6}+\mathrm{4}{t} \\ $$$${square}\:{of}\:{distance}\:{between}\:{A}\:\&\:{B}: \\ $$$${D}={d}^{\mathrm{2}} =\left(\mathrm{3}+\mathrm{3}{s}+\mathrm{3}+\mathrm{3}{t}\right)^{\mathrm{2}} +\left(\mathrm{8}−{s}+\mathrm{7}−\mathrm{2}{t}\right)^{\mathrm{2}} +\left(\mathrm{3}+{s}−\mathrm{6}−\mathrm{4}{t}\right)^{\mathrm{2}} \\ $$$${D}=\mathrm{9}\left({s}+{t}+\mathrm{2}\right)^{\mathrm{2}} +\left({s}+\mathrm{2}{t}−\mathrm{15}\right)^{\mathrm{2}} +\left({s}−\mathrm{4}{t}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${such}\:{that}\:{d}\:{is}\:{minimum}: \\ $$$$\frac{\partial{D}}{\partial{s}}=\mathrm{18}\left({s}+{t}+\mathrm{2}\right)+\mathrm{2}\left({s}+\mathrm{2}{t}−\mathrm{15}\right)+\mathrm{2}\left({s}−\mathrm{4}{t}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{11}{s}+\mathrm{7}{t}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{D}}{\partial{t}}=\mathrm{18}\left({s}+{t}+\mathrm{2}\right)+\mathrm{4}\left({s}+\mathrm{2}{t}−\mathrm{15}\right)−\mathrm{8}\left({s}−\mathrm{4}{t}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{7}{s}+\mathrm{29}{t}=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}: \\ $$$${s}=\mathrm{0},\:{t}=\mathrm{0} \\ $$$$\Rightarrow{point}\:{on}\:{line}\:\mathrm{1}\:{is}\:{A}\left(\mathrm{3},\mathrm{8},\mathrm{3}\right) \\ $$$$\Rightarrow{point}\:{on}\:{line}\:\mathrm{2}\:{is}\:{B}\left(−\mathrm{3},−\mathrm{7},\mathrm{6}\right) \\ $$$$ \\ $$$${the}\:{distance}\:{between}\:{them}\:{is}\:{the} \\ $$$${shortest}\:{distance}\:{between}\:{both}\:{lines}: \\ $$$${d}_{{min}} =\sqrt{\left(\mathrm{3}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{8}+\mathrm{7}\right)^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{6}\right)^{\mathrm{2}} }=\mathrm{3}\sqrt{\mathrm{30}} \\ $$$$ \\ $$$${eqn}.\:{of}\:{the}\:{shortest}\:{distance}\:{is}\:{AB}: \\ $$$$\frac{{x}−\mathrm{3}}{\mathrm{6}}=\frac{{y}+\mathrm{7}}{\mathrm{15}}=\frac{{z}−\mathrm{6}}{−\mathrm{3}} \\ $$$${or} \\ $$$$\frac{{x}−\mathrm{3}}{\mathrm{2}}=\frac{{y}+\mathrm{7}}{\mathrm{5}}=\frac{{z}−\mathrm{6}}{−\mathrm{1}} \\ $$
Commented by mr W last updated on 30/May/20
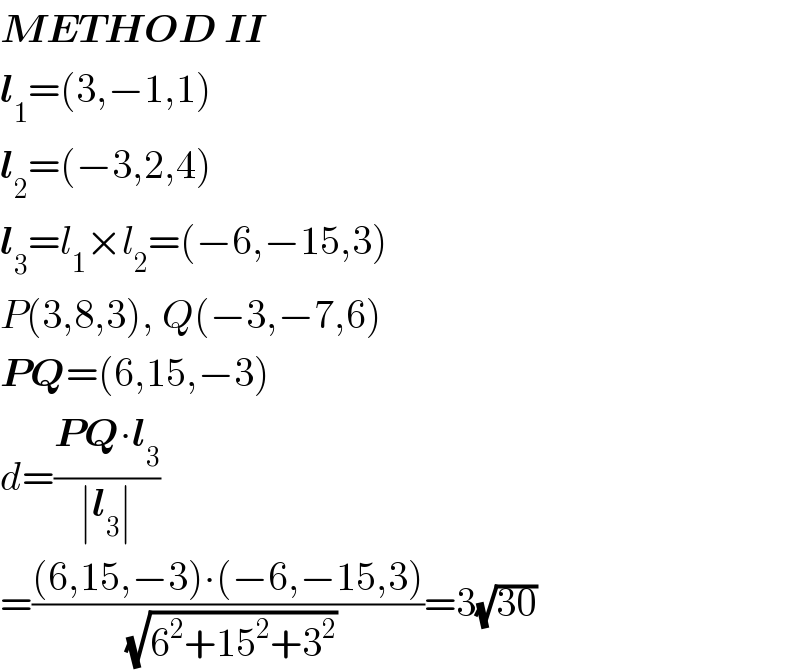
$$\boldsymbol{{METHOD}}\:\boldsymbol{{II}} \\ $$$$\boldsymbol{{l}}_{\mathrm{1}} =\left(\mathrm{3},−\mathrm{1},\mathrm{1}\right) \\ $$$$\boldsymbol{{l}}_{\mathrm{2}} =\left(−\mathrm{3},\mathrm{2},\mathrm{4}\right) \\ $$$$\boldsymbol{{l}}_{\mathrm{3}} ={l}_{\mathrm{1}} ×{l}_{\mathrm{2}} =\left(−\mathrm{6},−\mathrm{15},\mathrm{3}\right) \\ $$$${P}\left(\mathrm{3},\mathrm{8},\mathrm{3}\right),\:{Q}\left(−\mathrm{3},−\mathrm{7},\mathrm{6}\right) \\ $$$$\boldsymbol{{PQ}}=\left(\mathrm{6},\mathrm{15},−\mathrm{3}\right) \\ $$$${d}=\frac{\boldsymbol{{PQ}}\centerdot\boldsymbol{{l}}_{\mathrm{3}} }{\mid\boldsymbol{{l}}_{\mathrm{3}} \mid} \\ $$$$=\frac{\left(\mathrm{6},\mathrm{15},−\mathrm{3}\right)\centerdot\left(−\mathrm{6},−\mathrm{15},\mathrm{3}\right)}{\:\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }}=\mathrm{3}\sqrt{\mathrm{30}} \\ $$
Answered by Sourav mridha last updated on 30/May/20
![((x+3)/(−3))=((y+7)/2)=((z−6)/4) this line is going through the point (say)p(−3,−7,6) for the straight line−− ((x−3)/3)=((y−8)/(−1))=((z−3)/1),any point on this line described by a parameter t ,like that L(3+3t,8−t,3+t). the shortest distance means the perpendicular distance bet^n this two lines,lets say ⊥_r distance is PL.(([ the DR of PL is [6+3t,15−t,−3+t] PL is both ⊥_r to two lines so: 3(6+3t)−1(15−t)+1(−3+t)=0 ⇒18+9t−15+t−3+t=0 so t=0 the poit L(3,8,3) and we know p(−3,−7,6) so ∣PL∣=(√(6^2 +15^2 +3^2 ))=(√(270))=3(√(30))unit now the eq^n of PL in cartetian form ((x+3)/6)=((y+7)/(15))=((z−6)/(−3)) or in vector form r=(−3i^� −7j^� +6k^� )+t(6i^� +15j^� −3k^� )](https://www.tinkutara.com/question/Q96162.png)
$$\frac{\mathrm{x}+\mathrm{3}}{−\mathrm{3}}=\frac{\mathrm{y}+\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{z}−\mathrm{6}}{\mathrm{4}}\:\mathrm{this}\:\mathrm{line}\:\mathrm{is}\:\mathrm{going}\: \\ $$$$\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{say}\right)\boldsymbol{\mathrm{p}}\left(−\mathrm{3},−\mathrm{7},\mathrm{6}\right) \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{straight}\:\mathrm{line}−− \\ $$$$\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}=\frac{\mathrm{y}−\mathrm{8}}{−\mathrm{1}}=\frac{\mathrm{z}−\mathrm{3}}{\mathrm{1}},\mathrm{any}\:\mathrm{point}\:\mathrm{on}\:\mathrm{this}\:\mathrm{line} \\ $$$$\mathrm{described}\:\mathrm{by}\:\mathrm{a}\:\mathrm{parameter}\:\boldsymbol{\mathrm{t}}\:,\mathrm{like}\:\mathrm{that} \\ $$$$\mathrm{L}\left(\mathrm{3}+\mathrm{3t},\mathrm{8}−\boldsymbol{\mathrm{t}},\mathrm{3}+\mathrm{t}\right). \\ $$$$\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{means}\:\mathrm{the} \\ $$$$\mathrm{perpendicular}\:\mathrm{distance}\:\mathrm{bet}^{\mathrm{n}} \:\mathrm{this}\:\mathrm{two} \\ $$$$\mathrm{lines},\mathrm{lets}\:\mathrm{say}\:\bot_{\mathrm{r}} \:\mathrm{distance}\:\mathrm{is}\:\mathrm{P}\boldsymbol{\mathrm{L}}.\left(\left(\left[\right.\right.\right. \\ $$$$\mathrm{the}\:\mathrm{DR}\:\mathrm{of}\:\mathrm{PL}\:\mathrm{is} \\ $$$$\left[\mathrm{6}+\mathrm{3t},\mathrm{15}−\mathrm{t},−\mathrm{3}+\mathrm{t}\right] \\ $$$$\mathrm{PL}\:\mathrm{is}\:\mathrm{both}\:\bot_{\mathrm{r}} \:\mathrm{to}\:\mathrm{two}\:\mathrm{lines}\:\mathrm{so}: \\ $$$$\mathrm{3}\left(\mathrm{6}+\mathrm{3t}\right)−\mathrm{1}\left(\mathrm{15}−\mathrm{t}\right)+\mathrm{1}\left(−\mathrm{3}+\mathrm{t}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{18}+\mathrm{9t}−\mathrm{15}+\mathrm{t}−\mathrm{3}+\mathrm{t}=\mathrm{0} \\ $$$$\mathrm{so}\:\:\:\:\:\boldsymbol{{t}}=\mathrm{0} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{poit}}\:\boldsymbol{{L}}\left(\mathrm{3},\mathrm{8},\mathrm{3}\right) \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{know}\:\boldsymbol{{p}}\left(−\mathrm{3},−\mathrm{7},\mathrm{6}\right) \\ $$$$\mathrm{so}\:\mid\boldsymbol{{PL}}\mid=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\mathrm{270}}=\mathrm{3}\sqrt{\mathrm{30}}\mathrm{unit} \\ $$$$\mathrm{now}\:\mathrm{the}\:\mathrm{eq}^{\mathrm{n}} \:\mathrm{of}\:\boldsymbol{{PL}}\:\mathrm{in}\:\mathrm{cartetian}\:\mathrm{form} \\ $$$$\:\:\:\:\:\frac{\boldsymbol{{x}}+\mathrm{3}}{\mathrm{6}}=\frac{\boldsymbol{{y}}+\mathrm{7}}{\mathrm{15}}=\frac{\boldsymbol{{z}}−\mathrm{6}}{−\mathrm{3}} \\ $$$$\boldsymbol{{or}}\:\boldsymbol{{in}}\:\boldsymbol{{vector}}\:\boldsymbol{{form}} \\ $$$$\boldsymbol{{r}}=\left(−\mathrm{3}\hat {\mathrm{i}}−\mathrm{7}\hat {\mathrm{j}}+\mathrm{6}\hat {\mathrm{k}}\right)+\mathrm{t}\left(\mathrm{6}\hat {\mathrm{i}}+\mathrm{15}\hat {\mathrm{j}}−\mathrm{3}\hat {\mathrm{k}}\right) \\ $$
