Question-96155

Question Number 96155 by pticantor last updated on 30/May/20

Commented by prakash jain last updated on 30/May/20

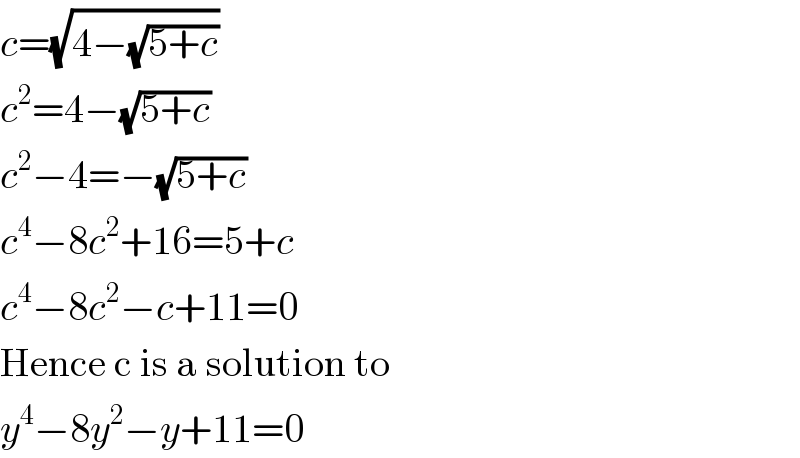
c=(√(4−(√(5+c)))) c^2 =4−(√(5+c)) c^2 −4=−(√(5+c)) c^4 −8c^2 +16=5+c c^4 −8c^2 −c+11=0 Hence c is a solution to y^4 −8y^2 −y+11=0

$${c}=\sqrt{\mathrm{4}−\sqrt{\mathrm{5}+{c}}} \\ $$$${c}^{\mathrm{2}} =\mathrm{4}−\sqrt{\mathrm{5}+{c}} \\ $$$${c}^{\mathrm{2}} −\mathrm{4}=−\sqrt{\mathrm{5}+{c}} \\ $$$${c}^{\mathrm{4}} −\mathrm{8}{c}^{\mathrm{2}} +\mathrm{16}=\mathrm{5}+{c} \\ $$$${c}^{\mathrm{4}} −\mathrm{8}{c}^{\mathrm{2}} −{c}+\mathrm{11}=\mathrm{0} \\ $$$$\mathrm{Hence}\:\mathrm{c}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to} \\ $$$${y}^{\mathrm{4}} −\mathrm{8}{y}^{\mathrm{2}} −{y}+\mathrm{11}=\mathrm{0} \\ $$

Commented by prakash jain last updated on 30/May/20

eqn1: x^4 −8x^2 +x+11=0 (i) y^4 −8y^2 −y+11=0 (ii) if α is a root of equation (ii) then we can see (−α) will be root of equation (i). so eqn (i) can be written as (x−a)(x−b)(x+c)(x+d)=0 comparing coeffcient of constant term abcd=11

$${eqn}\mathrm{1}: \\ $$$${x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{2}} +{x}+\mathrm{11}=\mathrm{0}\:\left(\mathrm{i}\right) \\ $$$${y}^{\mathrm{4}} −\mathrm{8}{y}^{\mathrm{2}} −{y}+\mathrm{11}=\mathrm{0}\:\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{if}\:\:\alpha\:\mathrm{is}\:\mathrm{a}\:\mathrm{root}\:\mathrm{of}\:\mathrm{equation}\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{see}\:\left(−\alpha\right)\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{root}\:\mathrm{of}\:\mathrm{equation}\:\left(\mathrm{i}\right). \\ $$$$\mathrm{so}\:\mathrm{eqn}\:\left(\mathrm{i}\right)\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$$\left({x}−{a}\right)\left({x}−{b}\right)\left({x}+{c}\right)\left({x}+{d}\right)=\mathrm{0} \\ $$$$\mathrm{comparing}\:\mathrm{coeffcient}\:\mathrm{of}\:\mathrm{constant} \\ $$$$\mathrm{term} \\ $$$${abcd}=\mathrm{11} \\ $$

Commented by mr W last updated on 30/May/20