Question Number 96231 by joki last updated on 30/May/20
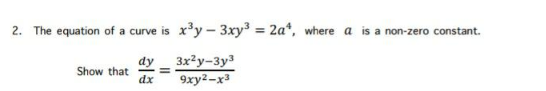
Commented by prakash jain last updated on 30/May/20
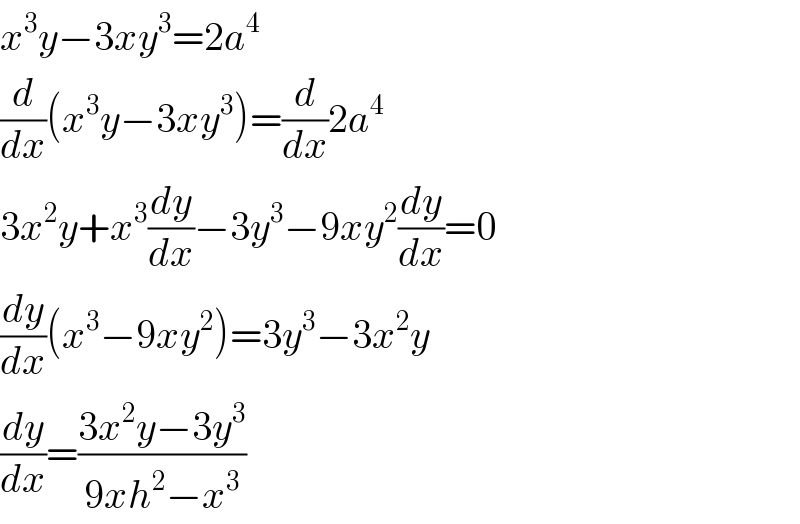
$${x}^{\mathrm{3}} {y}−\mathrm{3}{xy}^{\mathrm{3}} =\mathrm{2}{a}^{\mathrm{4}} \\ $$$$\frac{{d}}{{dx}}\left({x}^{\mathrm{3}} {y}−\mathrm{3}{xy}^{\mathrm{3}} \right)=\frac{{d}}{{dx}}\mathrm{2}{a}^{\mathrm{4}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} {y}+{x}^{\mathrm{3}} \frac{{dy}}{{dx}}−\mathrm{3}{y}^{\mathrm{3}} −\mathrm{9}{xy}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}\left({x}^{\mathrm{3}} −\mathrm{9}{xy}^{\mathrm{2}} \right)=\mathrm{3}{y}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{3}{x}^{\mathrm{2}} {y}−\mathrm{3}{y}^{\mathrm{3}} }{\mathrm{9}{xh}^{\mathrm{2}} −{x}^{\mathrm{3}} } \\ $$
