Question Number 96350 by liki last updated on 31/May/20

Commented by liki last updated on 31/May/20

$$…\mathrm{I}\:\mathrm{need}\:\:\mathrm{help}\:\:\mathrm{please}\:\mathrm{for}\:\mathrm{these}\:\mathrm{question}\:! \\ $$
Commented by bemath last updated on 01/Jun/20
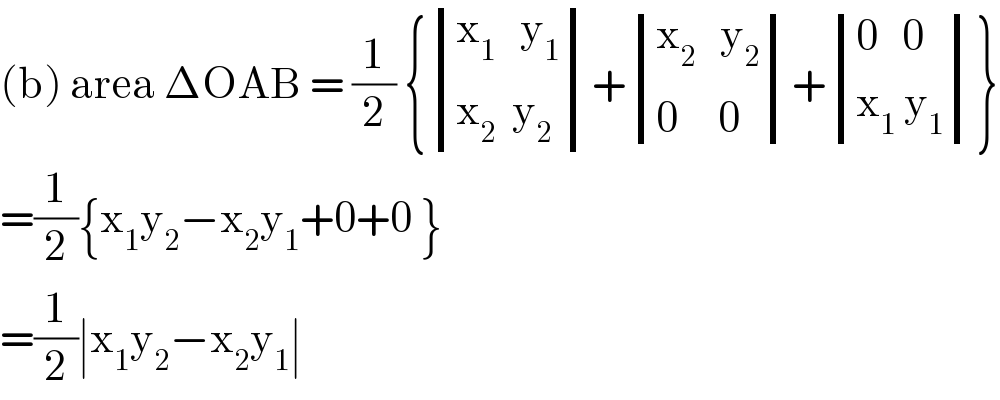
$$\left(\mathrm{b}\right)\:\mathrm{area}\:\Delta\mathrm{OAB}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\begin{vmatrix}{\mathrm{x}_{\mathrm{1}} \:\:\:\mathrm{y}_{\mathrm{1}} }\\{\mathrm{x}_{\mathrm{2}} \:\:\mathrm{y}_{\mathrm{2}} }\end{vmatrix}+\begin{vmatrix}{\mathrm{x}_{\mathrm{2}} \:\:\:\mathrm{y}_{\mathrm{2}} }\\{\mathrm{0}\:\:\:\:\:\mathrm{0}}\end{vmatrix}+\begin{vmatrix}{\mathrm{0}\:\:\:\mathrm{0}}\\{\mathrm{x}_{\mathrm{1}} \:\mathrm{y}_{\mathrm{1}} }\end{vmatrix}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{2}} −\mathrm{x}_{\mathrm{2}} \mathrm{y}_{\mathrm{1}} +\mathrm{0}+\mathrm{0}\:\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{2}} −\mathrm{x}_{\mathrm{2}} \mathrm{y}_{\mathrm{1}} \mid \\ $$
Answered by Rio Michael last updated on 01/Jun/20

$$\left(\mathrm{a}\right)\left(\mathrm{i}\right)\:\mathrm{angle}\:\mathrm{between}\:\mathrm{two}\:\mathrm{lines}\:\mathrm{with}\:\mathrm{gradients}\:{m}_{\mathrm{1}} \:\mathrm{and}\:{m}_{\mathrm{2}} \: \\ $$$$\mathrm{is}\:\mathrm{given}\:\mathrm{by}\:\:\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\:\frac{{m}_{\mathrm{1}} −{m}_{\mathrm{2}} }{\mathrm{1}\:+\:{m}_{\mathrm{1}} {m}_{\mathrm{2}} }\right) \\ $$$${l}_{\mathrm{1}} :\:\:{y}\:=\:−\frac{{ax}}{{b}}\:−\frac{{c}}{{b}}\:\Rightarrow\:{m}_{\mathrm{1}} \:=\:−\frac{{a}}{{b}} \\ $$$${l}_{\mathrm{2}} :\:{y}\:=\:\frac{\left({b}−{a}\right){x}}{\left({a}\:+\:{b}\right)}\:−\frac{{d}}{\left({a}\:+\:{b}\right)}\:\Rightarrow\:{m}_{\mathrm{2}} \:=\:\frac{{b}−{a}}{{a}\:+\:{b}} \\ $$$$\mathrm{tan}\:\theta\:=\:\frac{−\frac{{a}}{{b}}−\frac{{b}−{a}}{{a}\:+{b}}}{\mathrm{1}\:−\left(\frac{{a}}{{b}}\right)\left(\frac{{b}−{a}}{{a}+{b}}\right)}\:=\:\frac{−{a}\left({a}\:+{b}\right)−{b}\left({b}−{a}\right)}{{b}\left({a}\:+\:{b}\right)−{a}\left({b}−{a}\right)}\:=\:\frac{−{a}^{\mathrm{2}} −{ab}−{b}^{\mathrm{2}} \:+{ab}}{{ab}+{b}^{\mathrm{2}} −{ab}+{a}^{\mathrm{2}} }\:=\:−\mathrm{1} \\ $$$$\:\mathrm{tan}\:\theta\:=−\mathrm{1}\:\Rightarrow\:\theta\:=\:−\frac{\pi}{\mathrm{4}}\:\mathrm{or}\:\theta\:=\:\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\:\:\: \\ $$
Commented by liki last updated on 01/Jun/20
$$..\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{sir}};\mathrm{please}\:\mathrm{help}\:\mathrm{others}\:\mathrm{remain} \\ $$
