Menu Close

Question-96428

Tinku Tara 0 Comments
Pin




Question Number 96428 by Hassanfathi last updated on 01/Jun/20
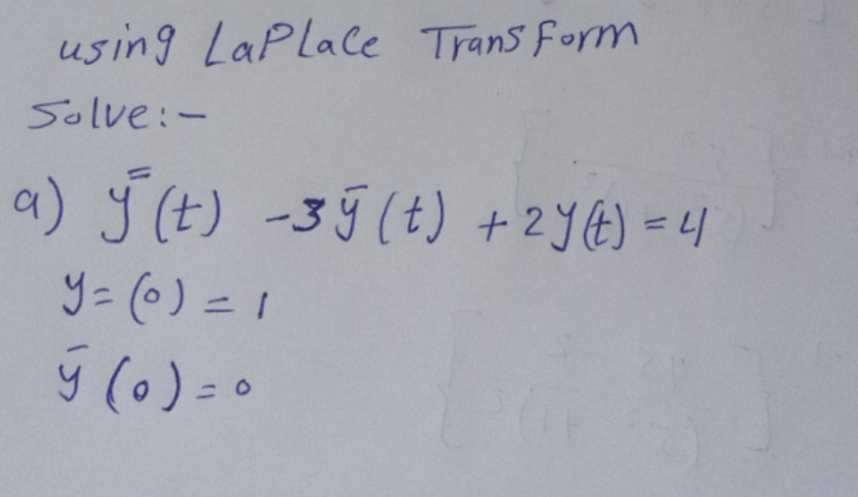
Answered by Sourav mridha last updated on 01/Jun/20
y^(′′) (t)−3y^′ (t)+2y(t)=4 using Laplace transform s^2 y(s)−sy(0)−y^′ (0)−3sy(s)+3y(0) +2y(s)=(4/s) given y(0)=1 and y^′ (0)=0 ⇒y(s)[s^2 −3s+2]=(4/s)+s−3 ⇒y(s)=(([(4/s)+s−3])/((s−2)(s−1))) ⇒L^(−1) [y(s)]=L^(−1) [(4/(s(s−2)(s−1)))+((s−3)/((s−2)(s−1)))] ⇒y(t)=2L^(−1) [(1/s)−(((s−3))/((s−2)(s−1)))] +L^(−1) [(1/(s−1))]−L^(−1) [(1/(s−2))]+L^(−1) [(1/(s−1))] ⇒y(t)=2L^(−1) [(1/s)]−2L^(−1) [(1/((s−1)))] +2L^(−1) [(1/((s−2)))]−2L^(−1) [(1/(s−1))] +2e^t −e^(2t) ⇒y(t)=2−2e^t +e^(2t) ....(Ans)
$$\boldsymbol{{y}}^{''} \left(\boldsymbol{{t}}\right)−\mathrm{3}\boldsymbol{{y}}^{'} \left(\mathrm{t}\right)+\mathrm{2}\boldsymbol{{y}}\left(\boldsymbol{{t}}\right)=\mathrm{4} \\ $$$$\boldsymbol{{using}}\:\boldsymbol{{Laplace}}\:\boldsymbol{{transform}} \\ $$$$\boldsymbol{{s}}^{\mathrm{2}} \boldsymbol{{y}}\left(\boldsymbol{{s}}\right)−\boldsymbol{{sy}}\left(\mathrm{0}\right)−\boldsymbol{{y}}^{'} \left(\mathrm{0}\right)−\mathrm{3}\boldsymbol{{sy}}\left(\boldsymbol{{s}}\right)+\mathrm{3}\boldsymbol{{y}}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{y}}\left(\boldsymbol{{s}}\right)=\frac{\mathrm{4}}{\boldsymbol{{s}}} \\ $$$$\boldsymbol{{given}}\:\boldsymbol{{y}}\left(\mathrm{0}\right)=\mathrm{1}\:\boldsymbol{{and}}\:\boldsymbol{{y}}^{'} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{y}}\left(\boldsymbol{{s}}\right)\left[\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{s}}+\mathrm{2}\right]=\frac{\mathrm{4}}{\boldsymbol{{s}}}+\boldsymbol{{s}}−\mathrm{3} \\ $$$$\Rightarrow\boldsymbol{{y}}\left(\boldsymbol{{s}}\right)=\frac{\left[\frac{\mathrm{4}}{\boldsymbol{{s}}}+\boldsymbol{{s}}−\mathrm{3}\right]}{\left(\boldsymbol{{s}}−\mathrm{2}\right)\left(\boldsymbol{{s}}−\mathrm{1}\right)} \\ $$$$\Rightarrow\boldsymbol{{L}}^{−\mathrm{1}} \left[\mathrm{y}\left(\boldsymbol{{s}}\right)\right]=\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{4}}{\boldsymbol{{s}}\left(\boldsymbol{{s}}−\mathrm{2}\right)\left(\boldsymbol{{s}}−\mathrm{1}\right)}+\frac{\boldsymbol{{s}}−\mathrm{3}}{\left(\boldsymbol{{s}}−\mathrm{2}\right)\left(\boldsymbol{{s}}−\mathrm{1}\right)}\right] \\ $$$$\Rightarrow\boldsymbol{{y}}\left(\boldsymbol{{t}}\right)=\mathrm{2}\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{s}}}−\frac{\left(\boldsymbol{{s}}−\mathrm{3}\right)}{\left(\boldsymbol{{s}}−\mathrm{2}\right)\left(\boldsymbol{{s}}−\mathrm{1}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{s}}−\mathrm{1}}\right]−\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\mathrm{s}−\mathrm{2}}\right]+\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{s}}−\mathrm{1}}\right] \\ $$$$\Rightarrow\boldsymbol{{y}}\left(\boldsymbol{{t}}\right)=\mathrm{2}\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{s}}}\right]−\mathrm{2}\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\left(\boldsymbol{{s}}−\mathrm{1}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\left(\boldsymbol{{s}}−\mathrm{2}\right)}\right]−\mathrm{2}\boldsymbol{{L}}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{s}}−\mathrm{1}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{e}}^{\boldsymbol{{t}}} −\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} \\ $$$$\Rightarrow\boldsymbol{{y}}\left(\boldsymbol{{t}}\right)=\mathrm{2}−\mathrm{2}\boldsymbol{{e}}^{\boldsymbol{{t}}} +\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} ….\left(\boldsymbol{{Ans}}\right) \\ $$
Answered by mathmax by abdo last updated on 01/Jun/20
y^(′′) (t)−3y^′ (t)+2y(t) =4 ⇒L(y^(′′) )−3L(y^′ )+2L(y) =(4/t) ⇒ t^2 L(y)−ty(0)−y^′ (0)−3(tL(y)−y(o))+2L(y) =(4/t) ⇒ (t^2 −3t +2)L(y) =(4/t) +ty(0)+y^′ (0)−3y(0) ⇒ (t^2 −3t+2)L(y) =(4/t) +t−3 ⇒L(y) =(4/(t(t^2 −3t +2))) +((t−3)/(t^2 −3t +2)) ⇒ y =4L^(−1) ((1/(t(t^2 −3t+2))))+L^(−1) (((t−3)/(t^2 −3t +2))) f(t) =((t−3)/(t^2 −3t +2)) =((t−3)/(t^2 −t−2(t−1))) =((t−3)/(t(t−1)−2(t−1))) =((t−3)/((t−1)(t−2))) =(a/(t−1)) +(b/(t−2)) ⇒a =((−2)/(−1)) =2 , b =((−1)/1) =−1 ⇒f(t) =(2/(t−1))−(1/(t−2)) ⇒ L^(−1) (f(x)) =2e^t −e^(2t) g(t) =(1/(t(t^2 −3t +2))) =(1/(t(t−1)(t−2))) =(a/t) +(b/(t−1)) +(c/(t−2)) a =(1/2) , b =−1 , c =(1/2) ⇒g(t) =(1/(2t))−(1/(t−1)) +(1/(2(t−2))) ⇒ L^(−1) (g(t)) =(1/2) −e^t +(1/2)e^(2t) ⇒y =2 −4e^t +2e^(2t) +2e^t −e^(2t) ⇒ y(t) =e^(2t) −2e^t +2
$$\mathrm{y}^{''} \left(\mathrm{t}\right)−\mathrm{3y}^{'} \left(\mathrm{t}\right)+\mathrm{2y}\left(\mathrm{t}\right)\:=\mathrm{4}\:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)−\mathrm{3L}\left(\mathrm{y}^{'} \right)+\mathrm{2L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4}}{\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{t}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{ty}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)−\mathrm{3}\left(\mathrm{tL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{o}\right)\right)+\mathrm{2L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4}}{\mathrm{t}}\:\Rightarrow \\ $$$$\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4}}{\mathrm{t}}\:+\mathrm{ty}\left(\mathrm{0}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)−\mathrm{3y}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4}}{\mathrm{t}}\:+\mathrm{t}−\mathrm{3}\:\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{4}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}\right)}\:+\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{4L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{2}\right)}\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}}\right) \\ $$$$\mathrm{f}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}}\:=\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}−\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}\:=\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}\left(\mathrm{t}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}\:=\frac{\mathrm{t}−\mathrm{3}}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}−\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{2}}\:\Rightarrow\mathrm{a}\:=\frac{−\mathrm{2}}{−\mathrm{1}}\:=\mathrm{2}\:\:,\:\:\mathrm{b}\:=\frac{−\mathrm{1}}{\mathrm{1}}\:=−\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)\:=\frac{\mathrm{2}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\mathrm{2e}^{\mathrm{t}} −\mathrm{e}^{\mathrm{2t}} \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}\:+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}−\mathrm{2}\right)}\:=\frac{\mathrm{a}}{\mathrm{t}}\:+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{1}}\:+\frac{\mathrm{c}}{\mathrm{t}−\mathrm{2}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\:,\:\mathrm{b}\:=−\mathrm{1}\:\:,\:\:\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\mathrm{2t}}−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}−\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{g}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{e}^{\mathrm{t}} \:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2t}} \:\Rightarrow\mathrm{y}\:=\mathrm{2}\:−\mathrm{4e}^{\mathrm{t}} \:+\mathrm{2e}^{\mathrm{2t}} \:\:+\mathrm{2e}^{\mathrm{t}} −\mathrm{e}^{\mathrm{2t}} \:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{t}\right)\:=\mathrm{e}^{\mathrm{2t}} \:−\mathrm{2e}^{\mathrm{t}} \:+\mathrm{2}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *