Question Number 96497 by Fikret last updated on 02/Jun/20
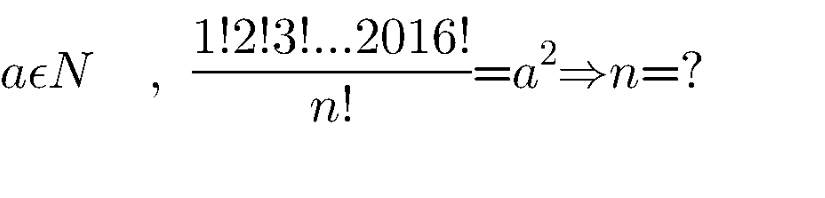
Answered by Farruxjano last updated on 02/Jun/20
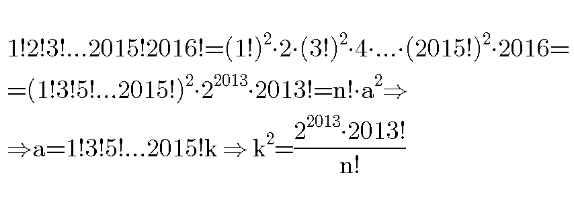
Commented by prakash jain last updated on 02/Jun/20
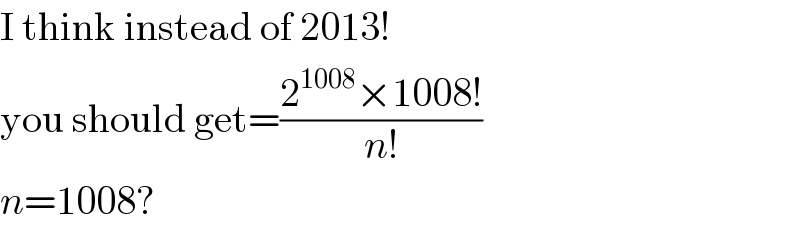
$$\mathrm{I}\:\mathrm{think}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{2013}! \\ $$$$\mathrm{you}\:\mathrm{should}\:\mathrm{get}=\frac{\mathrm{2}^{\mathrm{1008}} ×\mathrm{1008}!}{{n}!} \\ $$$${n}=\mathrm{1008}? \\ $$
Commented by Farruxjano last updated on 02/Jun/20
$$\mathrm{Oh},\:\mathrm{yes}\:\mathrm{you}'\mathrm{re}\:\mathrm{right}!\:\mathrm{Sorrt}\:\mathrm{for}\:\mathrm{the}\:\mathrm{simple}\:\mathrm{mistake} \\ $$
Answered by Farruxjano last updated on 02/Jun/20
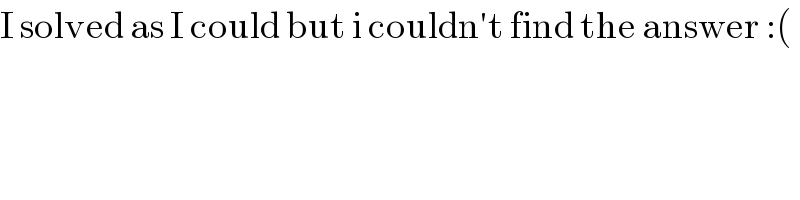
$$\mathrm{I}\:\mathrm{solved}\:\mathrm{as}\:\mathrm{I}\:\mathrm{could}\:\mathrm{but}\:\mathrm{i}\:\mathrm{couldn}'\mathrm{t}\:\mathrm{find}\:\mathrm{the}\:\mathrm{answer}\::\left(\right. \\ $$
