Menu Close

Question-96584

Tinku Tara 0 Comments
Pin




Question Number 96584 by Jidda28 last updated on 04/Jun/20
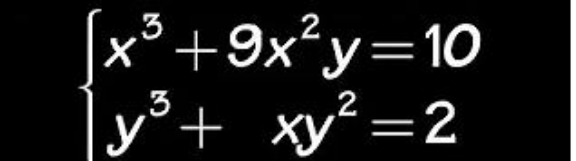
Commented by mr W last updated on 03/Jun/20
when posting an image you should crop the image properly or diasable crop.
$${when}\:{posting}\:{an}\:{image}\:{you}\:{should} \\ $$$${crop}\:{the}\:{image}\:{properly}\:{or}\:{diasable} \\ $$$${crop}. \\ $$
Commented by prakash jain last updated on 04/Jun/20
Hi Please move/resize black rectangle to select appropriate crop area. If you wish to upload entire image. Just disable crop.
$$\mathrm{Hi} \\ $$$$\mathrm{Please}\:\mathrm{move}/\mathrm{resize}\:\mathrm{black}\:\mathrm{rectangle} \\ $$$$\mathrm{to}\:\mathrm{select}\:\mathrm{appropriate}\:\mathrm{crop}\:\mathrm{area}. \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{wish}\:\mathrm{to}\:\mathrm{upload}\:\mathrm{entire}\:\mathrm{image}. \\ $$$$\mathrm{Just}\:\mathrm{disable}\:\mathrm{crop}. \\ $$
Commented by Jidda28 last updated on 04/Jun/20
ok sir i edited the post.
$$\mathrm{ok}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{edited}\:\mathrm{the}\:\mathrm{post}. \\ $$
Commented by Jidda28 last updated on 04/Jun/20
ok sir i edited the post.
$$\mathrm{ok}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{edited}\:\mathrm{the}\:\mathrm{post}. \\ $$
Answered by prakash jain last updated on 04/Jun/20
y^3 +xy^2 =2 x=((2−y^3 )/y^2 ) (((2−y^3 )/y^2 ))^3 +9y(((2−y^3 )/y^2 ))^2 =10 ((2/y^2 )−y)^3 +9y((2/y^2 )−y)^2 =10 −y^3 +6−((12)/y^3 )+(8/y^6 )+((36)/y^3 )+9y^3 −36=10 8y^3 −30+((24)/y^3 )+(8/y^6 )=10 8y^3 −40+((24)/y^3 )+(8/y^6 )=10 y^3 −5+(3/y^3 )+(1/y^6 )=0 y^3 =u u−5+(3/u)+(1/u^2 )=0 u^3 −5u^2 +3u+1=0 u^3 −u^2 −4u^2 +4u−u+1=0 u^2 (u−1)−4u(u−1)−(u−1)=9 (u−1)(u^2 −4u−1)=0 (I) u=1 u=((4±(√(20)))/2)=2±(√5) Considering only real roots u=y^3 =1⇒y=1 u=y^3 =2±(√5) =((1/2)(1±(√5)))^3 ⇒y=((1±(√5))/2) x=((2−y^3 )/y^2 ) y=1⇒x=1 y=((1±(√5))/2)⇒x=((2−(2±(√5)))/((1/4)(1±(√5))^2 ))=((∓4(√5))/(6±2(√5))) x=((∓4(√5)(6∓2(√5)))/(6^2 −20))=(1/2)(5∓3(√5)) If you need you can calculate complex roots from (I)
$${y}^{\mathrm{3}} +{xy}^{\mathrm{2}} =\mathrm{2} \\ $$$${x}=\frac{\mathrm{2}−{y}^{\mathrm{3}} }{{y}^{\mathrm{2}} } \\ $$$$\left(\frac{\mathrm{2}−{y}^{\mathrm{3}} }{{y}^{\mathrm{2}} }\right)^{\mathrm{3}} +\mathrm{9}{y}\left(\frac{\mathrm{2}−{y}^{\mathrm{3}} }{{y}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{10} \\ $$$$\left(\frac{\mathrm{2}}{{y}^{\mathrm{2}} }−{y}\right)^{\mathrm{3}} +\mathrm{9}{y}\left(\frac{\mathrm{2}}{{y}^{\mathrm{2}} }−{y}\right)^{\mathrm{2}} =\mathrm{10} \\ $$$$−{y}^{\mathrm{3}} +\mathrm{6}−\frac{\mathrm{12}}{{y}^{\mathrm{3}} }+\frac{\mathrm{8}}{{y}^{\mathrm{6}} }+\frac{\mathrm{36}}{{y}^{\mathrm{3}} }+\mathrm{9}{y}^{\mathrm{3}} −\mathrm{36}=\mathrm{10} \\ $$$$\mathrm{8}{y}^{\mathrm{3}} −\mathrm{30}+\frac{\mathrm{24}}{{y}^{\mathrm{3}} }+\frac{\mathrm{8}}{{y}^{\mathrm{6}} }=\mathrm{10} \\ $$$$\mathrm{8}{y}^{\mathrm{3}} −\mathrm{40}+\frac{\mathrm{24}}{{y}^{\mathrm{3}} }+\frac{\mathrm{8}}{{y}^{\mathrm{6}} }=\mathrm{10} \\ $$$${y}^{\mathrm{3}} −\mathrm{5}+\frac{\mathrm{3}}{{y}^{\mathrm{3}} }+\frac{\mathrm{1}}{{y}^{\mathrm{6}} }=\mathrm{0} \\ $$$${y}^{\mathrm{3}} ={u} \\ $$$${u}−\mathrm{5}+\frac{\mathrm{3}}{{u}}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }=\mathrm{0} \\ $$$${u}^{\mathrm{3}} −\mathrm{5}{u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{1}=\mathrm{0} \\ $$$${u}^{\mathrm{3}} −{u}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} +\mathrm{4}{u}−{u}+\mathrm{1}=\mathrm{0} \\ $$$${u}^{\mathrm{2}} \left({u}−\mathrm{1}\right)−\mathrm{4}{u}\left({u}−\mathrm{1}\right)−\left({u}−\mathrm{1}\right)=\mathrm{9} \\ $$$$\left({u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} −\mathrm{4}{u}−\mathrm{1}\right)=\mathrm{0}\:\:\:\:\left(\mathrm{I}\right) \\ $$$${u}=\mathrm{1} \\ $$$${u}=\frac{\mathrm{4}\pm\sqrt{\mathrm{20}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{5}} \\ $$$$\mathrm{Considering}\:\mathrm{only}\:\mathrm{real}\:\mathrm{roots} \\ $$$${u}={y}^{\mathrm{3}} =\mathrm{1}\Rightarrow{y}=\mathrm{1} \\ $$$${u}={y}^{\mathrm{3}} =\mathrm{2}\pm\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\pm\sqrt{\mathrm{5}}\right)\right)^{\mathrm{3}} \Rightarrow{y}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{2}−{y}^{\mathrm{3}} }{{y}^{\mathrm{2}} } \\ $$$${y}=\mathrm{1}\Rightarrow{x}=\mathrm{1} \\ $$$${y}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow{x}=\frac{\mathrm{2}−\left(\mathrm{2}\pm\sqrt{\mathrm{5}}\right)}{\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}\pm\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mp\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{6}\pm\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${x}=\frac{\mp\mathrm{4}\sqrt{\mathrm{5}}\left(\mathrm{6}\mp\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{6}^{\mathrm{2}} −\mathrm{20}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}\mp\mathrm{3}\sqrt{\mathrm{5}}\right) \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{need}\:\mathrm{you}\:\mathrm{can}\:\mathrm{calculate} \\ $$$$\mathrm{complex}\:\mathrm{roots}\:\mathrm{from}\:\left(\mathrm{I}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *