Question Number 96671 by 175 last updated on 03/Jun/20

Answered by maths mind last updated on 03/Jun/20
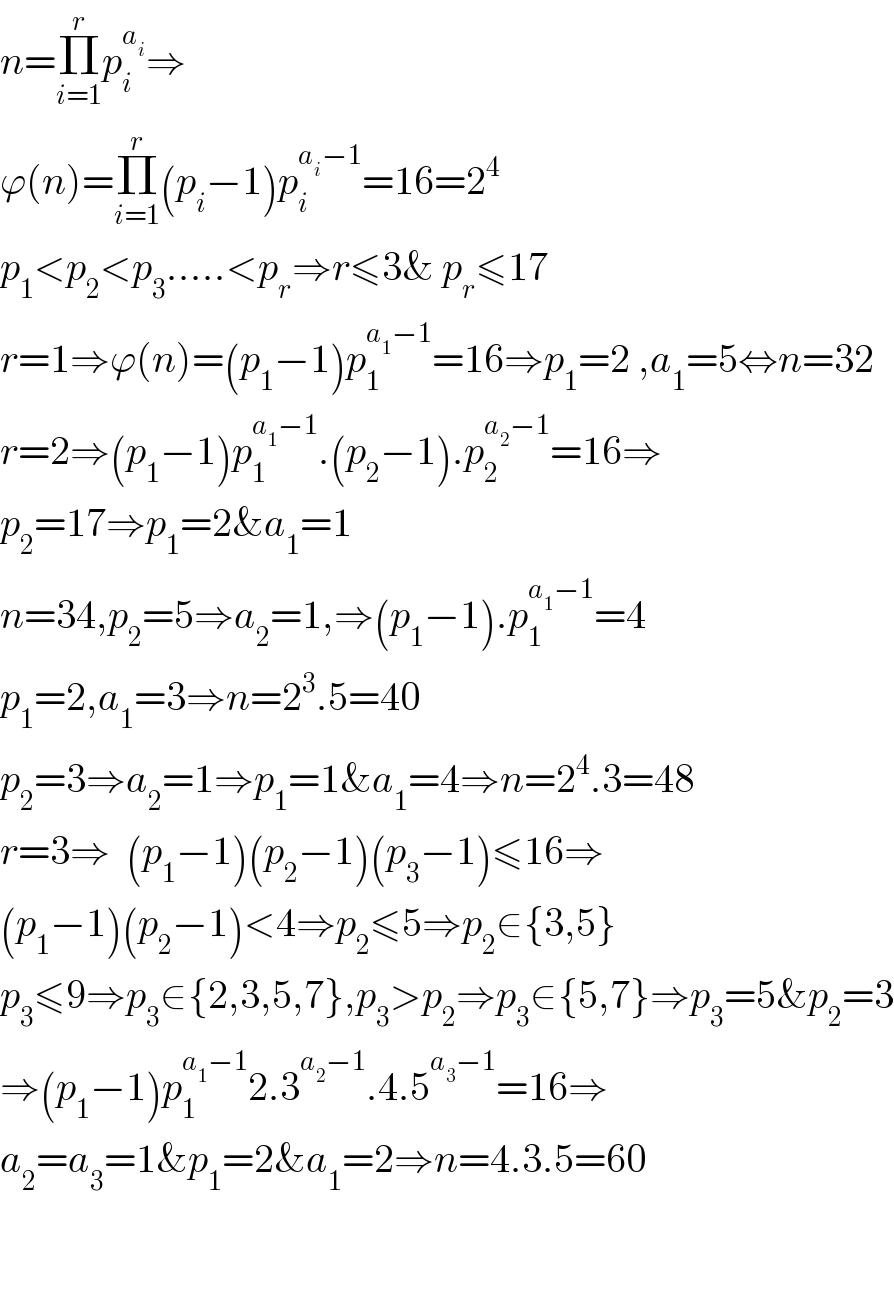
$${n}=\underset{{i}=\mathrm{1}} {\overset{{r}} {\prod}}{p}_{{i}} ^{{a}_{{i}} } \Rightarrow \\ $$$$\varphi\left({n}\right)=\underset{{i}=\mathrm{1}} {\overset{{r}} {\prod}}\left({p}_{{i}} −\mathrm{1}\right){p}_{{i}} ^{{a}_{{i}} −\mathrm{1}} =\mathrm{16}=\mathrm{2}^{\mathrm{4}} \\ $$$${p}_{\mathrm{1}} <{p}_{\mathrm{2}} <{p}_{\mathrm{3}} …..<{p}_{{r}} \Rightarrow{r}\leqslant\mathrm{3\&}\:{p}_{{r}} \leqslant\mathrm{17} \\ $$$${r}=\mathrm{1}\Rightarrow\varphi\left({n}\right)=\left({p}_{\mathrm{1}} −\mathrm{1}\right){p}_{\mathrm{1}} ^{{a}_{\mathrm{1}} −\mathrm{1}} =\mathrm{16}\Rightarrow{p}_{\mathrm{1}} =\mathrm{2}\:,{a}_{\mathrm{1}} =\mathrm{5}\Leftrightarrow{n}=\mathrm{32} \\ $$$${r}=\mathrm{2}\Rightarrow\left({p}_{\mathrm{1}} −\mathrm{1}\right){p}_{\mathrm{1}} ^{{a}_{\mathrm{1}} −\mathrm{1}} .\left({p}_{\mathrm{2}} −\mathrm{1}\right).{p}_{\mathrm{2}} ^{{a}_{\mathrm{2}} −\mathrm{1}} =\mathrm{16}\Rightarrow \\ $$$${p}_{\mathrm{2}} =\mathrm{17}\Rightarrow{p}_{\mathrm{1}} =\mathrm{2\&}{a}_{\mathrm{1}} =\mathrm{1} \\ $$$${n}=\mathrm{34},{p}_{\mathrm{2}} =\mathrm{5}\Rightarrow{a}_{\mathrm{2}} =\mathrm{1},\Rightarrow\left({p}_{\mathrm{1}} −\mathrm{1}\right).{p}_{\mathrm{1}} ^{{a}_{\mathrm{1}} −\mathrm{1}} =\mathrm{4} \\ $$$${p}_{\mathrm{1}} =\mathrm{2},{a}_{\mathrm{1}} =\mathrm{3}\Rightarrow{n}=\mathrm{2}^{\mathrm{3}} .\mathrm{5}=\mathrm{40} \\ $$$${p}_{\mathrm{2}} =\mathrm{3}\Rightarrow{a}_{\mathrm{2}} =\mathrm{1}\Rightarrow{p}_{\mathrm{1}} =\mathrm{1\&}{a}_{\mathrm{1}} =\mathrm{4}\Rightarrow{n}=\mathrm{2}^{\mathrm{4}} .\mathrm{3}=\mathrm{48} \\ $$$${r}=\mathrm{3}\Rightarrow\:\:\left({p}_{\mathrm{1}} −\mathrm{1}\right)\left({p}_{\mathrm{2}} −\mathrm{1}\right)\left({p}_{\mathrm{3}} −\mathrm{1}\right)\leqslant\mathrm{16}\Rightarrow \\ $$$$\left({p}_{\mathrm{1}} −\mathrm{1}\right)\left({p}_{\mathrm{2}} −\mathrm{1}\right)<\mathrm{4}\Rightarrow{p}_{\mathrm{2}} \leqslant\mathrm{5}\Rightarrow{p}_{\mathrm{2}} \in\left\{\mathrm{3},\mathrm{5}\right\} \\ $$$${p}_{\mathrm{3}} \leqslant\mathrm{9}\Rightarrow{p}_{\mathrm{3}} \in\left\{\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7}\right\},{p}_{\mathrm{3}} >{p}_{\mathrm{2}} \Rightarrow{p}_{\mathrm{3}} \in\left\{\mathrm{5},\mathrm{7}\right\}\Rightarrow{p}_{\mathrm{3}} =\mathrm{5\&}{p}_{\mathrm{2}} =\mathrm{3} \\ $$$$\Rightarrow\left({p}_{\mathrm{1}} −\mathrm{1}\right){p}_{\mathrm{1}} ^{{a}_{\mathrm{1}} −\mathrm{1}} \mathrm{2}.\mathrm{3}^{{a}_{\mathrm{2}} −\mathrm{1}} .\mathrm{4}.\mathrm{5}^{{a}_{\mathrm{3}} −\mathrm{1}} =\mathrm{16}\Rightarrow \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{3}} =\mathrm{1\&}{p}_{\mathrm{1}} =\mathrm{2\&}{a}_{\mathrm{1}} =\mathrm{2}\Rightarrow{n}=\mathrm{4}.\mathrm{3}.\mathrm{5}=\mathrm{60} \\ $$$$ \\ $$$$ \\ $$
Commented by 175 last updated on 04/Jun/20
nice job
