Question Number 96693 by 175 last updated on 03/Jun/20
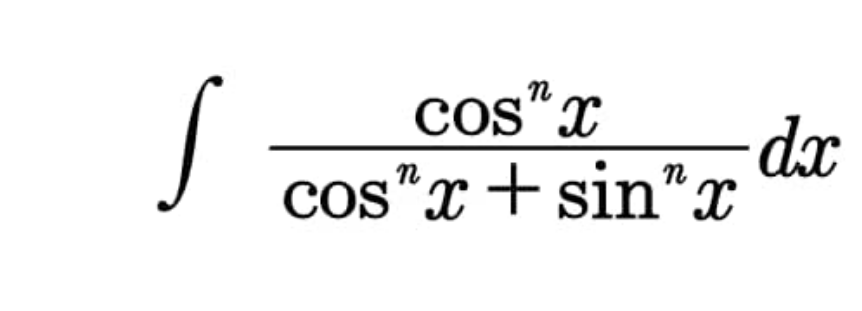
Answered by abdomathmax last updated on 04/Jun/20
![A_n =∫ (dx/(1+tan^n x)) =_(tanx =t) ∫ (dt/((1+t^2 )(1+t^n ))) let decompose F(t) =(1/((t^2 +1)(t^n +1))) =(1/((t−i(t+i)(t^n +1))) ⇒F(t) =(a/(t−i)) +(b/(t+i)) +Σ_(p=0) ^(n−1) (a_p /(t−z_p )) z_p roots of t^n +1=0 ⇒z_p =e^(i(((2k+1)π)/p)) p ∈[[0,n−1]] a =(1/(2i(1+i^n ))) and b =((−1)/(2i(1+(−i)^n ))) ⇒ F(t)=(1/(2i(i^n +1)(t−i))) −(1/(2i(1+(−i)^n )(t+i))) +Σ_(p=0) ^(n−1) (a_p /(t−z_p )) =(1/(2i)){(((1+(−i)^n )(t+i)−(1+i^n )(t−i))/((1+i^n )(1+(−1)^n )(t^2 +1)))} +Σ_(p=0) ^(n−1) (a_p /(t−z_p )) =((αt +β)/(t^2 +1)) +Σ_(p=0) ^(n−1) (a_p /(t−z_p )) ⇒ (1/((t^2 +1)(t^n +1)))−((αt+β)/(t^2 +1)) =Σ_(p=0) ^(n−1) (a_p /(t−z_p )) ⇒ (1/((t^2 +1))){(1/(t^n +1))−(αt +β)} =Σ(...) ⇒ ((1−(αt +β)(t^n +1))/((t^2 +1)(t^n +1))) =Σ_(p=0) ^∞ (a_p /(t−z_p )) a_p =((f(z_(p)) )/(g^′ (z_p ))) we have f(z_p ) =((1−(αz_p +β)(z_p ^n +1))/((z_p ^2 +1)(z_p ^n +1))) g(t) =t^(n+2) +t^2 +t^n +1 ⇒ g^′ (t) =(n+2)t^(n+1) +nt^(n−1) +2t ⇒ g^′ (z_p ) =(n+2)z_p ^(n+1) +nz_p ^(n−1) +2z_p ⇒ ∫ F(t)dt =aln(t−i)+bln(t+i)+Σ_(p=0) ^(n−1) a_p ln(t−z_p ) +C](https://www.tinkutara.com/question/Q96750.png)
$$\mathrm{A}_{\mathrm{n}} =\int\:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{n}} \mathrm{x}}\:=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\:\:\int\:\:\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{n}} \right)} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{t}−\mathrm{i}\left(\mathrm{t}+\mathrm{i}\right)\left(\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\right)\right.} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{i}}\:+\frac{\mathrm{b}}{\mathrm{t}+\mathrm{i}}\:+\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} } \\ $$$$\mathrm{z}_{\mathrm{p}} \:\mathrm{roots}\:\mathrm{of}\:\:\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{z}_{\mathrm{p}} =\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{p}}} \:\:\mathrm{p}\:\in\left[\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right] \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2i}\left(\mathrm{1}+\mathrm{i}^{\mathrm{n}} \right)}\:\mathrm{and}\:\mathrm{b}\:=\frac{−\mathrm{1}}{\mathrm{2i}\left(\mathrm{1}+\left(−\mathrm{i}\right)^{\mathrm{n}} \right)}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2i}\left(\mathrm{i}^{\mathrm{n}} +\mathrm{1}\right)\left(\mathrm{t}−\mathrm{i}\right)}\:−\frac{\mathrm{1}}{\mathrm{2i}\left(\mathrm{1}+\left(−\mathrm{i}\right)^{\mathrm{n}} \right)\left(\mathrm{t}+\mathrm{i}\right)}\:+\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\left\{\frac{\left(\mathrm{1}+\left(−\mathrm{i}\right)^{\mathrm{n}} \right)\left(\mathrm{t}+\mathrm{i}\right)−\left(\mathrm{1}+\mathrm{i}^{\mathrm{n}} \right)\left(\mathrm{t}−\mathrm{i}\right)}{\left(\mathrm{1}+\mathrm{i}^{\mathrm{n}} \right)\left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\right\} \\ $$$$+\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} } \\ $$$$=\frac{\alpha\mathrm{t}\:+\beta}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\right)}−\frac{\alpha\mathrm{t}+\beta}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\left\{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{n}} +\mathrm{1}}−\left(\alpha\mathrm{t}\:+\beta\right)\right\}\:=\Sigma\left(…\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}−\left(\alpha\mathrm{t}\:+\beta\right)\left(\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\right)}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\right)}\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{a}_{\mathrm{p}} }{\mathrm{t}−\mathrm{z}_{\mathrm{p}} } \\ $$$$\mathrm{a}_{\mathrm{p}} =\frac{\mathrm{f}\left(\mathrm{z}_{\left.\mathrm{p}\right)} \right.}{\mathrm{g}^{'} \left(\mathrm{z}_{\mathrm{p}} \right)}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{z}_{\mathrm{p}} \right)\:=\frac{\mathrm{1}−\left(\alpha\mathrm{z}_{\mathrm{p}} +\beta\right)\left(\mathrm{z}_{\mathrm{p}} ^{\mathrm{n}} \:+\mathrm{1}\right)}{\left(\mathrm{z}_{\mathrm{p}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{z}_{\mathrm{p}} ^{\mathrm{n}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\:=\mathrm{t}^{\mathrm{n}+\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{n}} \:+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{t}\right)\:=\left(\mathrm{n}+\mathrm{2}\right)\mathrm{t}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{nt}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{2t}\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{z}_{\mathrm{p}} \right)\:=\left(\mathrm{n}+\mathrm{2}\right)\mathrm{z}_{\mathrm{p}} ^{\mathrm{n}+\mathrm{1}} \:+\mathrm{nz}_{\mathrm{p}} ^{\mathrm{n}−\mathrm{1}} \:+\mathrm{2z}_{\mathrm{p}} \:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{aln}\left(\mathrm{t}−\mathrm{i}\right)+\mathrm{bln}\left(\mathrm{t}+\mathrm{i}\right)+\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{a}_{\mathrm{p}} \mathrm{ln}\left(\mathrm{t}−\mathrm{z}_{\mathrm{p}} \right)\:+\mathrm{C} \\ $$$$ \\ $$
Commented by 175 last updated on 04/Jun/20
nice
Commented by mathmax by abdo last updated on 04/Jun/20

$$\mathrm{thankx} \\ $$
