Question-96936

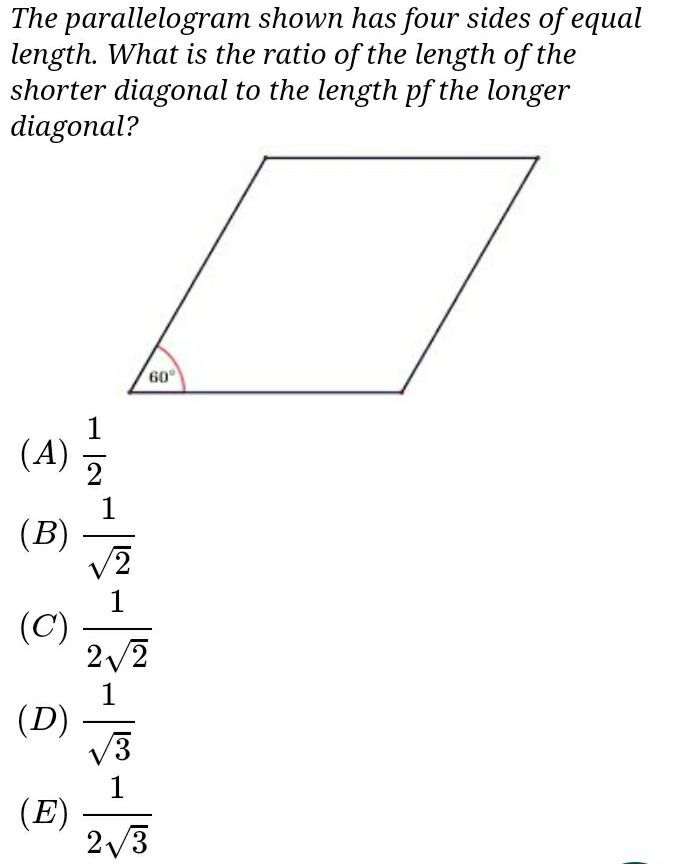
Question Number 96936 by joki last updated on 05/Jun/20

Commented by PRITHWISH SEN 2 last updated on 05/Jun/20

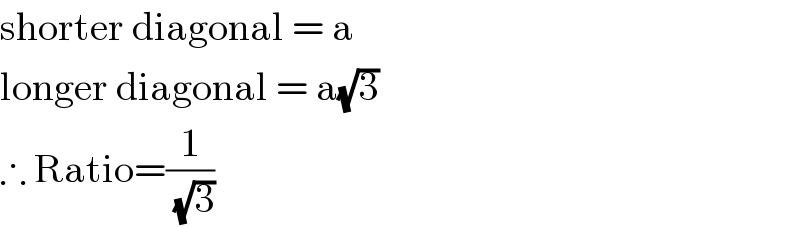
shorter diagonal = a longer diagonal = a(√3) ∴ Ratio=(1/( (√3)))

$$\mathrm{shorter}\:\mathrm{diagonal}\:=\:\mathrm{a} \\ $$$$\mathrm{longer}\:\mathrm{diagonal}\:=\:\mathrm{a}\sqrt{\mathrm{3}} \\ $$$$\therefore\:\mathrm{Ratio}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$

Answered by 1549442205 last updated on 05/Jun/20

Denote by a the length of the side of parallelogram.Then the length of shorter diagonal is equal to a (since it is a side of the regular triangle.The length of longer diagonal equal to two times the length of altitude of regular triangle i.e it is equal to a(√3).Thus,(d_(sh) /d_l )=(a/(a(√3)))=(1/( (√3))).Hence,choose D is the answer

$$\mathrm{Denote}\:\mathrm{by}\:\mathrm{a}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{parallelogram}.\mathrm{Then} \\ $$$$\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{shorter}\:\mathrm{diagonal}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{a} \\ $$$$\left(\mathrm{since}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{side}\:\mathrm{of}\:\:\mathrm{the}\:\mathrm{regular}\:\mathrm{triangle}.\mathrm{The}\:\mathrm{length}\right. \\ $$$$\mathrm{of}\:\mathrm{longer}\:\mathrm{diagonal}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{two}\:\mathrm{times}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of} \\ $$$$\mathrm{altitude}\:\mathrm{of}\:\mathrm{regular}\:\mathrm{triangle}\:\mathrm{i}.\mathrm{e}\:\mathrm{it}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{a}\sqrt{\mathrm{3}}.\mathrm{Thus},\frac{\mathrm{d}_{\mathrm{sh}} }{\mathrm{d}_{\mathrm{l}} }=\frac{\mathrm{a}}{\mathrm{a}\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}.\mathrm{Hence},\mathrm{choose}\:\mathrm{D}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{answer}\: \\ $$

Answered by bobhans last updated on 06/Jun/20

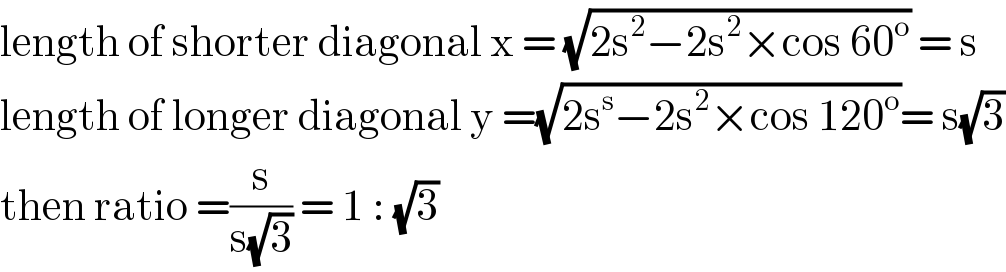
length of shorter diagonal x = (√(2s^2 −2s^2 ×cos 60^o )) = s length of longer diagonal y =(√(2s^s −2s^2 ×cos 120^o ))= s(√3) then ratio =(s/(s(√3))) = 1 : (√3)

$$\mathrm{length}\:\mathrm{of}\:\mathrm{shorter}\:\mathrm{diagonal}\:\mathrm{x}\:=\:\sqrt{\mathrm{2s}^{\mathrm{2}} −\mathrm{2s}^{\mathrm{2}} ×\mathrm{cos}\:\mathrm{60}^{\mathrm{o}} }\:=\:\mathrm{s} \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{longer}\:\mathrm{diagonal}\:\mathrm{y}\:=\sqrt{\mathrm{2s}^{\mathrm{s}} −\mathrm{2s}^{\mathrm{2}} ×\mathrm{cos}\:\mathrm{120}^{\mathrm{o}} }=\:\mathrm{s}\sqrt{\mathrm{3}} \\ $$$$\mathrm{then}\:\mathrm{ratio}\:=\frac{\mathrm{s}}{\mathrm{s}\sqrt{\mathrm{3}}}\:=\:\mathrm{1}\::\:\sqrt{\mathrm{3}}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply