Question Number 96947 by RAMANA last updated on 05/Jun/20

Commented by PRITHWISH SEN 2 last updated on 05/Jun/20
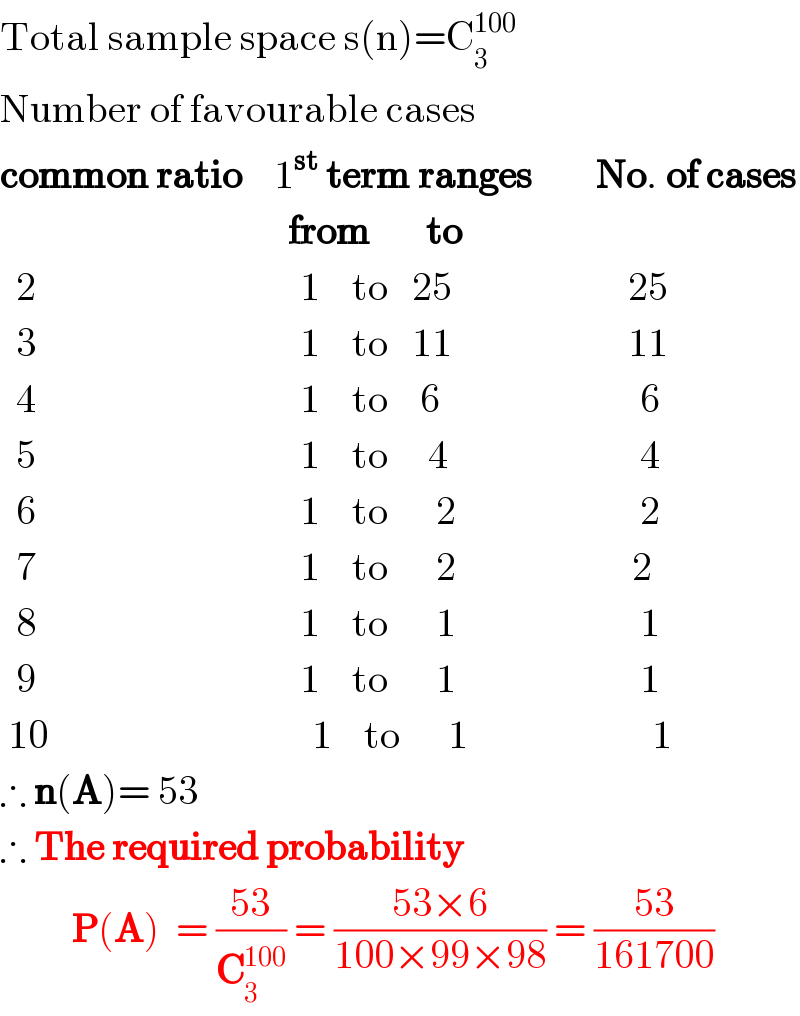
$$\mathrm{Total}\:\mathrm{sample}\:\mathrm{space}\:\mathrm{s}\left(\mathrm{n}\right)=\mathrm{C}_{\mathrm{3}} ^{\mathrm{100}} \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{favourable}\:\mathrm{cases} \\ $$$$\boldsymbol{\mathrm{common}}\:\boldsymbol{\mathrm{ratio}}\:\:\:\:\mathrm{1}^{\boldsymbol{\mathrm{st}}} \:\boldsymbol{\mathrm{term}}\:\boldsymbol{\mathrm{ranges}}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{No}}.\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{cases}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{from}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{to}} \\ $$$$\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\mathrm{25}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{25} \\ $$$$\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\mathrm{11}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{11} \\ $$$$\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6} \\ $$$$\:\:\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4} \\ $$$$\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2} \\ $$$$\:\:\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2} \\ $$$$\:\:\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\:\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\mathrm{10}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{to}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\therefore\:\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{A}}\right)=\:\mathrm{53} \\ $$$$\therefore\:\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{required}}\:\boldsymbol{\mathrm{probability}} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{P}}\left(\boldsymbol{\mathrm{A}}\right)\:\:=\:\frac{\mathrm{53}}{\boldsymbol{\mathrm{C}}_{\mathrm{3}} ^{\mathrm{100}} }\:=\:\frac{\mathrm{53}×\mathrm{6}}{\mathrm{100}×\mathrm{99}×\mathrm{98}}\:=\:\frac{\mathrm{53}}{\mathrm{161700}} \\ $$
Commented by RAMANA last updated on 05/Jun/20
$$\mathrm{welldone}..\:\mathrm{Thanks}\:\mathrm{sir}.. \\ $$
Commented by 1549442205 last updated on 06/Jun/20

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:''\mathrm{GP}''\:\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}? \\ $$$$\:\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{clearly}? \\ $$
Commented by RAMANA last updated on 07/Jun/20
$$\mathrm{It}\:\mathrm{is}\:\mathrm{Geometric}\:\mathrm{progression} \\ $$
