Menu Close

Question-97005

Tinku Tara 0 Comments
Pin




Question Number 97005 by PRITHWISH SEN 2 last updated on 06/Jun/20
Commented by malwaan last updated on 06/Jun/20
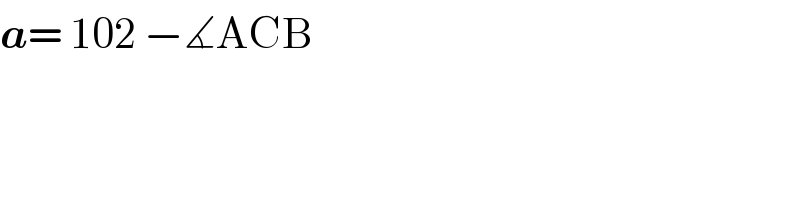
a= 102 −∡ACB
$$\boldsymbol{{a}}=\:\mathrm{102}\:−\measuredangle\mathrm{ACB} \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
I think some information is missing. I want your sugestions.
$$\mathrm{I}\:\mathrm{think}\:\mathrm{some}\:\mathrm{information}\:\mathrm{is}\:\mathrm{missing}.\:\mathrm{I}\:\mathrm{want}\:\mathrm{your} \\ $$$$\mathrm{sugestions}. \\ $$
Answered by mr W last updated on 06/Jun/20
Commented by mr W last updated on 06/Jun/20
say AD=1 AB=BD=(1/(2 cos 72)) ((AD)/(sin 66))=((CD)/(sin 30)) ⇒CD=((AD sin 30)/(sin 66))=(1/(2 sin 66)) BC=(√(CD^2 +BD^2 −2×CD×BD×cos 12)) BC=(√((1/(4 sin^2 66))+(1/(4 cos^2 72))−((cos 12)/(2 sin 66 cos 72)))) ((sin α)/(CD))=((sin 12)/(BC)) sin α=((CD sin 12)/(BC)) =((sin 12)/(2 sin 66 (√((1/(4 sin^2 66))+(1/(4 cos^2 72))−((cos 12)/(2 sin 66 cos 72)))))) =((sin 12)/( (√(1+((sin^2 66)/(cos^2 72))−((2 sin 66 cos 12)/(cos 72)))))) α=sin^(−1) ((sin 12)/( (√(1+((sin^2 66)/(cos^2 72))−((2 sin 66 cos 12)/(cos 72)))))) =6°
$${say}\:{AD}=\mathrm{1} \\ $$$${AB}={BD}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{72}} \\ $$$$\frac{{AD}}{\mathrm{sin}\:\mathrm{66}}=\frac{{CD}}{\mathrm{sin}\:\mathrm{30}} \\ $$$$\Rightarrow{CD}=\frac{{AD}\:\mathrm{sin}\:\mathrm{30}}{\mathrm{sin}\:\mathrm{66}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}} \\ $$$${BC}=\sqrt{{CD}^{\mathrm{2}} +{BD}^{\mathrm{2}} −\mathrm{2}×{CD}×{BD}×\mathrm{cos}\:\mathrm{12}} \\ $$$${BC}=\sqrt{\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{66}}+\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{72}}−\frac{\mathrm{cos}\:\mathrm{12}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}\:\mathrm{cos}\:\mathrm{72}}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{CD}}=\frac{\mathrm{sin}\:\mathrm{12}}{{BC}} \\ $$$$\mathrm{sin}\:\alpha=\frac{{CD}\:\mathrm{sin}\:\mathrm{12}}{{BC}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}\:\sqrt{\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{66}}+\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{72}}−\frac{\mathrm{cos}\:\mathrm{12}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}\:\mathrm{cos}\:\mathrm{72}}}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{12}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{66}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{72}}−\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}\:\mathrm{cos}\:\mathrm{12}}{\mathrm{cos}\:\mathrm{72}}}} \\ $$$$\alpha=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{sin}\:\mathrm{12}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{66}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{72}}−\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{66}\:\mathrm{cos}\:\mathrm{12}}{\mathrm{cos}\:\mathrm{72}}}} \\ $$$$=\mathrm{6}° \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
superb ! Thank you very much Sir.
$$\mathrm{superb}\:!\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *