Menu Close

Question-97007

Tinku Tara 0 Comments
Pin




Question Number 97007 by bagjamath last updated on 06/Jun/20
Commented by bagjamath last updated on 06/Jun/20
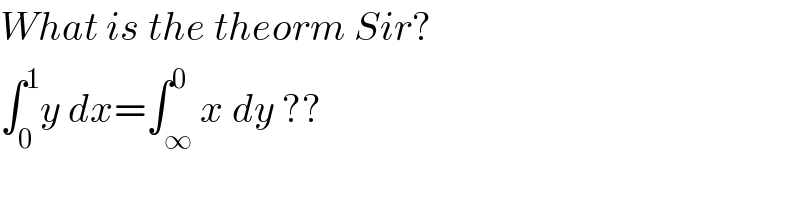
What is the theorm Sir? ∫_0 ^1 y dx=∫_∞ ^0 x dy ??
$${What}\:{is}\:{the}\:{theorm}\:{Sir}? \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {y}\:{dx}=\int_{\infty} ^{\mathrm{0}} {x}\:{dy}\:?? \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
Itdoes not make any sense.
$$\mathrm{Itdoes}\:\mathrm{not}\:\mathrm{make}\:\mathrm{any}\:\mathrm{sense}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
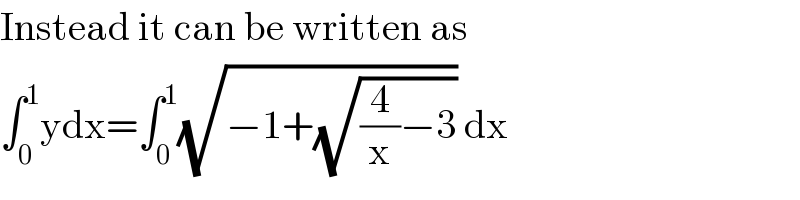
Instead it can be written as ∫_0 ^1 ydx=∫_0 ^1 (√(−1+(√((4/x)−3)))) dx
$$\mathrm{Instead}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ydx}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{−\mathrm{1}+\sqrt{\frac{\mathrm{4}}{\mathrm{x}}−\mathrm{3}}}\:\mathrm{dx} \\ $$
Commented by bagjamath last updated on 06/Jun/20
Commented by bagjamath last updated on 06/Jun/20
This is question
$${This}\:{is}\:{question} \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
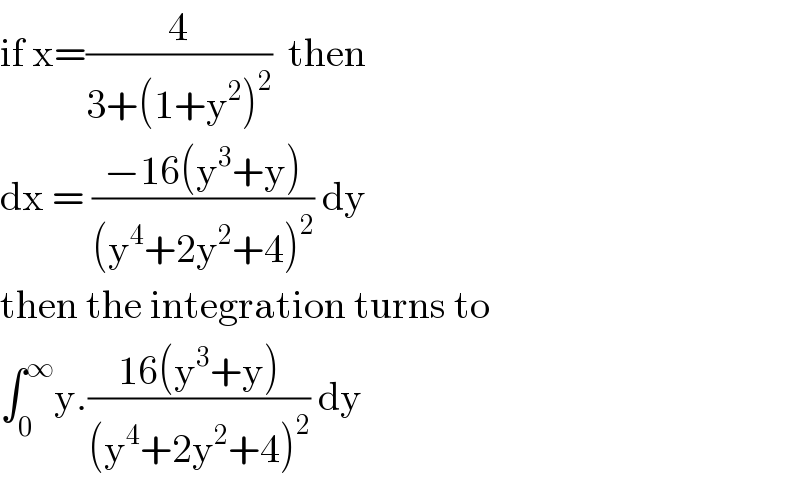
if x=(4/(3+(1+y^2 )^2 )) then dx = ((−16(y^3 +y))/((y^4 +2y^2 +4)^2 )) dy then the integration turns to ∫_0 ^∞ y.((16(y^3 +y))/((y^4 +2y^2 +4)^2 )) dy
$$\mathrm{if}\:\mathrm{x}=\frac{\mathrm{4}}{\mathrm{3}+\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\mathrm{then} \\ $$$$\mathrm{dx}\:=\:\frac{−\mathrm{16}\left(\mathrm{y}^{\mathrm{3}} +\mathrm{y}\right)}{\left(\mathrm{y}^{\mathrm{4}} +\mathrm{2y}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }\:\mathrm{dy} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{integration}\:\mathrm{turns}\:\mathrm{to} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{y}.\frac{\mathrm{16}\left(\mathrm{y}^{\mathrm{3}} +\mathrm{y}\right)}{\left(\mathrm{y}^{\mathrm{4}} +\mathrm{2y}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }\:\mathrm{dy} \\ $$
Commented by mr W last updated on 06/Jun/20
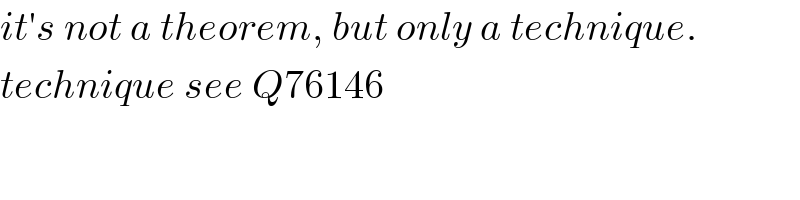
it′s not a theorem, but only a technique. technique see Q76146
$${it}'{s}\:{not}\:{a}\:{theorem},\:{but}\:{only}\:{a}\:{technique}. \\ $$$${technique}\:{see}\:{Q}\mathrm{76146} \\ $$
Commented by mr W last updated on 06/Jun/20
see also Q76680
$${see}\:{also}\:{Q}\mathrm{76680} \\ $$
Commented by mr W last updated on 06/Jun/20
Commented by mr W last updated on 06/Jun/20
the technique is following: ∫_0 ^1 ydx=∫_0 ^1 f(x)dx is the area under the curve (shaded area). this area can also be calculated as ∫_0 ^∞ xdy=∫_0 ^∞ f^(−1) (x)dx. in our case the calculation of ∫_0 ^∞ f^(−1) (x)dx is much easier than ∫_0 ^1 f(x)dx.
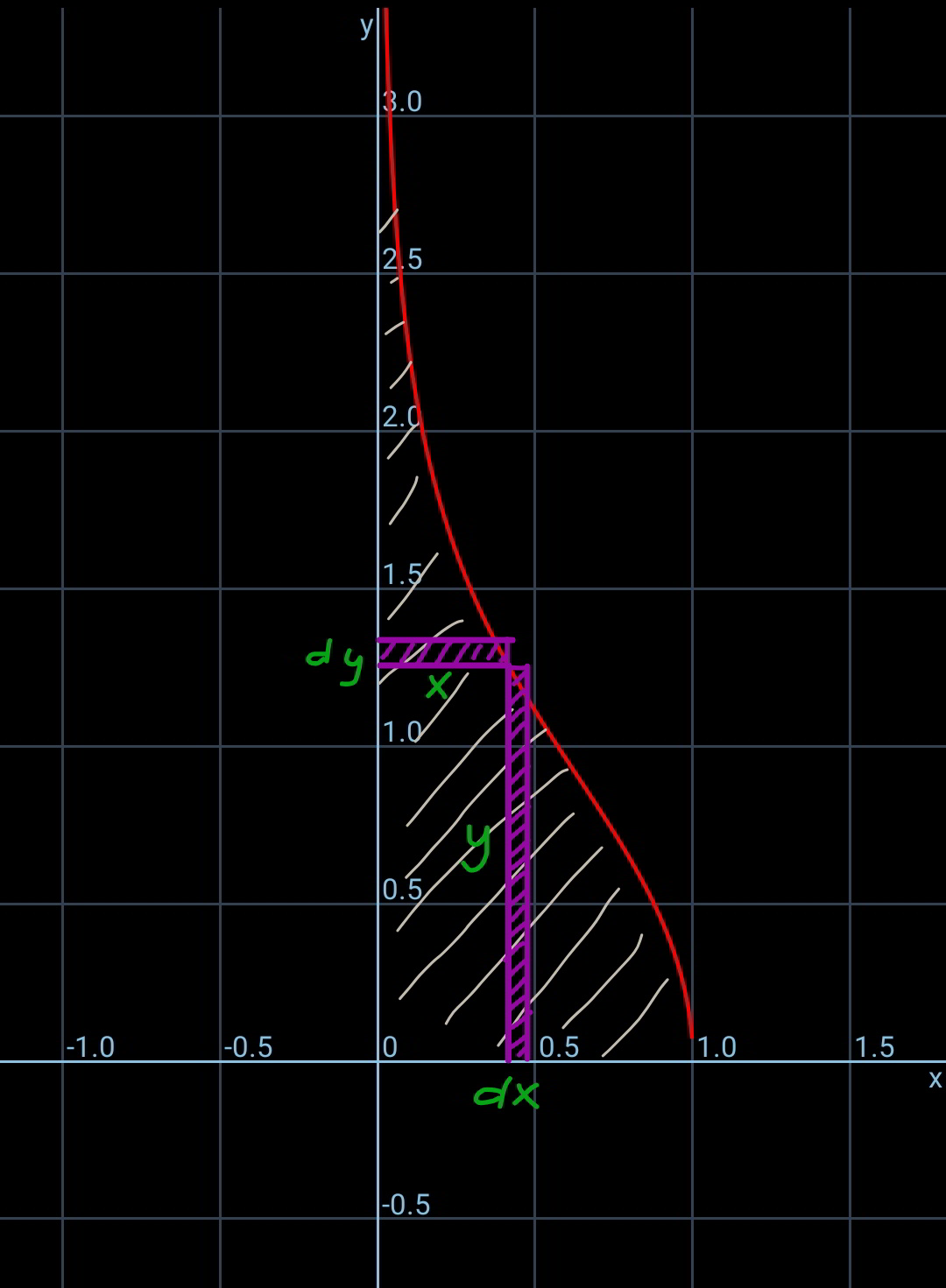
$${the}\:{technique}\:{is}\:{following}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ydx}=\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:{is}\:{the}\:{area}\:{under} \\ $$$${the}\:{curve}\:\left({shaded}\:{area}\right). \\ $$$${this}\:{area}\:{can}\:{also}\:{be}\:{calculated}\:{as} \\ $$$$\int_{\mathrm{0}} ^{\infty} {xdy}=\int_{\mathrm{0}} ^{\infty} {f}^{−\mathrm{1}} \left({x}\right){dx}. \\ $$$${in}\:{our}\:{case}\:{the}\:{calculation}\:{of} \\ $$$$\int_{\mathrm{0}} ^{\infty} {f}^{−\mathrm{1}} \left({x}\right){dx}\:{is}\:{much}\:{easier}\:{than} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
yes sir it is the concept of inverse function. Thank you. But I think in the question it should be mentioned somewhere as x is a function of y. Then this misunderstood can be avoided.
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\mathrm{concept}\:\mathrm{of}\:\mathrm{inverse}\:\mathrm{function}. \\ $$$$\mathrm{Thank}\:\mathrm{you}.\:\mathrm{But}\:\mathrm{I}\:\mathrm{think}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\:\mathrm{it}\:\mathrm{should} \\ $$$$\mathrm{be}\:\mathrm{mentioned}\:\mathrm{somewhere}\:\mathrm{as}\:\mathrm{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of} \\ $$$$\mathrm{y}.\:\mathrm{Then}\:\mathrm{this}\:\mathrm{misunderstood}\:\mathrm{can}\:\mathrm{be}\:\mathrm{avoided}. \\ $$
Commented by bagjamath last updated on 06/Jun/20
Thank You Sir, Now i understand
$${Thank}\:{You}\:{Sir},\:{Now}\:{i}\:{understand} \\ $$
Commented by bagjamath last updated on 06/Jun/20
What application do you use, Sir?
$${What}\:{application}\:{do}\:{you}\:{use},\:{Sir}? \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jun/20
you can use GeoGebra or Desmos
$$\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{GeoGebra}\:\mathrm{or}\:\mathrm{Desmos} \\ $$
Commented by abdomathmax last updated on 07/Jun/20
I =∫_0 ^1 (√(−1+(√((4/x)−3))))dx we do the changement (√(−1+(√((4/x)−3))))=t ⇒(√((4/x)−3))=t^2 +1 ⇒ (4/x) −3 =(t^2 +1)^(2 ) ⇒(4/x) =(t^(2 ) +1)^2 +3 ⇒ (x/4)=(1/((t^2 +1)^2 +3)) ⇒x =(4/((t^2 +1)^2 +3)) ⇒ dx =−4 ×((2(2t)(t^2 +1))/((t^2 +1)^(2 ) +3)) =−16 ×((t^3 +t)/((t^2 +1)^2 +3)) ⇒ I =16∫_0 ^∞ t× ((t^3 +t)/((t^2 +1)^2 +3))dt =16 ∫_0 ^∞ ((t^4 +t^2 )/((t^2 +1)^2 +3))dt =8 ∫_(−∞) ^(+∞) ((t^4 +t^2 )/((t^2 +1)^(2 ) +3))dt let ϕ(z) =((z^4 +z^2 )/((z^2 +1)^2 +3)) poles of ϕ? ϕ(z) =((z^4 +z^2 )/((z^2 +1−i(√3))(z^2 +1+i(√3)))) −1+i(√3)=2(−(1/2)+i((√3)/2)) =2e^((2iπ)/3) and− 1−i(√3)=2e^(−((2iπ)/3)) ϕ(z) =((z^4 +z^2 )/((z^2 −2e^((2iπ)/3) )(z^2 −2e^(−((i2π)/3)) ))) =((z^4 +z^2 )/((z−(√2)e^((iπ)/3) )(z+(√2)e^((iπ)/3) )(z−(√2)e^(−((iπ)/3)) )(z+(√2)e^(−((iπ)/3)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,(√2)e^((iπ)/3) )+Res(ϕ,−(√2)e^((−iπ)/3) )} Res(ϕ,(√2)e^((iπ)/3) ) =((4 e^((4iπ)/3) +2 e^((i2π)/3) )/(4(√2)e^((iπ)/3) (2i sin(((2π)/3))))) =((2 e^((4iπ)/3) +e^((i2π)/3) )/(4(√2)(i((√3)/2))))×e^(−((iπ)/3)) =((2 e^(iπ) +e^((iπ)/3) )/(2i(√2)(√3))) =((−2+e^((iπ)/3) )/(2i(√6))) Res(ϕ,−(√2)e^((−iπ)/3) ) = ((4 e^((−4iπ)/(3 )) +2 e^(−((2iπ)/3)) )/(−2(√2)e^(−((iπ)/3)) (2e^(−((2iπ)/3)) −2e^((2iπ)/3) ))) =((4 e^(−((4iπ)/3)) +2 e^(−((2iπ)/3)) )/(4(√2)(2isin(((2π)/3)))))×e^((iπ)/3) = ((2 e^(−iπ) +e^(−((iπ)/3)) )/(2(√3)(2i×((√3)/2)))) =((−2 +e^(−((iπ)/3)) )/(2i(√6))) ....be continued....
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{−\mathrm{1}+\sqrt{\frac{\mathrm{4}}{\mathrm{x}}−\mathrm{3}}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\sqrt{−\mathrm{1}+\sqrt{\frac{\mathrm{4}}{\mathrm{x}}−\mathrm{3}}}=\mathrm{t}\:\Rightarrow\sqrt{\frac{\mathrm{4}}{\mathrm{x}}−\mathrm{3}}=\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{4}}{\mathrm{x}}\:−\mathrm{3}\:=\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}\:} \:\Rightarrow\frac{\mathrm{4}}{\mathrm{x}}\:=\left(\mathrm{t}^{\mathrm{2}\:} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\:\Rightarrow \\ $$$$\frac{\mathrm{x}}{\mathrm{4}}=\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{4}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{dx}\:=−\mathrm{4}\:×\frac{\mathrm{2}\left(\mathrm{2t}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}\:} \:+\mathrm{3}}\:=−\mathrm{16}\:×\frac{\mathrm{t}^{\mathrm{3}} \:+\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{I}\:\:=\mathrm{16}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}×\:\frac{\mathrm{t}^{\mathrm{3}} \:+\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}}\mathrm{dt} \\ $$$$=\mathrm{16}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{4}} \:+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}}\mathrm{dt} \\ $$$$=\mathrm{8}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{4}} \:+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}\:} +\mathrm{3}}\mathrm{dt}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{4}} \:+\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}} \\ $$$$\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{4}} \:+\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\right)} \\ $$$$−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}=\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\mathrm{2e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:\mathrm{and}−\:\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}=\mathrm{2e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{4}} \:+\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} \:−\mathrm{2e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{2e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{\mathrm{z}^{\mathrm{4}} \:+\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}+\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}+\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi,\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)+\mathrm{Res}\left(\varphi,−\sqrt{\mathrm{2}}\mathrm{e}^{\frac{−\mathrm{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{4}\:\mathrm{e}^{\frac{\mathrm{4i}\pi}{\mathrm{3}}} \:+\mathrm{2}\:\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }{\mathrm{4}\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{2i}\:\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{\mathrm{2}\:\mathrm{e}^{\frac{\mathrm{4i}\pi}{\mathrm{3}}} +\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }{\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}×\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\:\:=\frac{\mathrm{2}\:\mathrm{e}^{\mathrm{i}\pi} \:+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\mathrm{2i}\sqrt{\mathrm{2}}\sqrt{\mathrm{3}}}\:=\frac{−\mathrm{2}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:}{\mathrm{2i}\sqrt{\mathrm{6}}} \\ $$$$\mathrm{Res}\left(\varphi,−\sqrt{\mathrm{2}}\mathrm{e}^{\frac{−\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\:\frac{\mathrm{4}\:\mathrm{e}^{\frac{−\mathrm{4i}\pi}{\mathrm{3}\:}} \:+\mathrm{2}\:\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{2e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} −\mathrm{2e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{\mathrm{4}\:\mathrm{e}^{−\frac{\mathrm{4i}\pi}{\mathrm{3}}} \:+\mathrm{2}\:\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}×\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:=\:\frac{\mathrm{2}\:\mathrm{e}^{−\mathrm{i}\pi} \:+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\mathrm{2}\sqrt{\mathrm{3}}\left(\mathrm{2i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \\ $$$$=\frac{−\mathrm{2}\:+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\mathrm{2i}\sqrt{\mathrm{6}}}\:\:….\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 07/Jun/20
error in dx i will delete the post!
$$\mathrm{error}\:\mathrm{in}\:\mathrm{dx}\:\:\mathrm{i}\:\mathrm{will}\:\mathrm{delete}\:\mathrm{the}\:\mathrm{post}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *