Question-97082

Facebook Tweet Pin

Question Number 97082 by bobhans last updated on 06/Jun/20

Answered by john santu last updated on 06/Jun/20

Commented by bobhans last updated on 06/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by mathmax by abdo last updated on 06/Jun/20

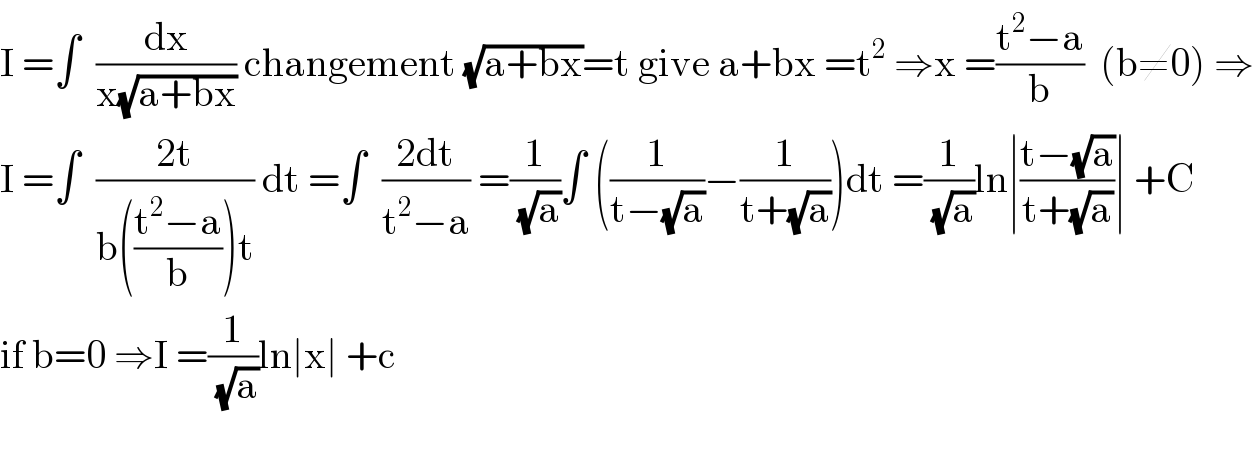
I =∫ (dx/(x(√(a+bx)))) changement (√(a+bx))=t give a+bx =t^2 ⇒x =((t^2 −a)/b) (b≠0) ⇒ I =∫ ((2t)/(b(((t^2 −a)/b))t)) dt =∫ ((2dt)/(t^2 −a)) =(1/( (√a)))∫ ((1/(t−(√a)))−(1/(t+(√a))))dt =(1/( (√a)))ln∣((t−(√a))/(t+(√a)))∣ +C if b=0 ⇒I =(1/( (√a)))ln∣x∣ +c

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{a}+\mathrm{bx}}}\:\mathrm{changement}\:\sqrt{\mathrm{a}+\mathrm{bx}}=\mathrm{t}\:\mathrm{give}\:\mathrm{a}+\mathrm{bx}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{a}}{\mathrm{b}}\:\:\left(\mathrm{b}\neq\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{2t}}{\mathrm{b}\left(\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{a}}{\mathrm{b}}\right)\mathrm{t}}\:\mathrm{dt}\:=\int\:\:\frac{\mathrm{2dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{a}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\int\:\left(\frac{\mathrm{1}}{\mathrm{t}−\sqrt{\mathrm{a}}}−\frac{\mathrm{1}}{\mathrm{t}+\sqrt{\mathrm{a}}}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\mathrm{ln}\mid\frac{\mathrm{t}−\sqrt{\mathrm{a}}}{\mathrm{t}+\sqrt{\mathrm{a}}}\mid\:+\mathrm{C} \\ $$$$\mathrm{if}\:\mathrm{b}=\mathrm{0}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\mathrm{ln}\mid\mathrm{x}\mid\:+\mathrm{c} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 06/Jun/20

t=(√(a+bx)) ⇒ I =(1/( (√a)))ln∣(((√(a+bx))−(√a))/( (√(a+bx))+(√a)))∣ +C

$$\mathrm{t}=\sqrt{\mathrm{a}+\mathrm{bx}}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{a}+\mathrm{bx}}−\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{a}+\mathrm{bx}}+\sqrt{\mathrm{a}}}\mid\:+\mathrm{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply