Menu Close

Question-97206

Tinku Tara 0 Comments
Pin




Question Number 97206 by O Predador last updated on 07/Jun/20
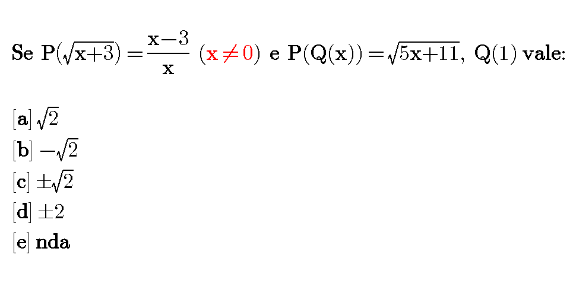
Answered by john santu last updated on 07/Jun/20
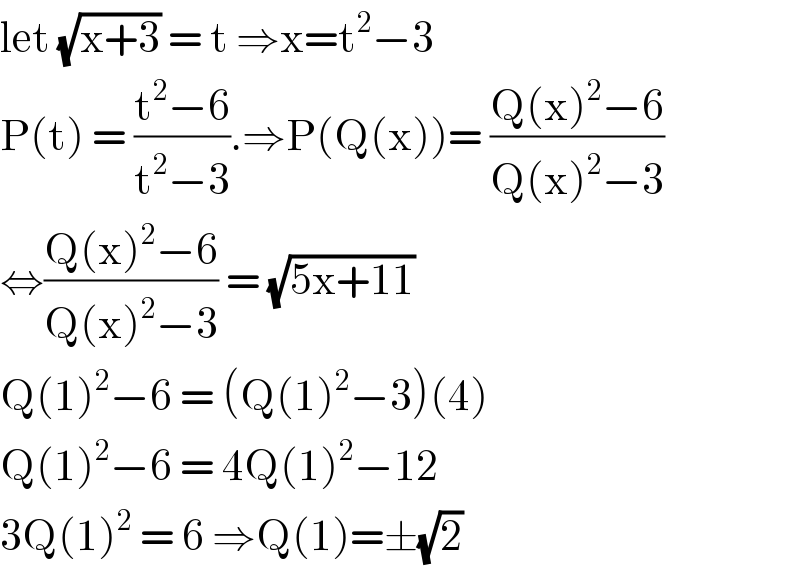
let (√(x+3)) = t ⇒x=t^2 −3 P(t) = ((t^2 −6)/(t^2 −3)).⇒P(Q(x))= ((Q(x)^2 −6)/(Q(x)^2 −3)) ⇔((Q(x)^2 −6)/(Q(x)^2 −3)) = (√(5x+11)) Q(1)^2 −6 = (Q(1)^2 −3)(4) Q(1)^2 −6 = 4Q(1)^2 −12 3Q(1)^2 = 6 ⇒Q(1)=±(√2)
$$\mathrm{let}\:\sqrt{\mathrm{x}+\mathrm{3}}\:=\:\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{P}\left(\mathrm{t}\right)\:=\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{6}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3}}.\Rightarrow\mathrm{P}\left(\mathrm{Q}\left(\mathrm{x}\right)\right)=\:\frac{\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} −\mathrm{6}}{\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} −\mathrm{3}} \\ $$$$\Leftrightarrow\frac{\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} −\mathrm{6}}{\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} −\mathrm{3}}\:=\:\sqrt{\mathrm{5x}+\mathrm{11}} \\ $$$$\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}\:=\:\left(\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{4}\right) \\ $$$$\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}\:=\:\mathrm{4Q}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{12} \\ $$$$\mathrm{3Q}\left(\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{6}\:\Rightarrow\mathrm{Q}\left(\mathrm{1}\right)=\pm\sqrt{\mathrm{2}} \\ $$
Commented by O Predador last updated on 07/Jun/20
Thank you!
$$\:\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}! \\ $$
Answered by mathmax by abdo last updated on 07/Jun/20
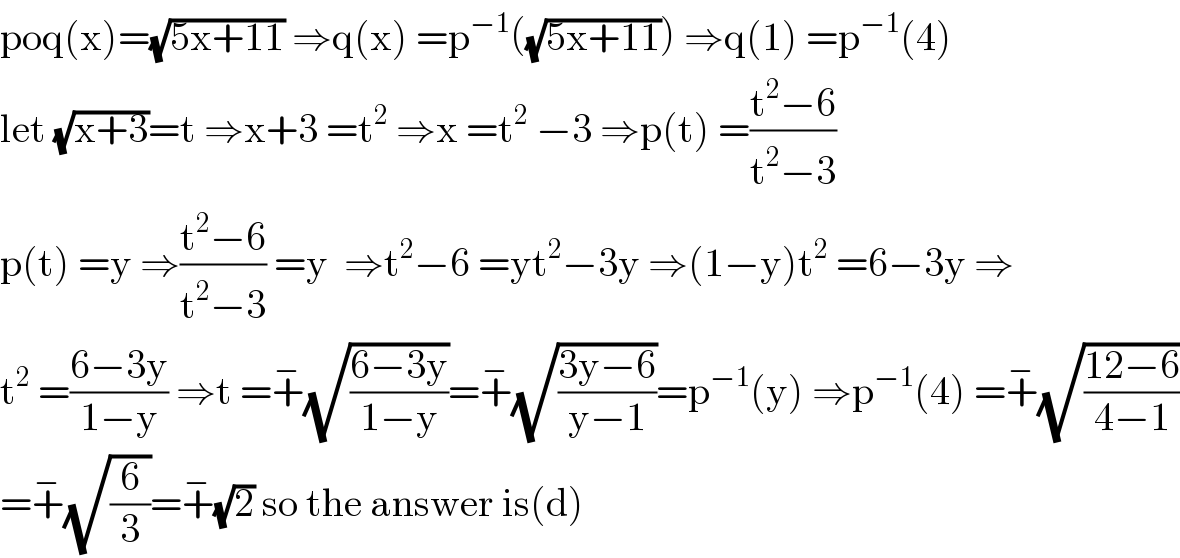
poq(x)=(√(5x+11)) ⇒q(x) =p^(−1) ((√(5x+11))) ⇒q(1) =p^(−1) (4) let (√(x+3))=t ⇒x+3 =t^2 ⇒x =t^2 −3 ⇒p(t) =((t^2 −6)/(t^2 −3)) p(t) =y ⇒((t^2 −6)/(t^2 −3)) =y ⇒t^2 −6 =yt^2 −3y ⇒(1−y)t^2 =6−3y ⇒ t^2 =((6−3y)/(1−y)) ⇒t =+^− (√((6−3y)/(1−y)))=+^− (√((3y−6)/(y−1)))=p^(−1) (y) ⇒p^(−1) (4) =+^− (√((12−6)/(4−1))) =+^− (√(6/3))=+^− (√2) so the answer is(d)
$$\mathrm{poq}\left(\mathrm{x}\right)=\sqrt{\mathrm{5x}+\mathrm{11}}\:\Rightarrow\mathrm{q}\left(\mathrm{x}\right)\:=\mathrm{p}^{−\mathrm{1}} \left(\sqrt{\mathrm{5x}+\mathrm{11}}\right)\:\Rightarrow\mathrm{q}\left(\mathrm{1}\right)\:=\mathrm{p}^{−\mathrm{1}} \left(\mathrm{4}\right) \\ $$$$\mathrm{let}\:\sqrt{\mathrm{x}+\mathrm{3}}=\mathrm{t}\:\Rightarrow\mathrm{x}+\mathrm{3}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} \:−\mathrm{3}\:\Rightarrow\mathrm{p}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{6}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3}} \\ $$$$\mathrm{p}\left(\mathrm{t}\right)\:=\mathrm{y}\:\Rightarrow\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{6}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3}}\:=\mathrm{y}\:\:\Rightarrow\mathrm{t}^{\mathrm{2}} −\mathrm{6}\:=\mathrm{yt}^{\mathrm{2}} −\mathrm{3y}\:\Rightarrow\left(\mathrm{1}−\mathrm{y}\right)\mathrm{t}^{\mathrm{2}} \:=\mathrm{6}−\mathrm{3y}\:\Rightarrow \\ $$$$\mathrm{t}^{\mathrm{2}} \:=\frac{\mathrm{6}−\mathrm{3y}}{\mathrm{1}−\mathrm{y}}\:\Rightarrow\mathrm{t}\:=\overset{−} {+}\sqrt{\frac{\mathrm{6}−\mathrm{3y}}{\mathrm{1}−\mathrm{y}}}=\overset{−} {+}\sqrt{\frac{\mathrm{3y}−\mathrm{6}}{\mathrm{y}−\mathrm{1}}}=\mathrm{p}^{−\mathrm{1}} \left(\mathrm{y}\right)\:\Rightarrow\mathrm{p}^{−\mathrm{1}} \left(\mathrm{4}\right)\:=\overset{−} {+}\sqrt{\frac{\mathrm{12}−\mathrm{6}}{\mathrm{4}−\mathrm{1}}} \\ $$$$=\overset{−} {+}\sqrt{\frac{\mathrm{6}}{\mathrm{3}}}=\overset{−} {+}\sqrt{\mathrm{2}}\:\mathrm{so}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\left(\mathrm{d}\right) \\ $$
Commented by bobhans last updated on 07/Jun/20
typo. C
$$\mathrm{typo}.\:\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 07/Jun/20
yes .
$$\mathrm{yes}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *