Question Number 97227 by bemath last updated on 07/Jun/20
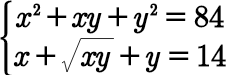
Commented by bemath last updated on 07/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\: \\ $$
Answered by som(math1967) last updated on 07/Jun/20
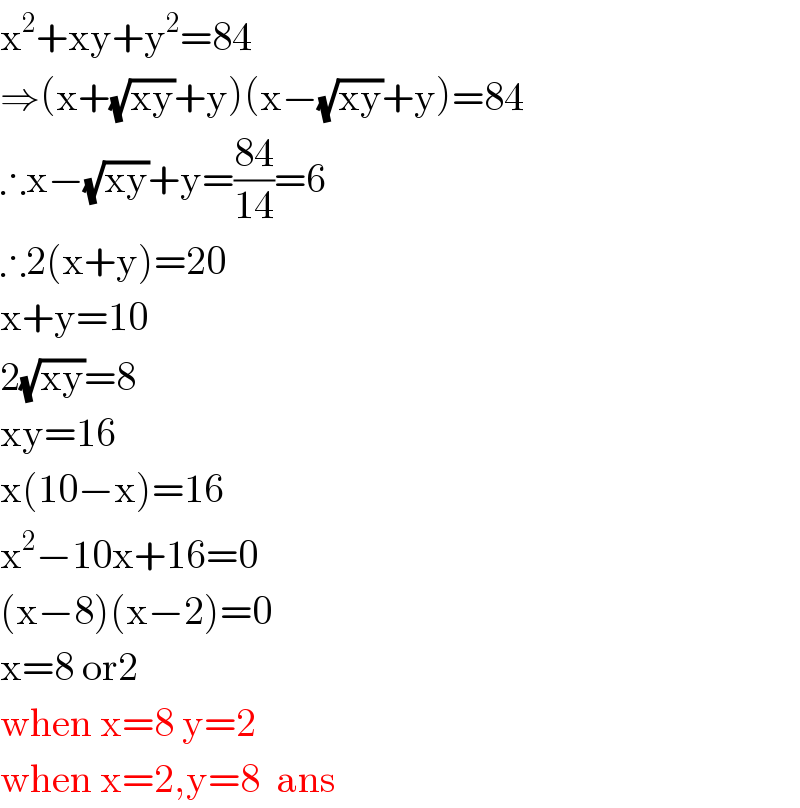
$$\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{84} \\ $$$$\Rightarrow\left(\mathrm{x}+\sqrt{\mathrm{xy}}+\mathrm{y}\right)\left(\mathrm{x}−\sqrt{\mathrm{xy}}+\mathrm{y}\right)=\mathrm{84} \\ $$$$\therefore\mathrm{x}−\sqrt{\mathrm{xy}}+\mathrm{y}=\frac{\mathrm{84}}{\mathrm{14}}=\mathrm{6} \\ $$$$\therefore\mathrm{2}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{20} \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{10} \\ $$$$\mathrm{2}\sqrt{\mathrm{xy}}=\mathrm{8} \\ $$$$\mathrm{xy}=\mathrm{16} \\ $$$$\mathrm{x}\left(\mathrm{10}−\mathrm{x}\right)=\mathrm{16} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{16}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{8}\right)\left(\mathrm{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{8}\:\mathrm{or2} \\ $$$$\mathrm{when}\:\mathrm{x}=\mathrm{8}\:\mathrm{y}=\mathrm{2} \\ $$$$\mathrm{when}\:\mathrm{x}=\mathrm{2},\mathrm{y}=\mathrm{8}\:\:\mathrm{ans} \\ $$
Answered by john santu last updated on 07/Jun/20

$$\Leftrightarrow{x}^{\mathrm{2}} +\mathrm{2}{xy}+{y}^{\mathrm{2}} −{xy}\:=\:\mathrm{84}\: \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\left(\sqrt{{xy}}\right)^{\mathrm{2}} \:=\:\mathrm{84}\: \\ $$$$\left({x}+{y}+\sqrt{{xy}}\right)\left({x}+{y}−\sqrt{{xy}}\right)\:=\:\mathrm{84} \\ $$$$\Leftrightarrow\mathrm{14}\:×\left({x}+{y}−\sqrt{{xy}}\right)\:=\:\mathrm{84} \\ $$$${x}+{y}−\sqrt{{xy}}\:=\:\mathrm{6}\:…\left(\mathrm{2}\right) \\ $$$${x}+{y}+\sqrt{{xy}}\:=\:\mathrm{14}\:…\left(\mathrm{1}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\:+\: \\ $$$${x}+{y}\:=\:\mathrm{10}\:\wedge\:\sqrt{{xy}}\:=\:\mathrm{4}\: \\ $$$$\Leftrightarrow\:{x}\left(\mathrm{10}−{x}\right)\:=\:\mathrm{16}\: \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{16}\:=\:\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}−\mathrm{8}\right)\:=\:\mathrm{0}\: \\ $$$$\begin{cases}{{x}=\mathrm{2}\:\wedge\mathrm{y}=\mathrm{8}}\\{{x}=\mathrm{8}\:\wedge\mathrm{y}=\mathrm{2}}\end{cases} \\ $$
