Menu Close

Question-97236

Tinku Tara 0 Comments
Pin




Question Number 97236 by bemath last updated on 07/Jun/20
Commented by mr W last updated on 07/Jun/20
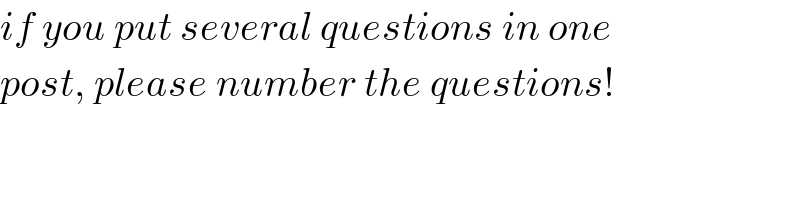
if you put several questions in one post, please number the questions!
$${if}\:{you}\:{put}\:{several}\:{questions}\:{in}\:{one} \\ $$$${post},\:{please}\:{number}\:{the}\:{questions}! \\ $$
Commented by bemath last updated on 07/Jun/20
hahaha...sorry sir
$$\mathrm{hahaha}…\mathrm{sorry}\:\mathrm{sir} \\ $$
Commented by bemath last updated on 07/Jun/20
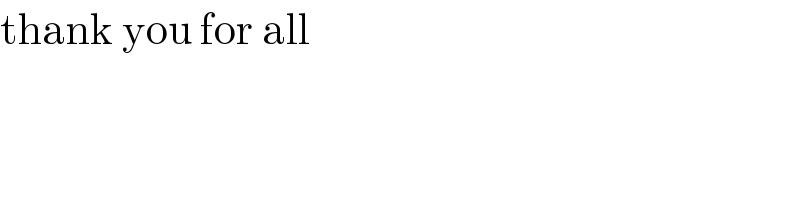
thank you for all
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{all} \\ $$
Answered by john santu last updated on 07/Jun/20
Commented by mahdi last updated on 07/Jun/20
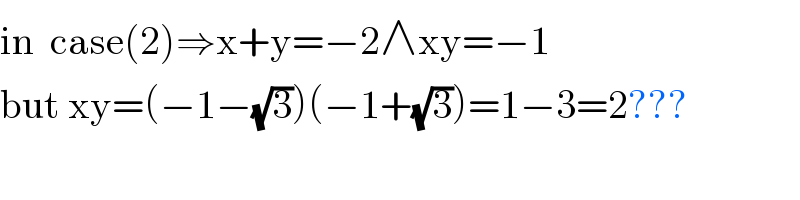
in case(2)⇒x+y=−2∧xy=−1 but xy=(−1−(√3))(−1+(√3))=1−3=2???
$$\mathrm{in}\:\:\mathrm{case}\left(\mathrm{2}\right)\Rightarrow\mathrm{x}+\mathrm{y}=−\mathrm{2}\wedge\mathrm{xy}=−\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{xy}=\left(−\mathrm{1}−\sqrt{\mathrm{3}}\right)\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right)=\mathrm{1}−\mathrm{3}=\mathrm{2}??? \\ $$
Answered by mahdi last updated on 19/Jun/20
1− { ((x^2 −xy+y^2 =7)),((x−xy+y=−1)) :}⇒^+ x^2 −2xy+y^2 +x+y=6 ⇒(x−y)^2 +(x+y)=6 [I] { ((x^2 −xy+y^2 =7)),((−3x+3xy−3y=3)) :}⇒^+ x^2 +2xy+y^2 −3(x+y)=10 ⇒(x+y)^2 −3(x+y)=10 [II] ⇒^(II) { (((x+y)=5⇒^I { (((x−y)=1 ⇒x=3,y=2)),(((x−y)=−1⇒x=2,y=3)) :})),(((x+y)=−2⇒^I { (((x−y)=2(√2)⇒x=(√2)−1,y=−(√2)−1)),(((x−y)=−2(√2)⇒x=−(√2)−1,y=(√2)−1)) :})) :} {(2,3),(3,2),((√2)−1,−(√2)−1),(−(√2)−1,(√2)−1)}⇒ans1 2− { (( D_f f(x) R_f )),((x<1 9−3x (6,+∞))),((1≤x≤3 7−x [4,6])),((3<x<5 x+1 (4,6) )),((5≤x 3x−9 [6,+∞))) :} min=4 3−((log((a/b)))/(log(b)))=((log(a)−log(b))/(log(b)))=((log(a))/(log(b)))−1 =1000−1=999 4−((3+x)/(4+x))=((6+x)/(8+x))⇒(3+x)(8+x)=(6+x)(4+x)⇒ x^2 +11x+24=x^2 +10x+24⇒x=0 5−S=((p(p−a)(p−b)(p−c)))^(1/�) (p=((a+b+c)/2)) (heron′L) S≈90
$$\mathrm{1}−\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{7}}\\{\mathrm{x}−\mathrm{xy}+\mathrm{y}=−\mathrm{1}}\end{cases}\overset{+} {\Rightarrow}\mathrm{x}^{\mathrm{2}} −\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} +\mathrm{x}+\mathrm{y}=\mathrm{6} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{6}\:\:\left[\mathrm{I}\right] \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{7}}\\{−\mathrm{3x}+\mathrm{3xy}−\mathrm{3y}=\mathrm{3}}\end{cases}\overset{+} {\Rightarrow}\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{10} \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{10}\:\:\:\:\left[\mathrm{II}\right] \\ $$$$\overset{\mathrm{II}} {\Rightarrow}\begin{cases}{\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{5}\overset{\mathrm{I}} {\Rightarrow}\begin{cases}{\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{1}\:\Rightarrow\mathrm{x}=\mathrm{3},\mathrm{y}=\mathrm{2}}\\{\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{2},\mathrm{y}=\mathrm{3}}\end{cases}}\\{\left(\mathrm{x}+\mathrm{y}\right)=−\mathrm{2}\overset{\mathrm{I}} {\Rightarrow}\begin{cases}{\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{2}\sqrt{\mathrm{2}}\Rightarrow\mathrm{x}=\sqrt{\mathrm{2}}−\mathrm{1},\mathrm{y}=−\sqrt{\mathrm{2}}−\mathrm{1}}\\{\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{2}\sqrt{\mathrm{2}}\Rightarrow\mathrm{x}=−\sqrt{\mathrm{2}}−\mathrm{1},\mathrm{y}=\sqrt{\mathrm{2}}−\mathrm{1}}\end{cases}}\end{cases} \\ $$$$\left\{\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{3},\mathrm{2}\right),\left(\sqrt{\mathrm{2}}−\mathrm{1},−\sqrt{\mathrm{2}}−\mathrm{1}\right),\left(−\sqrt{\mathrm{2}}−\mathrm{1},\sqrt{\mathrm{2}}−\mathrm{1}\right)\right\}\Rightarrow\mathrm{ans1} \\ $$$$\mathrm{2}−\begin{cases}{\:\:\mathrm{D}_{\mathrm{f}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\mathrm{R}_{\mathrm{f}} \:}\\{\mathrm{x}<\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}−\mathrm{3x}\:\:\:\:\:\left(\mathrm{6},+\infty\right)}\\{\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{3}\:\:\:\:\:\:\mathrm{7}−\mathrm{x}\:\:\:\:\:\:\:\:\left[\mathrm{4},\mathrm{6}\right]}\\{\mathrm{3}<\mathrm{x}<\mathrm{5}\:\:\:\:\:\:\mathrm{x}+\mathrm{1}\:\:\:\:\:\:\:\:\left(\mathrm{4},\mathrm{6}\right)\:}\\{\mathrm{5}\leqslant\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}−\mathrm{9}\:\:\:\:\:\:\left[\mathrm{6},+\infty\right)}\end{cases} \\ $$$$\mathrm{min}=\mathrm{4} \\ $$$$\mathrm{3}−\frac{\mathrm{log}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)}{\mathrm{log}\left(\mathrm{b}\right)}=\frac{\mathrm{log}\left(\mathrm{a}\right)−\mathrm{log}\left(\mathrm{b}\right)}{\mathrm{log}\left(\mathrm{b}\right)}=\frac{\mathrm{log}\left(\mathrm{a}\right)}{\mathrm{log}\left(\mathrm{b}\right)}−\mathrm{1} \\ $$$$=\mathrm{1000}−\mathrm{1}=\mathrm{999} \\ $$$$\mathrm{4}−\frac{\mathrm{3}+\mathrm{x}}{\mathrm{4}+\mathrm{x}}=\frac{\mathrm{6}+\mathrm{x}}{\mathrm{8}+\mathrm{x}}\Rightarrow\left(\mathrm{3}+\mathrm{x}\right)\left(\mathrm{8}+\mathrm{x}\right)=\left(\mathrm{6}+\mathrm{x}\right)\left(\mathrm{4}+\mathrm{x}\right)\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{24}=\mathrm{x}^{\mathrm{2}} +\mathrm{10x}+\mathrm{24}\Rightarrow\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{5}−\mathrm{S}=\sqrt[{}]{\mathrm{p}\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{b}\right)\left(\mathrm{p}−\mathrm{c}\right)}\:\:\:\left(\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}}\right)\:\:\left(\mathrm{heron}'\mathrm{L}\right) \\ $$$$\mathrm{S}\approx\mathrm{90} \\ $$
Commented by bemath last updated on 08/Jun/20
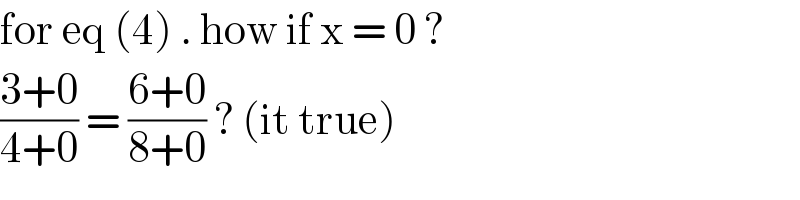
for eq (4) . how if x = 0 ? ((3+0)/(4+0)) = ((6+0)/(8+0)) ? (it true)
$$\mathrm{for}\:\mathrm{eq}\:\left(\mathrm{4}\right)\:.\:\mathrm{how}\:\mathrm{if}\:\mathrm{x}\:=\:\mathrm{0}\:? \\ $$$$\frac{\mathrm{3}+\mathrm{0}}{\mathrm{4}+\mathrm{0}}\:=\:\frac{\mathrm{6}+\mathrm{0}}{\mathrm{8}+\mathrm{0}}\:?\:\left(\mathrm{it}\:\mathrm{true}\right) \\ $$
Commented by bemath last updated on 08/Jun/20
if x = −((14)/3) ⇔((3+(−((14)/3)))/(4+(−((14)/3)))) = ((9−14)/(12−14)) =((−5)/(−2)) = (5/2) ⇔((6+(−((14)/3)))/(8+(−((14)/3)))) = ((18−14)/(24−14)) = (4/(10)) = (2/5) clear (5/2) ≠ (2/5) . so x = −((14)/3) not solution
$$\mathrm{if}\:\mathrm{x}\:=\:−\frac{\mathrm{14}}{\mathrm{3}}\:\Leftrightarrow\frac{\mathrm{3}+\left(−\frac{\mathrm{14}}{\mathrm{3}}\right)}{\mathrm{4}+\left(−\frac{\mathrm{14}}{\mathrm{3}}\right)}\:=\:\frac{\mathrm{9}−\mathrm{14}}{\mathrm{12}−\mathrm{14}} \\ $$$$=\frac{−\mathrm{5}}{−\mathrm{2}}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\mathrm{6}+\left(−\frac{\mathrm{14}}{\mathrm{3}}\right)}{\mathrm{8}+\left(−\frac{\mathrm{14}}{\mathrm{3}}\right)}\:=\:\frac{\mathrm{18}−\mathrm{14}}{\mathrm{24}−\mathrm{14}}\:=\:\frac{\mathrm{4}}{\mathrm{10}}\:=\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{clear}\:\:\frac{\mathrm{5}}{\mathrm{2}}\:\neq\:\frac{\mathrm{2}}{\mathrm{5}}\:. \\ $$$$\mathrm{so}\:\mathrm{x}\:=\:−\frac{\mathrm{14}}{\mathrm{3}}\:\mathrm{not}\:\mathrm{solution}\: \\ $$
Commented by bemath last updated on 08/Jun/20
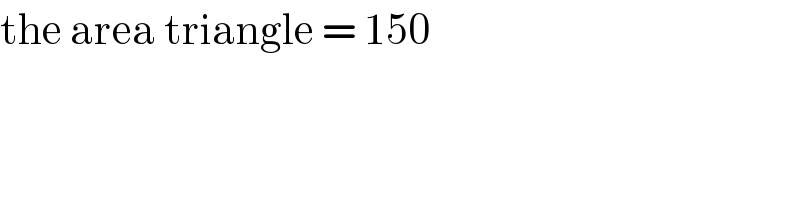
the area triangle = 150
$$\mathrm{the}\:\mathrm{area}\:\mathrm{triangle}\:=\:\mathrm{150} \\ $$
Commented by mahdi last updated on 19/Jun/20
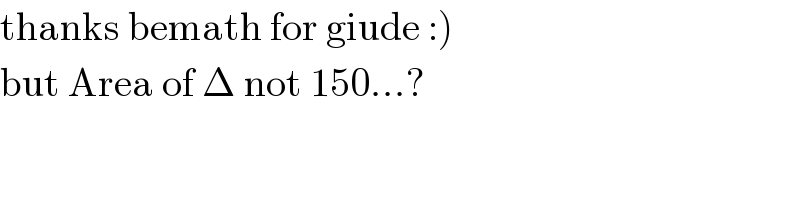
thanks bemath for giude :) but Area of Δ not 150...?
$$\left.\mathrm{thanks}\:\mathrm{bemath}\:\mathrm{for}\:\mathrm{giude}\::\right) \\ $$$$\mathrm{but}\:\mathrm{Area}\:\mathrm{of}\:\Delta\:\mathrm{not}\:\mathrm{150}…? \\ $$
Answered by mr W last updated on 07/Jun/20
Commented by PRITHWISH SEN 2 last updated on 07/Jun/20
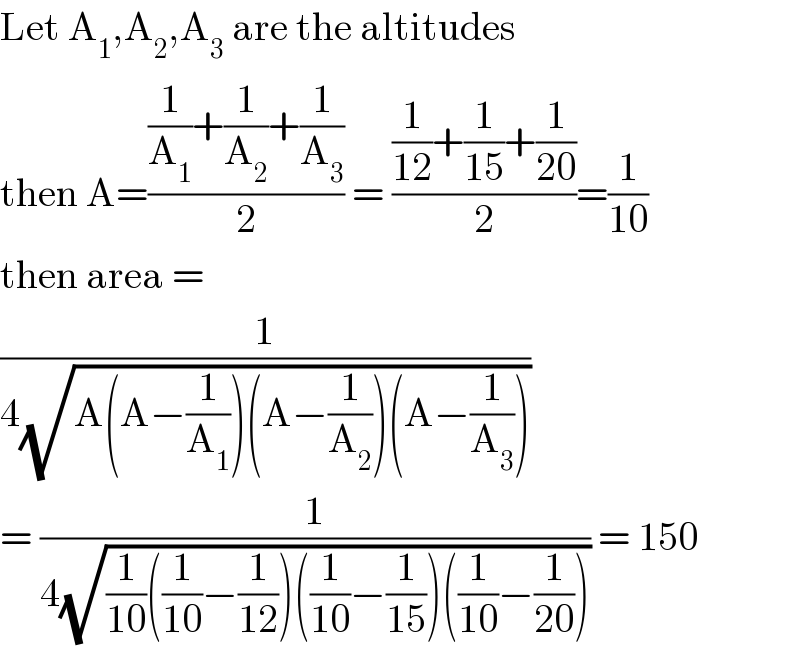
Let A_1 ,A_2 ,A_3 are the altitudes then A=(((1/A_1 )+(1/A_2 )+(1/A_3 ))/2) = (((1/(12))+(1/(15))+(1/(20)))/2)=(1/(10)) then area = (1/(4(√(A(A−(1/A_1 ))(A−(1/A_2 ))(A−(1/A_3 )))))) = (1/(4(√((1/(10))((1/(10))−(1/(12)))((1/(10))−(1/(15)))((1/(10))−(1/(20))))))) = 150
$$\mathrm{Let}\:\mathrm{A}_{\mathrm{1}} ,\mathrm{A}_{\mathrm{2}} ,\mathrm{A}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{altitudes} \\ $$$$\mathrm{then}\:\mathrm{A}=\frac{\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{3}} }}{\mathrm{2}}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{20}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\mathrm{then}\:\mathrm{area}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{A}\left(\mathrm{A}−\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{1}} }\right)\left(\mathrm{A}−\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{2}} }\right)\left(\mathrm{A}−\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{3}} }\right)}}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\frac{\mathrm{1}}{\mathrm{10}}\left(\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{12}}\right)\left(\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{15}}\right)\left(\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{20}}\right)}}\:=\:\mathrm{150} \\ $$
Commented by mr W last updated on 07/Jun/20
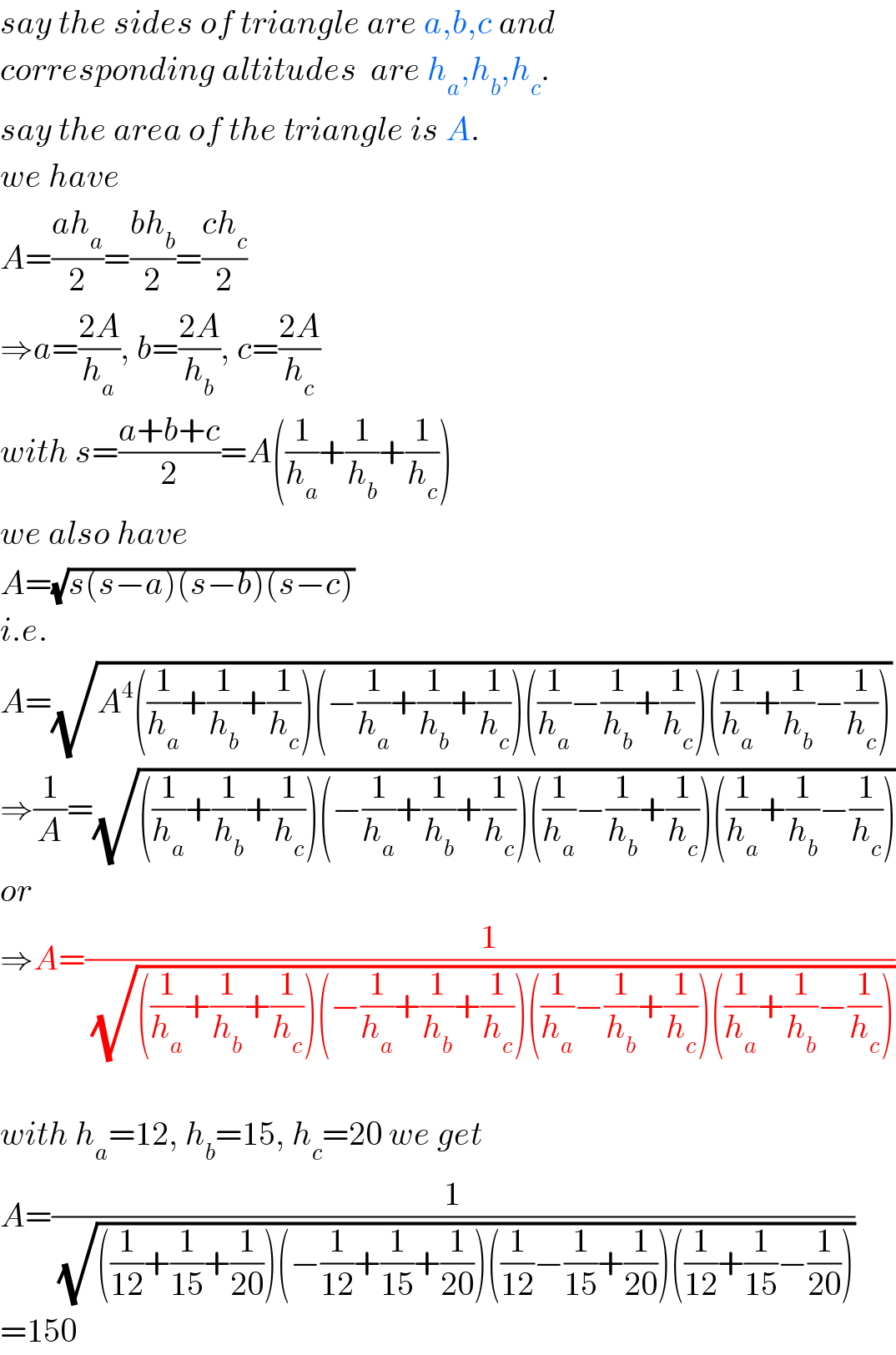
say the sides of triangle are a,b,c and corresponding altitudes are h_a ,h_b ,h_c . say the area of the triangle is A. we have A=((ah_a )/2)=((bh_b )/2)=((ch_c )/2) ⇒a=((2A)/h_a ), b=((2A)/h_b ), c=((2A)/h_c ) with s=((a+b+c)/2)=A((1/h_a )+(1/h_b )+(1/h_c )) we also have A=(√(s(s−a)(s−b)(s−c))) i.e. A=(√(A^4 ((1/h_a )+(1/h_b )+(1/h_c ))(−(1/h_a )+(1/h_b )+(1/h_c ))((1/h_a )−(1/h_b )+(1/h_c ))((1/h_a )+(1/h_b )−(1/h_c )))) ⇒(1/A)=(√(((1/h_a )+(1/h_b )+(1/h_c ))(−(1/h_a )+(1/h_b )+(1/h_c ))((1/h_a )−(1/h_b )+(1/h_c ))((1/h_a )+(1/h_b )−(1/h_c )))) or ⇒A=(1/( (√(((1/h_a )+(1/h_b )+(1/h_c ))(−(1/h_a )+(1/h_b )+(1/h_c ))((1/h_a )−(1/h_b )+(1/h_c ))((1/h_a )+(1/h_b )−(1/h_c )))))) with h_a =12, h_b =15, h_c =20 we get A=(1/( (√(((1/(12))+(1/(15))+(1/(20)))(−(1/(12))+(1/(15))+(1/(20)))((1/(12))−(1/(15))+(1/(20)))((1/(12))+(1/(15))−(1/(20))))))) =150
$${say}\:{the}\:{sides}\:{of}\:{triangle}\:{are}\:{a},{b},{c}\:{and} \\ $$$${corresponding}\:{altitudes}\:\:{are}\:{h}_{{a}} ,{h}_{{b}} ,{h}_{{c}} . \\ $$$${say}\:{the}\:{area}\:{of}\:{the}\:{triangle}\:{is}\:{A}. \\ $$$${we}\:{have} \\ $$$${A}=\frac{{ah}_{{a}} }{\mathrm{2}}=\frac{{bh}_{{b}} }{\mathrm{2}}=\frac{{ch}_{{c}} }{\mathrm{2}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2}{A}}{{h}_{{a}} },\:{b}=\frac{\mathrm{2}{A}}{{h}_{{b}} },\:{c}=\frac{\mathrm{2}{A}}{{h}_{{c}} } \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}}={A}\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right) \\ $$$${we}\:{also}\:{have} \\ $$$${A}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${i}.{e}. \\ $$$${A}=\sqrt{{A}^{\mathrm{4}} \left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(−\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }−\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }−\frac{\mathrm{1}}{{h}_{{c}} }\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{A}}=\sqrt{\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(−\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }−\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }−\frac{\mathrm{1}}{{h}_{{c}} }\right)} \\ $$$${or} \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\:\sqrt{\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(−\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }−\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }\right)\left(\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }−\frac{\mathrm{1}}{{h}_{{c}} }\right)}} \\ $$$$ \\ $$$${with}\:{h}_{{a}} =\mathrm{12},\:{h}_{{b}} =\mathrm{15},\:{h}_{{c}} =\mathrm{20}\:{we}\:{get} \\ $$$${A}=\frac{\mathrm{1}}{\:\sqrt{\left(\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{20}}\right)\left(−\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{15}}−\frac{\mathrm{1}}{\mathrm{20}}\right)}} \\ $$$$=\mathrm{150} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *