Question Number 97346 by bobhans last updated on 07/Jun/20

Answered by john santu last updated on 07/Jun/20
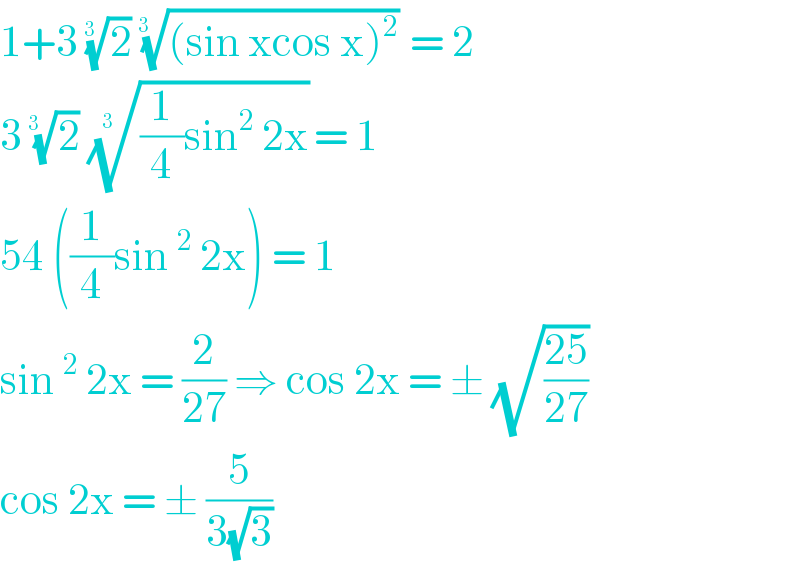
$$\mathrm{1}+\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{\mathrm{2}}\:\sqrt[{\mathrm{3}\:\:}]{\left(\mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$$\mathrm{3}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}}\:\sqrt[{\mathrm{3}\:\:}]{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \:\mathrm{2x}}=\:\mathrm{1} \\ $$$$\mathrm{54}\:\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2x}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2x}\:=\:\frac{\mathrm{2}}{\mathrm{27}}\:\Rightarrow\:\mathrm{cos}\:\mathrm{2x}\:=\:\pm\:\sqrt{\frac{\mathrm{25}}{\mathrm{27}}} \\ $$$$\mathrm{cos}\:\mathrm{2x}\:=\:\pm\:\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\: \\ $$
Commented by bobhans last updated on 08/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
