Menu Close

Question-97353

Tinku Tara 0 Comments
Pin




Question Number 97353 by john santu last updated on 07/Jun/20
Answered by abdomathmax last updated on 07/Jun/20
6) let f(x) =arcsin(((x−1)/(x+1))) and g(x)=2arctan(√x)−(π/2) f^′ (x) =(((((x−1)/(x+1)))^′ )/( (√(1−(((x−1)/(x+1)))^2 )))) =(2/((x+1)^2 (√(((x+1)^2 −(x−1)^2 )/((x+1)^2 ))))) =(2/((x+1)(√(x^2 +2x+1−x^2 +2x−1)))) =(2/((x+1)2(√x))) =(1/((x+1)(√x))) g^′ (x) =2 ((1/(2(√x)))/( (√(1+x)))) =(1/( (√x)(x+1))) ⇒ f(x)=g(x)+C C =f(0)−g(0) =−(π/2)−(−(π/2))=0 ⇒ f(x) =g(x) (with x≥0)
$$\left.\mathrm{6}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arcsin}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\:\mathrm{and}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{2arctan}\sqrt{\mathrm{x}}−\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\frac{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{'} }{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} }}\:=\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}−\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}}}\:=\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{2}\sqrt{\mathrm{x}}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}}} \\ $$$$\mathrm{g}^{'} \left(\mathrm{x}\right)\:=\mathrm{2}\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\:\sqrt{\mathrm{1}+\mathrm{x}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}\left(\mathrm{x}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{x}\right)+\mathrm{C} \\ $$$$\mathrm{C}\:=\mathrm{f}\left(\mathrm{0}\right)−\mathrm{g}\left(\mathrm{0}\right)\:=−\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{g}\left(\mathrm{x}\right)\:\:\left(\mathrm{with}\:\mathrm{x}\geqslant\mathrm{0}\right) \\ $$
Commented by john santu last updated on 08/Jun/20
thank you
$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Answered by abdomathmax last updated on 07/Jun/20
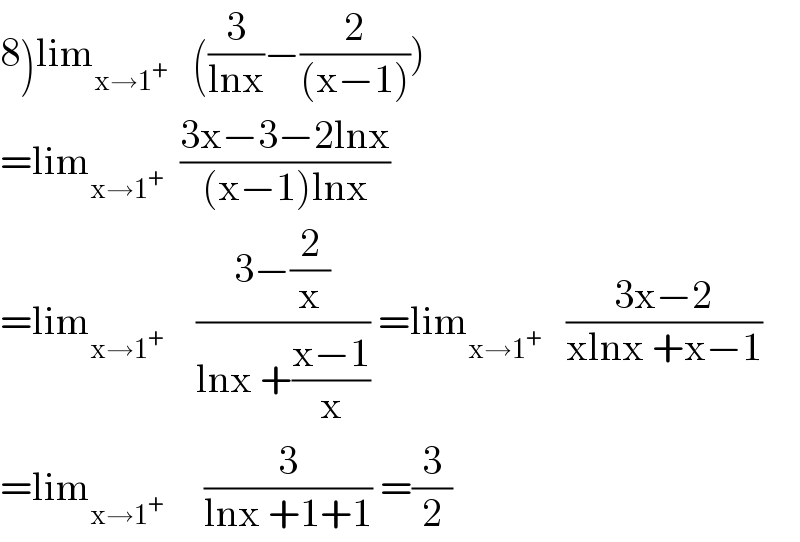
8)lim_(x→1^+ ) ((3/(lnx))−(2/((x−1)))) =lim_(x→1^+ ) ((3x−3−2lnx)/((x−1)lnx)) =lim_(x→1^+ ) ((3−(2/x))/(lnx +((x−1)/x))) =lim_(x→1^+ ) ((3x−2)/(xlnx +x−1)) =lim_(x→1^+ ) (3/(lnx +1+1)) =(3/2)
$$\left.\mathrm{8}\right)\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\left(\frac{\mathrm{3}}{\mathrm{lnx}}−\frac{\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)}\right) \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\frac{\mathrm{3x}−\mathrm{3}−\mathrm{2lnx}}{\left(\mathrm{x}−\mathrm{1}\right)\mathrm{lnx}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\:\frac{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{x}}}{\mathrm{lnx}\:+\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\frac{\mathrm{3x}−\mathrm{2}}{\mathrm{xlnx}\:+\mathrm{x}−\mathrm{1}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\:\:\frac{\mathrm{3}}{\mathrm{lnx}\:+\mathrm{1}+\mathrm{1}}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by abdomathmax last updated on 07/Jun/20
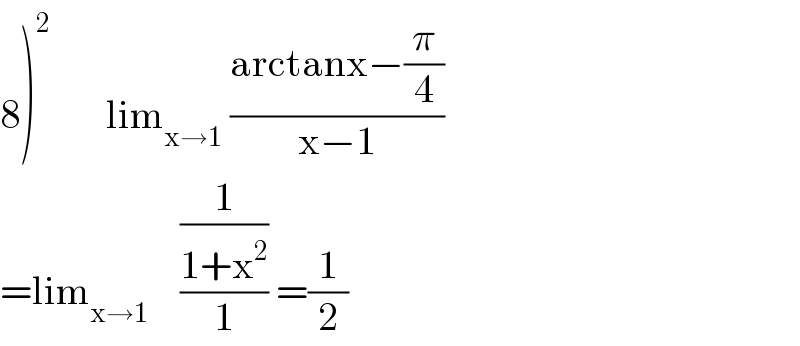
8)^2 lim_(x→1) ((arctanx−(π/4))/(x−1)) =lim_(x→1) ((1/(1+x^2 ))/1) =(1/2)
$$\left.\mathrm{8}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\frac{\mathrm{arctanx}−\frac{\pi}{\mathrm{4}}}{\mathrm{x}−\mathrm{1}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by abdomathmax last updated on 07/Jun/20
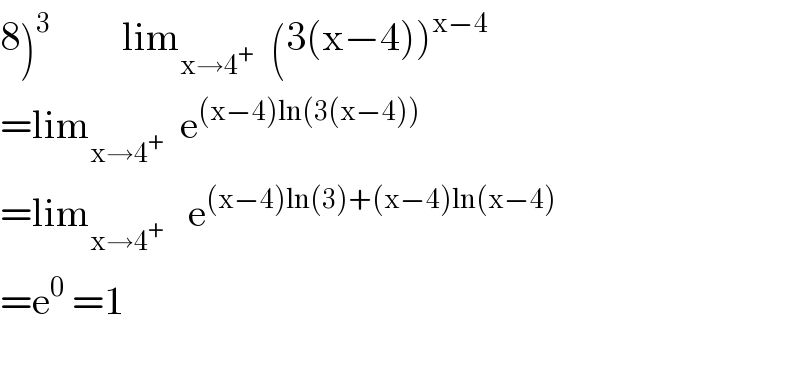
8)^3 lim_(x→4^+ ) (3(x−4))^(x−4) =lim_(x→4^+ ) e^((x−4)ln(3(x−4))) =lim_(x→4^+ ) e^((x−4)ln(3)+(x−4)ln(x−4)) =e^0 =1
$$\left.\mathrm{8}\right)^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}^{+} } \:\:\left(\mathrm{3}\left(\mathrm{x}−\mathrm{4}\right)\right)^{\mathrm{x}−\mathrm{4}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}^{+} } \:\:\mathrm{e}^{\left(\mathrm{x}−\mathrm{4}\right)\mathrm{ln}\left(\mathrm{3}\left(\mathrm{x}−\mathrm{4}\right)\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}^{+} } \:\:\:\mathrm{e}^{\left(\mathrm{x}−\mathrm{4}\right)\mathrm{ln}\left(\mathrm{3}\right)+\left(\mathrm{x}−\mathrm{4}\right)\mathrm{ln}\left(\mathrm{x}−\mathrm{4}\right)} \\ $$$$=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$$$ \\ $$
Answered by abdomathmax last updated on 07/Jun/20
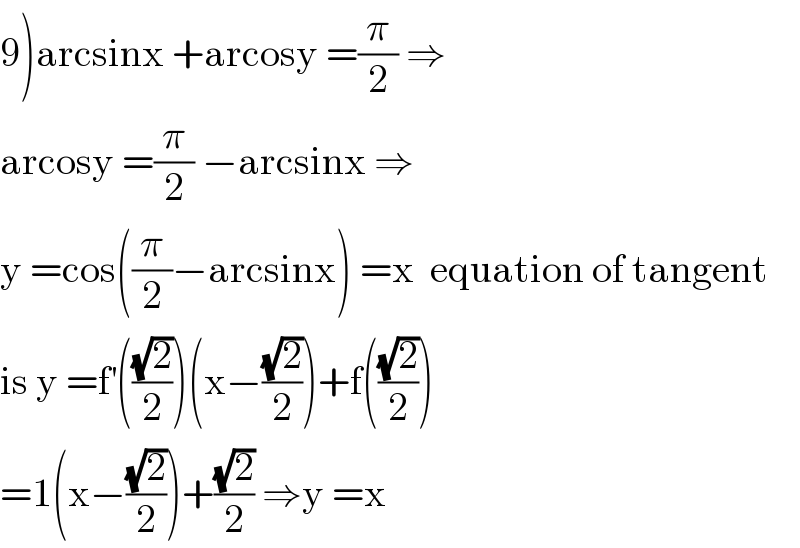
9)arcsinx +arcosy =(π/2) ⇒ arcosy =(π/2) −arcsinx ⇒ y =cos((π/2)−arcsinx) =x equation of tangent is y =f^′ (((√2)/2))(x−((√2)/2))+f(((√2)/2)) =1(x−((√2)/2))+((√2)/2) ⇒y =x
$$\left.\mathrm{9}\right)\mathrm{arcsinx}\:+\mathrm{arcosy}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{arcosy}\:=\frac{\pi}{\mathrm{2}}\:−\mathrm{arcsinx}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arcsinx}\right)\:=\mathrm{x}\:\:\mathrm{equation}\:\mathrm{of}\:\mathrm{tangent}\: \\ $$$$\mathrm{is}\:\mathrm{y}\:=\mathrm{f}^{'} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\left(\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\mathrm{f}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$=\mathrm{1}\left(\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\mathrm{y}\:=\mathrm{x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *