Question Number 97428 by bobhans last updated on 08/Jun/20
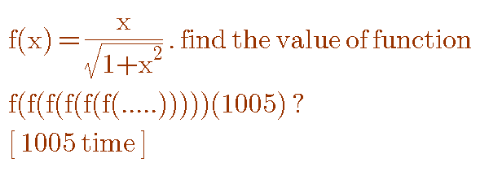
Commented by Farruxjano last updated on 08/Jun/20
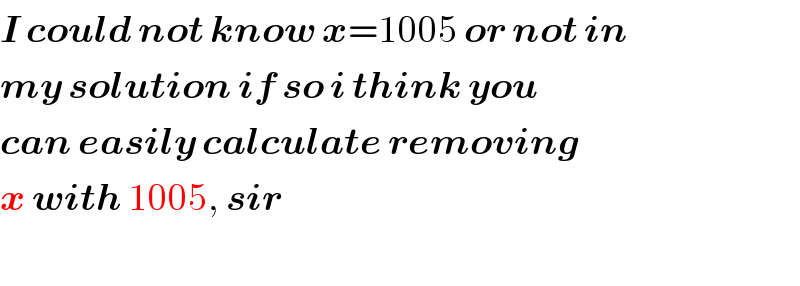
$$\boldsymbol{{I}}\:\boldsymbol{{could}}\:\boldsymbol{{not}}\:\boldsymbol{{know}}\:\boldsymbol{{x}}=\mathrm{1005}\:\boldsymbol{{or}}\:\boldsymbol{{not}}\:\boldsymbol{{in}} \\ $$$$\boldsymbol{{my}}\:\boldsymbol{{solution}}\:\boldsymbol{{if}}\:\boldsymbol{{so}}\:\boldsymbol{{i}}\:\boldsymbol{{think}}\:\boldsymbol{{you}} \\ $$$$\boldsymbol{{can}}\:\boldsymbol{{easily}}\:\boldsymbol{{calculate}}\:\boldsymbol{{removing}}\: \\ $$$$\boldsymbol{{x}}\:\boldsymbol{{with}}\:\mathrm{1005},\:\boldsymbol{{sir}} \\ $$$$ \\ $$
Commented by bobhans last updated on 08/Jun/20
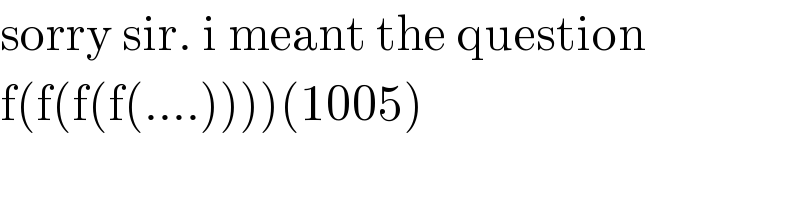
$$\mathrm{sorry}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{meant}\:\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{f}\left(\mathrm{f}\left(….\right)\right)\right)\right)\left(\mathrm{1005}\right) \\ $$
Commented by bemath last updated on 08/Jun/20
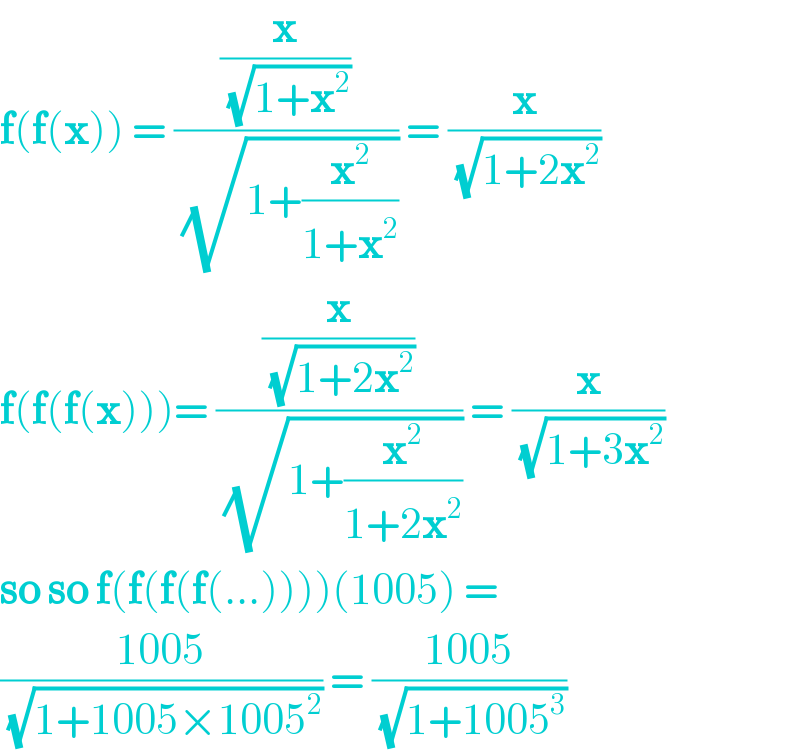
$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\right)\:=\:\frac{\frac{\boldsymbol{\mathrm{x}}}{\:\sqrt{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}+\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}}\:=\:\frac{\boldsymbol{\mathrm{x}}}{\:\sqrt{\mathrm{1}+\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\right)\right)=\:\frac{\frac{\boldsymbol{\mathrm{x}}}{\:\sqrt{\mathrm{1}+\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}+\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}}\:=\:\frac{\boldsymbol{\mathrm{x}}}{\:\sqrt{\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{f}}\left(…\right)\right)\right)\right)\left(\mathrm{1005}\right)\:= \\ $$$$\frac{\mathrm{1005}}{\:\sqrt{\mathrm{1}+\mathrm{1005}×\mathrm{1005}^{\mathrm{2}} }}\:=\:\frac{\mathrm{1005}}{\:\sqrt{\mathrm{1}+\mathrm{1005}^{\mathrm{3}} }} \\ $$
Commented by 1549442205 last updated on 08/Jun/20

$$\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{nice}\:\mathrm{greatly}!\mathrm{it}\:\mathrm{is}\:\mathrm{followed} \\ $$$$\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{argument} \\ $$
Commented by bobhans last updated on 08/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Farruxjano last updated on 08/Jun/20
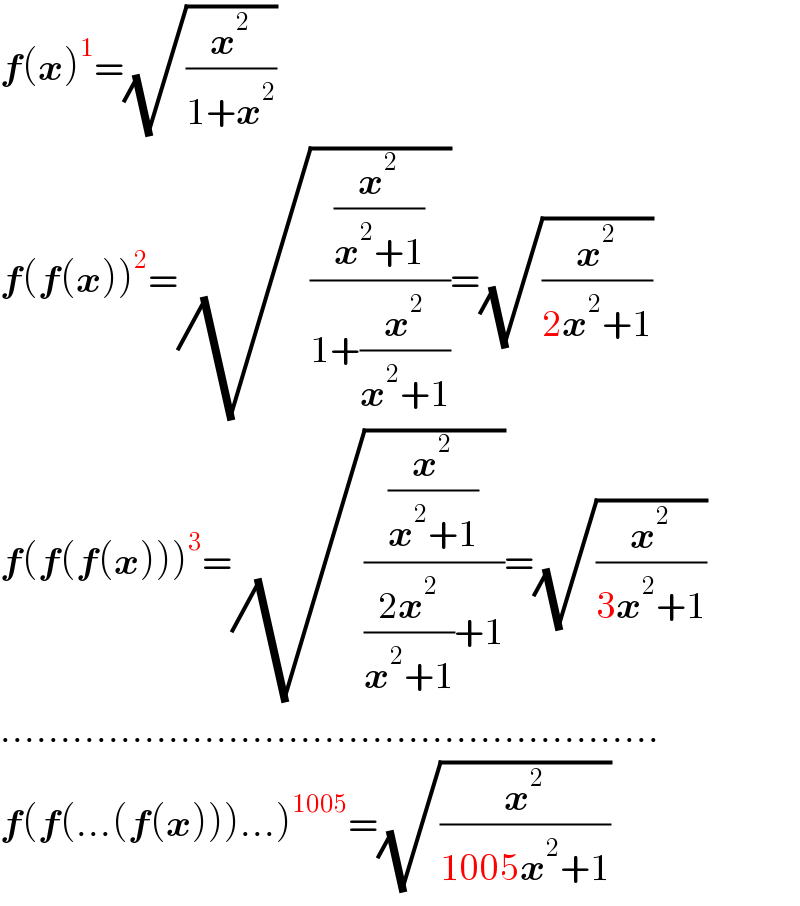
$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)^{\mathrm{1}} =\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}\: \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right)^{\mathrm{2}} =\sqrt{\frac{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{1}+\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}}=\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{f}}\left(\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right)\right)^{\mathrm{3}} =\sqrt{\frac{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}{\frac{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}}}=\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$………………………………………………. \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{f}}\left(…\left(\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right)\right)…\right)^{\mathrm{1005}} =\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{1005}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}} \\ $$
Answered by mathmax by abdo last updated on 08/Jun/20

$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\:=\mathrm{fof}\left(\mathrm{x}\right)\:=\frac{\mathrm{f}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{1}+\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)}}\:=\frac{\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}}\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{2x}^{\mathrm{2}} }} \\ $$$$\mathrm{let}\:\mathrm{suppose}\:\mathrm{f0f0}…\mathrm{0f}\left(\mathrm{x}\right)\left(\mathrm{ntime}\right)\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{nx}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\mathrm{fofof}…\mathrm{of}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{time}\:=\mathrm{f}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{nx}^{\mathrm{2}} }}\right)\:=\frac{\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{nx}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{nx}^{\mathrm{2}} }}}\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{the}\:\mathrm{relation}\:\mathrm{is}\:\mathrm{true}\:\mathrm{at}\:\mathrm{term}\left(\mathrm{n}+\mathrm{1}\right)\:\Rightarrow\mathrm{fofo}…\mathrm{of}\left(\mathrm{1005time}\right) \\ $$$$=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1006}\right)\mathrm{x}^{\mathrm{2}} }} \\ $$
Commented by mathmax by abdo last updated on 08/Jun/20
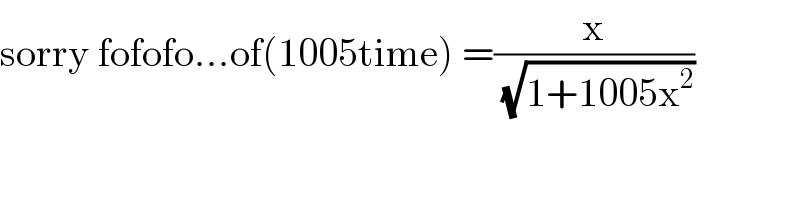
$$\mathrm{sorry}\:\mathrm{fofofo}…\mathrm{of}\left(\mathrm{1005time}\right)\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{1005x}^{\mathrm{2}} }} \\ $$
Commented by abdomathmax last updated on 08/Jun/20
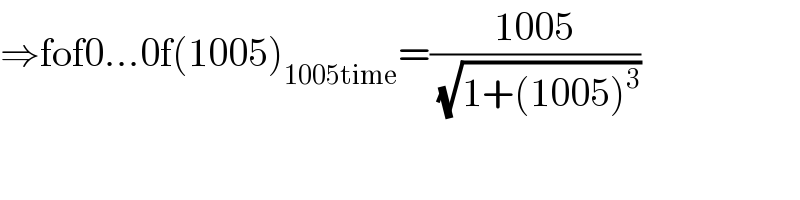
$$\Rightarrow\mathrm{fof0}…\mathrm{0f}\left(\mathrm{1005}\right)_{\mathrm{1005time}} =\frac{\mathrm{1005}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1005}\right)^{\mathrm{3}} }} \\ $$
