Question Number 97463 by john santu last updated on 08/Jun/20

Commented by bobhans last updated on 08/Jun/20
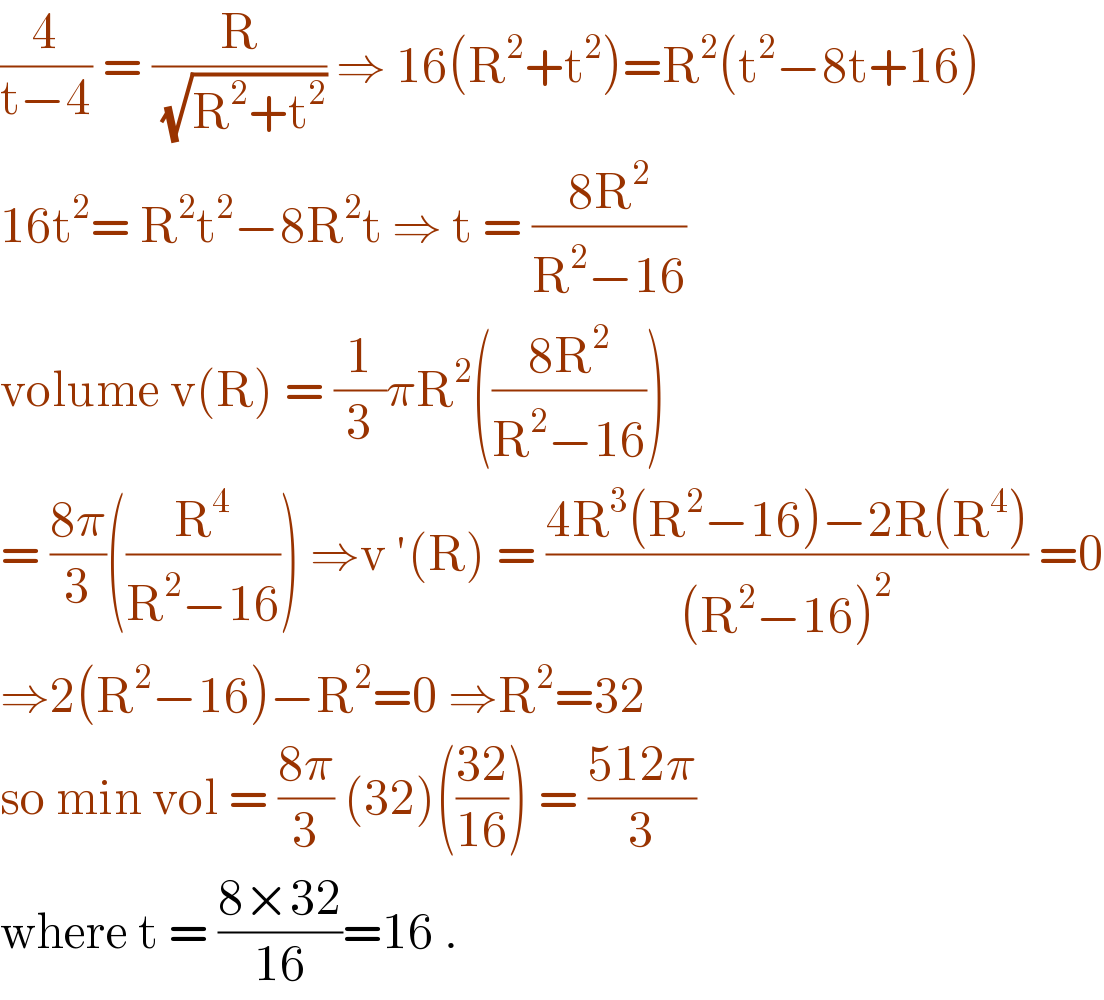
$$\frac{\mathrm{4}}{\mathrm{t}−\mathrm{4}}\:=\:\frac{\mathrm{R}}{\:\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\:\Rightarrow\:\mathrm{16}\left(\mathrm{R}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)=\mathrm{R}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} −\mathrm{8t}+\mathrm{16}\right) \\ $$$$\mathrm{16t}^{\mathrm{2}} =\:\mathrm{R}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} −\mathrm{8R}^{\mathrm{2}} \mathrm{t}\:\Rightarrow\:\mathrm{t}\:=\:\frac{\mathrm{8R}^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} −\mathrm{16}} \\ $$$$\mathrm{volume}\:\mathrm{v}\left(\mathrm{R}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\pi\mathrm{R}^{\mathrm{2}} \left(\frac{\mathrm{8R}^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} −\mathrm{16}}\right) \\ $$$$=\:\frac{\mathrm{8}\pi}{\mathrm{3}}\left(\frac{\mathrm{R}^{\mathrm{4}} }{\mathrm{R}^{\mathrm{2}} −\mathrm{16}}\right)\:\Rightarrow\mathrm{v}\:'\left(\mathrm{R}\right)\:=\:\frac{\mathrm{4R}^{\mathrm{3}} \left(\mathrm{R}^{\mathrm{2}} −\mathrm{16}\right)−\mathrm{2R}\left(\mathrm{R}^{\mathrm{4}} \right)}{\left(\mathrm{R}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{R}^{\mathrm{2}} −\mathrm{16}\right)−\mathrm{R}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{R}^{\mathrm{2}} =\mathrm{32} \\ $$$$\mathrm{so}\:\mathrm{min}\:\mathrm{vol}\:=\:\frac{\mathrm{8}\pi}{\mathrm{3}}\:\left(\mathrm{32}\right)\left(\frac{\mathrm{32}}{\mathrm{16}}\right)\:=\:\frac{\mathrm{512}\pi}{\mathrm{3}} \\ $$$$\mathrm{where}\:\mathrm{t}\:=\:\frac{\mathrm{8}×\mathrm{32}}{\mathrm{16}}=\mathrm{16}\:. \\ $$
Commented by john santu last updated on 08/Jun/20

$$\mathrm{yes}…\mathrm{correct} \\ $$
