Question Number 97555 by 175 last updated on 08/Jun/20

Commented by bemath last updated on 08/Jun/20
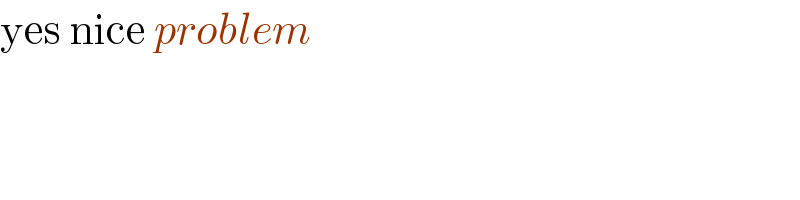
$$\mathrm{yes}\:\mathrm{nice}\:{problem}\: \\ $$
Commented by prakash jain last updated on 08/Jun/20

$${f}\left({x}\right)=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 08/Jun/20

$$\mathrm{nice}\:\mathrm{problem}\:\mathrm{and}\:\mathrm{nicefunction}\:\mathrm{and}\:\mathrm{nice}\:\mathrm{question}.. \\ $$
Commented by 175 last updated on 08/Jun/20
I want a non-static function
Commented by prakash jain last updated on 08/Jun/20

$${f}\left({x}\right)\:\mathrm{is}\:\mathbb{R}\rightarrow\mathbb{R}? \\ $$
Commented by MJS last updated on 08/Jun/20
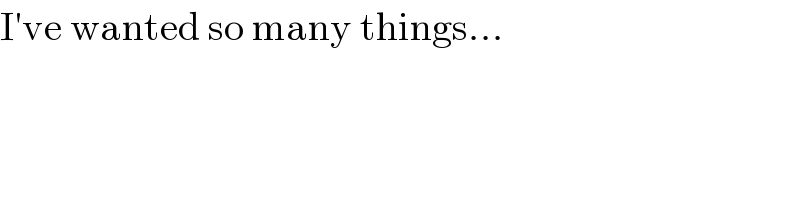
$$\mathrm{I}'\mathrm{ve}\:\mathrm{wanted}\:\mathrm{so}\:\mathrm{many}\:\mathrm{things}… \\ $$
Commented by bobhans last updated on 09/Jun/20

$$\mathrm{very}…\mathrm{nice} \\ $$
Commented by prakash jain last updated on 09/Jun/20

$$\mathrm{Hi}\:\mathrm{175}, \\ $$$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{specify}\:\mathrm{any} \\ $$$$\mathrm{additional}\:\mathrm{constraints}\:\mathrm{on}\:\mathrm{solution}. \\ $$$$\mathrm{A}\:\mathrm{non}-\mathrm{constant}\:\mathrm{solution}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{given}\:\mathrm{in}\:\mathrm{many}\:\mathrm{different}\:\mathrm{ways}. \\ $$$$\mathrm{Is}\:{f}\left({x}\right)\:\mathrm{continuous}? \\ $$$$\mathrm{Question}\:\mathrm{should}\:\mathrm{specify}. \\ $$
