Question-97557

Question Number 97557 by Power last updated on 08/Jun/20

Answered by mr W last updated on 08/Jun/20

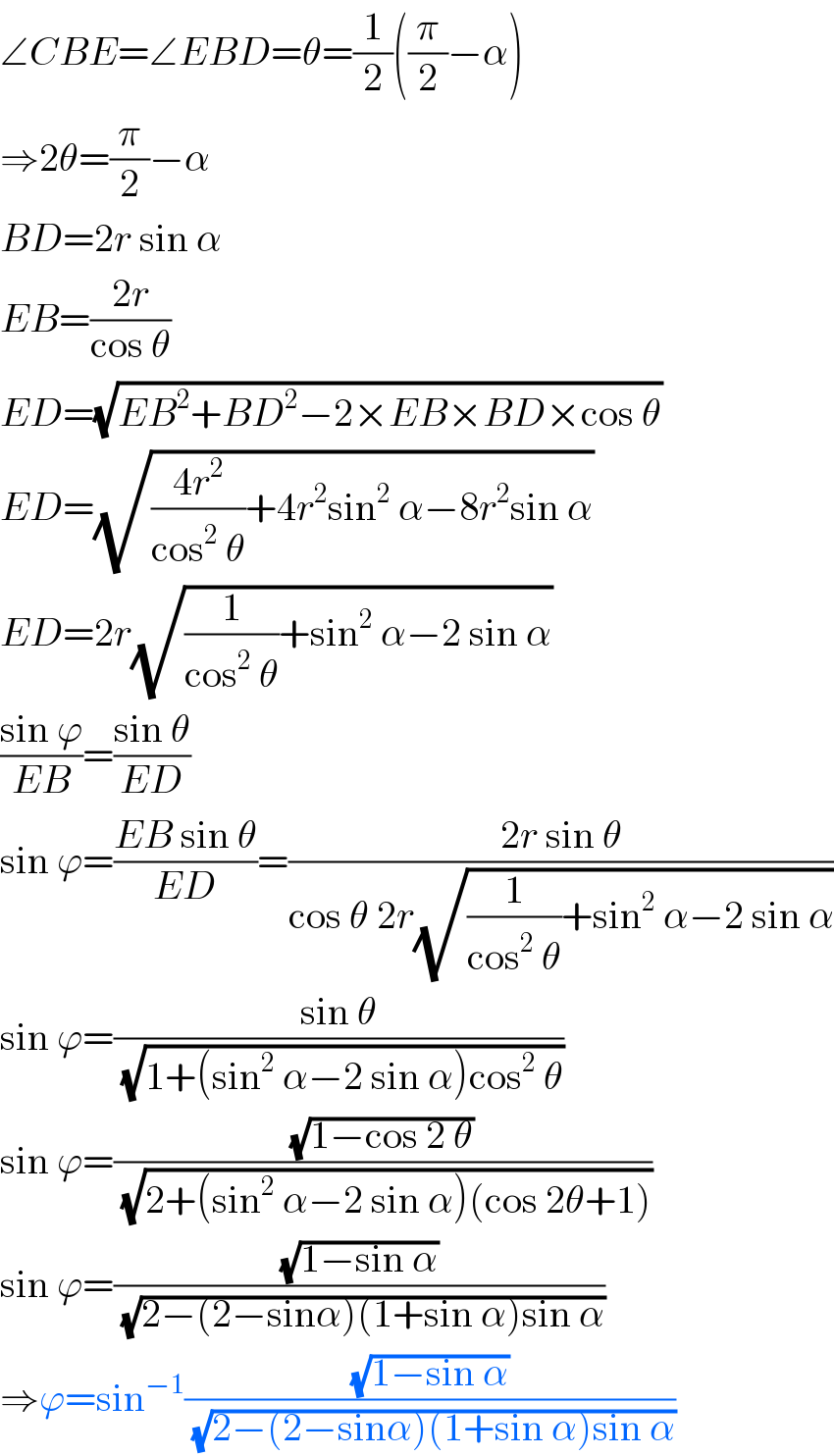
∠CBE=∠EBD=θ=(1/2)((π/2)−α) ⇒2θ=(π/2)−α BD=2r sin α EB=((2r)/(cos θ)) ED=(√(EB^2 +BD^2 −2×EB×BD×cos θ)) ED=(√(((4r^2 )/(cos^2 θ))+4r^2 sin^2 α−8r^2 sin α)) ED=2r(√((1/(cos^2 θ))+sin^2 α−2 sin α)) ((sin ϕ)/(EB))=((sin θ)/(ED)) sin ϕ=((EB sin θ)/(ED))=((2r sin θ)/(cos θ 2r(√((1/(cos^2 θ))+sin^2 α−2 sin α)))) sin ϕ=((sin θ)/( (√(1+(sin^2 α−2 sin α)cos^2 θ)))) sin ϕ=((√(1−cos 2 θ))/( (√(2+(sin^2 α−2 sin α)(cos 2θ+1))))) sin ϕ=((√(1−sin α))/( (√(2−(2−sinα)(1+sin α)sin α)))) ⇒ϕ=sin^(−1) ((√(1−sin α))/( (√(2−(2−sinα)(1+sin α)sin α))))

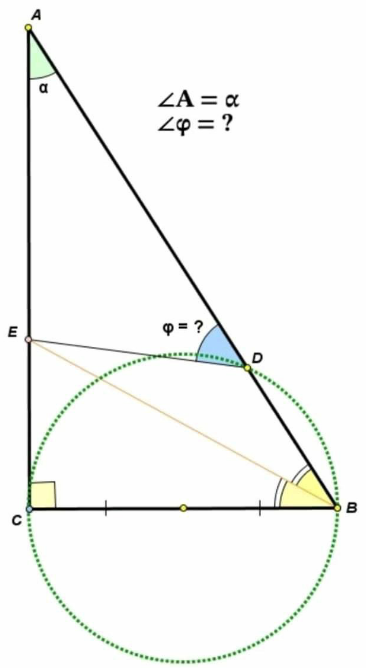
$$\angle{CBE}=\angle{EBD}=\theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\alpha\right) \\ $$$$\Rightarrow\mathrm{2}\theta=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$${BD}=\mathrm{2}{r}\:\mathrm{sin}\:\alpha \\ $$$${EB}=\frac{\mathrm{2}{r}}{\mathrm{cos}\:\theta} \\ $$$${ED}=\sqrt{{EB}^{\mathrm{2}} +{BD}^{\mathrm{2}} −\mathrm{2}×{EB}×{BD}×\mathrm{cos}\:\theta} \\ $$$${ED}=\sqrt{\frac{\mathrm{4}{r}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta}+\mathrm{4}{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{8}{r}^{\mathrm{2}} \mathrm{sin}\:\alpha} \\ $$$${ED}=\mathrm{2}{r}\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}+\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$$\frac{\mathrm{sin}\:\varphi}{{EB}}=\frac{\mathrm{sin}\:\theta}{{ED}} \\ $$$$\mathrm{sin}\:\varphi=\frac{{EB}\:\mathrm{sin}\:\theta}{{ED}}=\frac{\mathrm{2}{r}\:\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta\:\mathrm{2}{r}\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}+\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{2}\:\mathrm{sin}\:\alpha}} \\ $$$$\mathrm{sin}\:\varphi=\frac{\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{1}+\left(\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{2}\:\mathrm{sin}\:\alpha\right)\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\mathrm{sin}\:\varphi=\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\:\theta}}{\:\sqrt{\mathrm{2}+\left(\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{2}\:\mathrm{sin}\:\alpha\right)\left(\mathrm{cos}\:\mathrm{2}\theta+\mathrm{1}\right)}} \\ $$$$\mathrm{sin}\:\varphi=\frac{\sqrt{\mathrm{1}−\mathrm{sin}\:\alpha}}{\:\sqrt{\mathrm{2}−\left(\mathrm{2}−\mathrm{sin}\alpha\right)\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)\mathrm{sin}\:\alpha}} \\ $$$$\Rightarrow\varphi=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}−\mathrm{sin}\:\alpha}}{\:\sqrt{\mathrm{2}−\left(\mathrm{2}−\mathrm{sin}\alpha\right)\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)\mathrm{sin}\:\alpha}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply