Question Number 97660 by bobhans last updated on 09/Jun/20
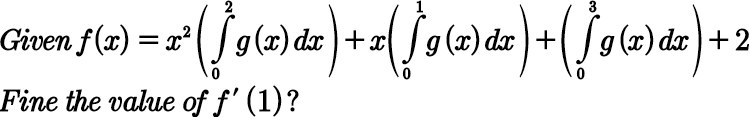
Commented by bemath last updated on 09/Jun/20

$$\mathrm{nice}\:\mathrm{question} \\ $$
Answered by bemath last updated on 09/Jun/20
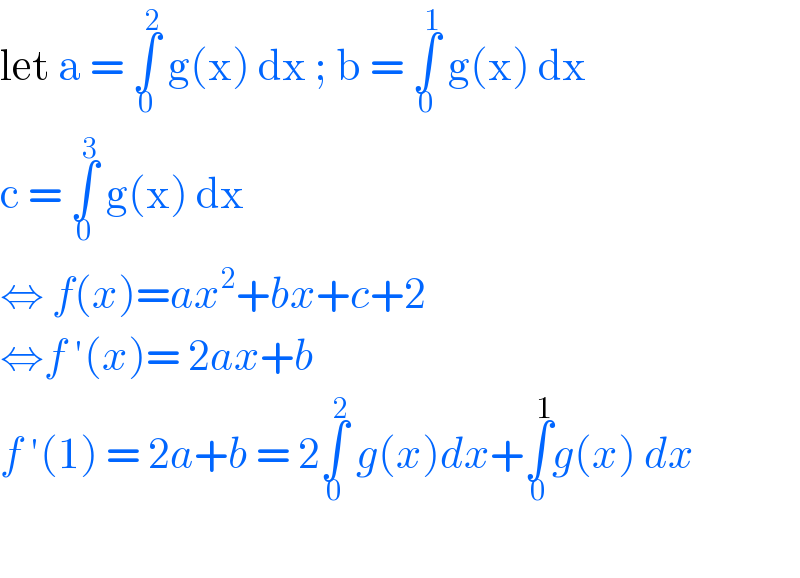
$$\mathrm{let}\:\mathrm{a}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{dx}\:;\:\mathrm{b}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{dx} \\ $$$$\mathrm{c}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{dx}\: \\ $$$$\Leftrightarrow\:{f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}+\mathrm{2} \\ $$$$\Leftrightarrow{f}\:'\left({x}\right)=\:\mathrm{2}{ax}+{b} \\ $$$${f}\:'\left(\mathrm{1}\right)\:=\:\mathrm{2}{a}+{b}\:=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{g}\left({x}\right){dx}+\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{g}\left({x}\right)\:{dx} \\ $$$$ \\ $$
Commented by bemath last updated on 09/Jun/20
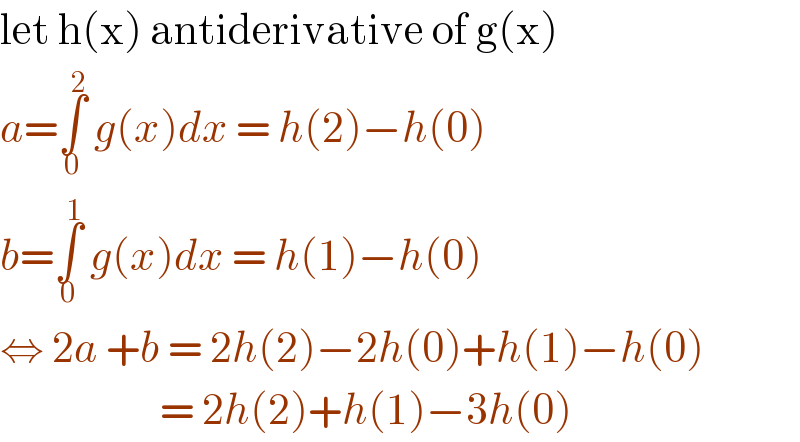
$$\mathrm{let}\:\mathrm{h}\left(\mathrm{x}\right)\:\mathrm{antiderivative}\:\mathrm{of}\:\mathrm{g}\left(\mathrm{x}\right) \\ $$$${a}=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{g}\left({x}\right){dx}\:=\:{h}\left(\mathrm{2}\right)−{h}\left(\mathrm{0}\right) \\ $$$${b}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{g}\left({x}\right){dx}\:=\:{h}\left(\mathrm{1}\right)−{h}\left(\mathrm{0}\right) \\ $$$$\Leftrightarrow\:\mathrm{2}{a}\:+{b}\:=\:\mathrm{2}{h}\left(\mathrm{2}\right)−\mathrm{2}{h}\left(\mathrm{0}\right)+{h}\left(\mathrm{1}\right)−{h}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{h}\left(\mathrm{2}\right)+{h}\left(\mathrm{1}\right)−\mathrm{3}{h}\left(\mathrm{0}\right) \\ $$
Answered by mathmax by abdo last updated on 09/Jun/20
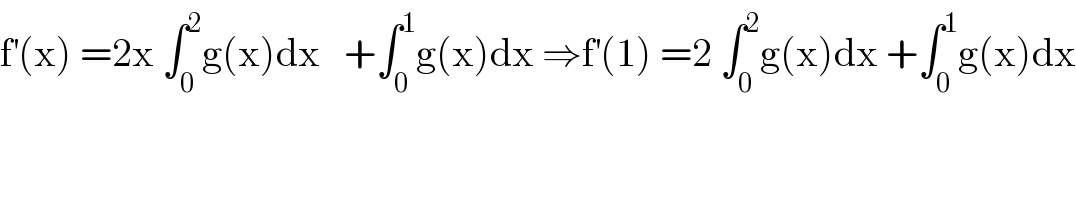
$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\mathrm{2x}\:\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\:\:\:+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{g}\left(\mathrm{x}\right)\mathrm{dx} \\ $$
