Question-97694

Question Number 97694 by mr W last updated on 09/Jun/20

Commented by Rio Michael last updated on 09/Jun/20

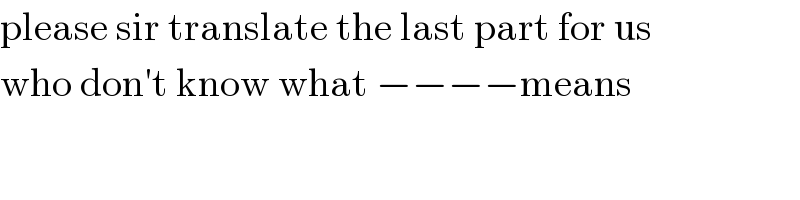
please sir translate the last part for us who don′t know what −−−−means

$$\mathrm{please}\:\mathrm{sir}\:\mathrm{translate}\:\mathrm{the}\:\mathrm{last}\:\mathrm{part}\:\mathrm{for}\:\mathrm{us} \\ $$$$\mathrm{who}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{what}\:−−−−\mathrm{means} \\ $$

Commented by mr W last updated on 09/Jun/20

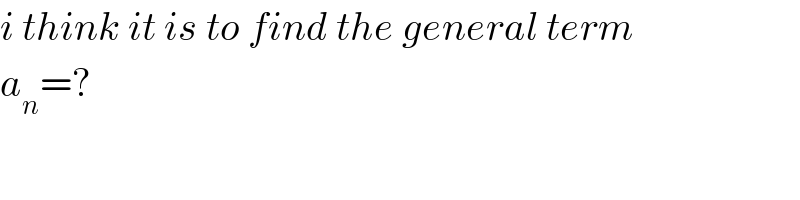
$${i}\:{think}\:{it}\:{is}\:{to}\:{find}\:{the}\:{general}\:{term} \\ $$$${a}_{{n}} =? \\ $$

Commented by prakash jain last updated on 09/Jun/20

a_(n+1) −3a_n =6n^2 −12n+2 a_(n+1) −3a_n =f(n) Linear non−homogeneous equation. homogeneous solution λ−3=0⇒a_n =c3^n Particular solution g(n) since it is linear g(n) will be similar to f(n) g(n)=bn^2 +cn+d b(n+1)^2 +c(n+1)+d−3(bn^2 +cn+d)= 6n^2 −12n+2 b−3b=6⇒b=−3 2b+c−3c=−12 −2c=−12−2b=−6⇒c=3 b+c+d−3d=2 −3+3−2d=2⇒d=−1 g(n)=−3n^2 +3n−1 general solution a(n)=c3^n −3n^2 +3n−1

$${a}_{{n}+\mathrm{1}} −\mathrm{3}{a}_{{n}} =\mathrm{6}{n}^{\mathrm{2}} −\mathrm{12}{n}+\mathrm{2} \\ $$$${a}_{{n}+\mathrm{1}} −\mathrm{3}{a}_{{n}} ={f}\left({n}\right) \\ $$$$\mathrm{Linear}\:\mathrm{non}−\mathrm{homogeneous}\:\mathrm{equation}. \\ $$$$\mathrm{homogeneous}\:\mathrm{solution} \\ $$$$\lambda−\mathrm{3}=\mathrm{0}\Rightarrow{a}_{{n}} ={c}\mathrm{3}^{{n}} \\ $$$$\mathrm{Particular}\:\mathrm{solution}\:{g}\left({n}\right) \\ $$$$\mathrm{since}\:\mathrm{it}\:\mathrm{is}\:\mathrm{linear}\:{g}\left({n}\right)\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{similar}\:\mathrm{to}\:\mathrm{f}\left(\mathrm{n}\right) \\ $$$${g}\left({n}\right)={bn}^{\mathrm{2}} +{cn}+{d} \\ $$$${b}\left({n}+\mathrm{1}\right)^{\mathrm{2}} +{c}\left({n}+\mathrm{1}\right)+{d}−\mathrm{3}\left({bn}^{\mathrm{2}} +{cn}+{d}\right)= \\ $$$$\:\:\:\:\:\mathrm{6}{n}^{\mathrm{2}} −\mathrm{12}{n}+\mathrm{2} \\ $$$${b}−\mathrm{3}{b}=\mathrm{6}\Rightarrow{b}=−\mathrm{3} \\ $$$$\mathrm{2}{b}+{c}−\mathrm{3}{c}=−\mathrm{12} \\ $$$$−\mathrm{2}{c}=−\mathrm{12}−\mathrm{2}{b}=−\mathrm{6}\Rightarrow{c}=\mathrm{3} \\ $$$${b}+{c}+{d}−\mathrm{3}{d}=\mathrm{2} \\ $$$$−\mathrm{3}+\mathrm{3}−\mathrm{2}{d}=\mathrm{2}\Rightarrow{d}=−\mathrm{1} \\ $$$${g}\left({n}\right)=−\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1} \\ $$$${general}\:{solution} \\ $$$${a}\left({n}\right)={c}\mathrm{3}^{{n}} −\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1} \\ $$

Commented by john santu last updated on 11/Jun/20

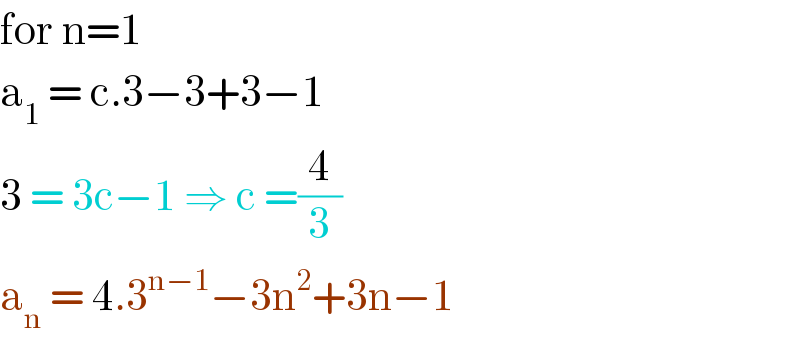
for n=1 a_1 = c.3−3+3−1 3 = 3c−1 ⇒ c =(4/3) a_n = 4.3^(n−1) −3n^2 +3n−1

$$\mathrm{for}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{1}} \:=\:\mathrm{c}.\mathrm{3}−\mathrm{3}+\mathrm{3}−\mathrm{1} \\ $$$$\mathrm{3}\:=\:\mathrm{3c}−\mathrm{1}\:\Rightarrow\:\mathrm{c}\:=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{a}_{\mathrm{n}} \:=\:\mathrm{4}.\mathrm{3}^{\mathrm{n}−\mathrm{1}} −\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}−\mathrm{1} \\ $$

Commented by mr W last updated on 09/Jun/20

$${thanks}\:{for}\:{solving}! \\ $$

Commented by I want to learn more last updated on 10/Jun/20

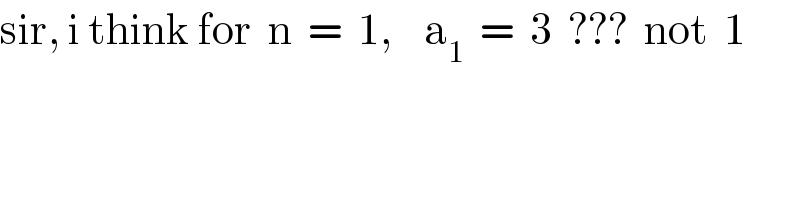
sir, i think for n = 1, a_1 = 3 ??? not 1

$$\mathrm{sir},\:\mathrm{i}\:\mathrm{think}\:\mathrm{for}\:\:\mathrm{n}\:\:=\:\:\mathrm{1},\:\:\:\:\mathrm{a}_{\mathrm{1}} \:\:=\:\:\mathrm{3}\:\:???\:\:\mathrm{not}\:\:\mathrm{1} \\ $$

Commented by mr W last updated on 10/Jun/20

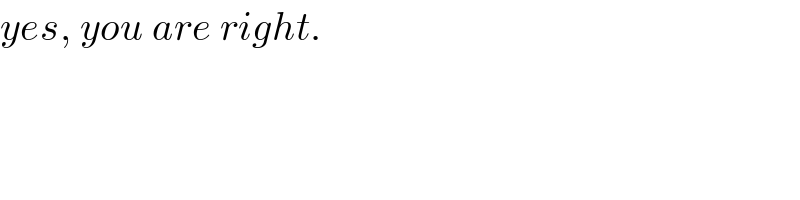
$${yes},\:{you}\:{are}\:{right}. \\ $$

Answered by mathmax by abdo last updated on 09/Jun/20

$$\mathrm{perhaps}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\mathrm{find}\:\mathrm{a}_{\mathrm{n}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply