Question Number 97721 by Power last updated on 09/Jun/20
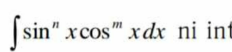
Commented by mr W last updated on 09/Jun/20

Commented by smridha last updated on 09/Jun/20

$${this}\:{is}\:{not}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}!!! \\ $$
Commented by mr W last updated on 09/Jun/20

$${wow},\:\:{red}\:{bold}\:{text}\:{with}\:{three} \\ $$$${exclamation}\:{marks}! \\ $$
Answered by smridha last updated on 09/Jun/20

$$\boldsymbol{{let}}\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{u}}\:\boldsymbol{{so}} \\ $$$$\int\left(\mathrm{1}−\boldsymbol{{u}}^{\mathrm{2}} \right)^{\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} \boldsymbol{{u}}^{\boldsymbol{{n}}} \boldsymbol{{du}} \\ $$$$=\int\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\frac{\left({m}−\mathrm{1}\right)}{\mathrm{2}}} {\sum}}\overset{\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} {{C}}_{\boldsymbol{{r}}} \left(\mathrm{1}\right)^{\boldsymbol{{r}}−\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} .\left(−\mathrm{1}\right)^{\boldsymbol{{r}}} \boldsymbol{{u}}^{\mathrm{2}\boldsymbol{{r}}} \boldsymbol{{u}}^{\boldsymbol{{n}}} \boldsymbol{{du}} \\ $$$$=\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{\boldsymbol{{r}}} .\overset{\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} {\boldsymbol{{C}}}_{\boldsymbol{{r}}} \frac{\left(\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\right)^{\mathrm{2}\boldsymbol{{r}}+\boldsymbol{{n}}+\mathrm{1}} }{\left(\mathrm{2}\boldsymbol{{r}}+\boldsymbol{{n}}+\mathrm{1}\right)}\:+\boldsymbol{{g}} \\ $$
Commented by Power last updated on 09/Jun/20

$$\mathrm{Brilliant}\:!\:\:\:\mathrm{I}\:\mathrm{would}\:\mathrm{be}\:\mathrm{glad}\:\mathrm{if}\:\mathrm{you}\:\mathrm{give}\:\mathrm{me}\:\mathrm{an}\:\mathrm{idea} \\ $$
Commented by smridha last updated on 09/Jun/20

$$\boldsymbol{{about}}\:\boldsymbol{{what}}? \\ $$
Commented by Power last updated on 09/Jun/20

$$\mathrm{solution} \\ $$
Commented by smridha last updated on 09/Jun/20

$${at}\:\boldsymbol{{first}}\:\boldsymbol{{I}}\:\boldsymbol{{B}}{i}\boldsymbol{{nomially}}\:\boldsymbol{{expand}} \\ $$$$\left(\mathrm{1}−\boldsymbol{{u}}^{\mathrm{2}} \right)^{\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right)}{\mathrm{2}}} \:\boldsymbol{{then}}\:\boldsymbol{{i}}\:\boldsymbol{{interchanged}} \\ $$$$\boldsymbol{{summation}}\:\boldsymbol{{and}}\:\boldsymbol{{integration}} \\ $$$$\boldsymbol{{because}}\:\boldsymbol{{the}}\:\boldsymbol{{integrand}}\:\boldsymbol{{function}} \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{uniformly}}\:\boldsymbol{{convergent}}…. \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{you}}\:\boldsymbol{{also}}\:\boldsymbol{{check}}\:\boldsymbol{{this}}\:\boldsymbol{{by}}\:\boldsymbol{{putting}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{m}}\:\boldsymbol{{and}}\:\boldsymbol{{n}}\:\boldsymbol{{as}}\:\boldsymbol{{your}}\:\boldsymbol{{wish}} \\ $$
Commented by Power last updated on 09/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
