Question Number 97752 by Power last updated on 09/Jun/20

Commented by mr W last updated on 09/Jun/20

$${i}\:{got}\:{x}=\mathrm{1} \\ $$$$\left.\Rightarrow{Answer}\:{B}\right) \\ $$
Commented by Power last updated on 09/Jun/20

$$\mathrm{sir}\:\mathrm{please}\:\mathrm{solution} \\ $$
Commented by Algoritm last updated on 09/Jun/20

$${prove}\:{that}\:{sir}\: \\ $$
Commented by Farruxjano last updated on 09/Jun/20

$$\mathrm{I}\:\mathrm{got}\:\mathrm{either}.\:\mathrm{My}\:\mathrm{ans}\:\mathrm{is}\:\mathrm{x}=\mathrm{1}\:\mathrm{too}. \\ $$
Answered by Farruxjano last updated on 09/Jun/20
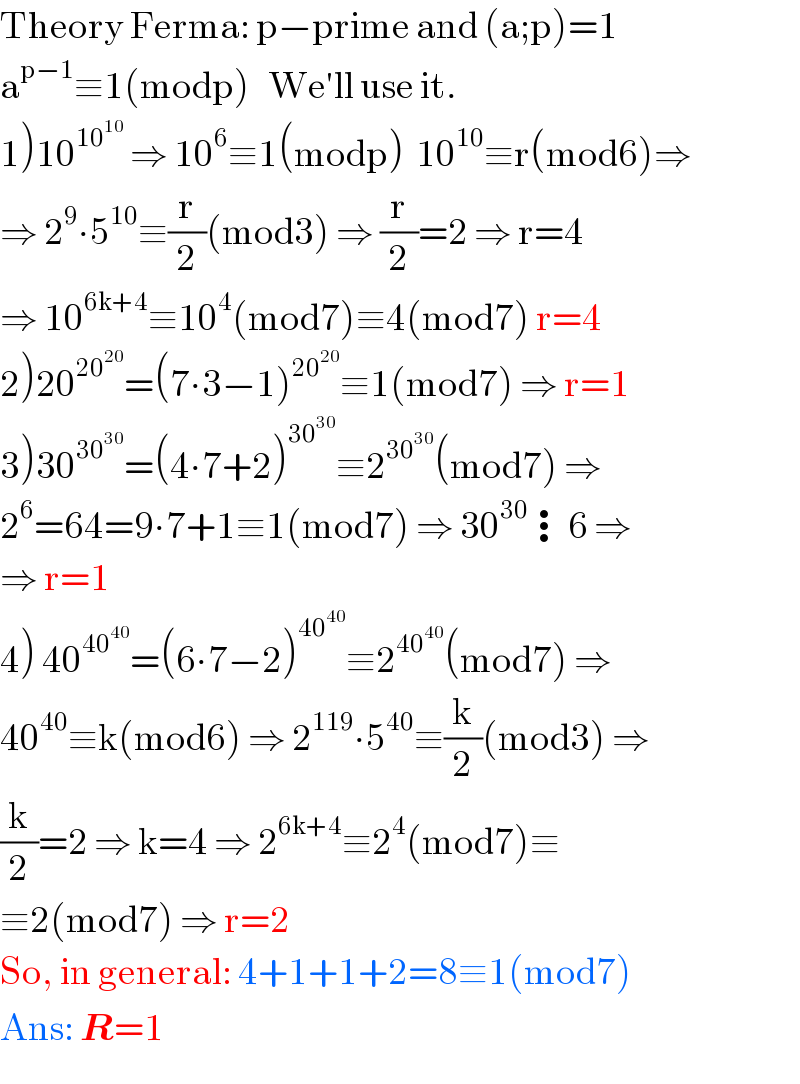
$$\mathrm{Theory}\:\mathrm{Ferma}:\:\mathrm{p}−\mathrm{prime}\:\mathrm{and}\:\left(\mathrm{a};\mathrm{p}\right)=\mathrm{1} \\ $$$$\mathrm{a}^{\mathrm{p}−\mathrm{1}} \equiv\mathrm{1}\left(\mathrm{modp}\right)\:\:\:\mathrm{We}'\mathrm{ll}\:\mathrm{use}\:\mathrm{it}. \\ $$$$\left.\mathrm{1}\right)\mathrm{10}^{\mathrm{10}^{\mathrm{10}} } \:\Rightarrow\:\mathrm{10}^{\mathrm{6}} \equiv\mathrm{1}\left(\mathrm{modp}\right)\:\:\mathrm{10}^{\mathrm{10}} \equiv\mathrm{r}\left(\mathrm{mod6}\right)\Rightarrow \\ $$$$\Rightarrow\:\mathrm{2}^{\mathrm{9}} \centerdot\mathrm{5}^{\mathrm{10}} \equiv\frac{\mathrm{r}}{\mathrm{2}}\left(\mathrm{mod3}\right)\:\Rightarrow\:\frac{\mathrm{r}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow\:\mathrm{r}=\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{10}^{\mathrm{6k}+\mathrm{4}} \equiv\mathrm{10}^{\mathrm{4}} \left(\mathrm{mod7}\right)\equiv\mathrm{4}\left(\mathrm{mod7}\right)\:\mathrm{r}=\mathrm{4} \\ $$$$\left.\mathrm{2}\right)\mathrm{20}^{\mathrm{20}^{\mathrm{20}} } =\left(\mathrm{7}\centerdot\mathrm{3}−\mathrm{1}\right)^{\mathrm{20}^{\mathrm{20}} } \equiv\mathrm{1}\left(\mathrm{mod7}\right)\:\Rightarrow\:\mathrm{r}=\mathrm{1} \\ $$$$\left.\mathrm{3}\right)\mathrm{30}^{\mathrm{30}^{\mathrm{30}} } =\left(\mathrm{4}\centerdot\mathrm{7}+\mathrm{2}\right)^{\mathrm{30}^{\mathrm{30}} } \equiv\mathrm{2}^{\mathrm{30}^{\mathrm{30}} } \left(\mathrm{mod7}\right)\:\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{6}} =\mathrm{64}=\mathrm{9}\centerdot\mathrm{7}+\mathrm{1}\equiv\mathrm{1}\left(\mathrm{mod7}\right)\:\Rightarrow\:\mathrm{30}^{\mathrm{30}} \vdots\mathrm{6}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{r}=\mathrm{1} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{40}^{\mathrm{40}^{\mathrm{40}} } =\left(\mathrm{6}\centerdot\mathrm{7}−\mathrm{2}\right)^{\mathrm{40}^{\mathrm{40}} } \equiv\mathrm{2}^{\mathrm{40}^{\mathrm{40}} } \left(\mathrm{mod7}\right)\:\Rightarrow \\ $$$$\mathrm{40}^{\mathrm{40}} \equiv\mathrm{k}\left(\mathrm{mod6}\right)\:\Rightarrow\:\mathrm{2}^{\mathrm{119}} \centerdot\mathrm{5}^{\mathrm{40}} \equiv\frac{\mathrm{k}}{\mathrm{2}}\left(\mathrm{mod3}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{k}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow\:\mathrm{k}=\mathrm{4}\:\Rightarrow\:\mathrm{2}^{\mathrm{6k}+\mathrm{4}} \equiv\mathrm{2}^{\mathrm{4}} \left(\mathrm{mod7}\right)\equiv \\ $$$$\equiv\mathrm{2}\left(\mathrm{mod7}\right)\:\Rightarrow\:\mathrm{r}=\mathrm{2} \\ $$$$\mathrm{So},\:\mathrm{in}\:\mathrm{general}:\:\mathrm{4}+\mathrm{1}+\mathrm{1}+\mathrm{2}=\mathrm{8}\equiv\mathrm{1}\left(\mathrm{mod7}\right) \\ $$$$\mathrm{Ans}:\:\boldsymbol{{R}}=\mathrm{1} \\ $$
Commented by Algoritm last updated on 09/Jun/20

$$\mathrm{super}! \\ $$
Commented by mr W last updated on 09/Jun/20

$${nice}\:{solution}\:{sir}! \\ $$
