Question Number 97901 by pranesh last updated on 10/Jun/20
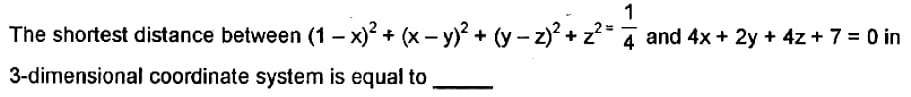
Commented by pranesh last updated on 10/Jun/20

$${solve}\:{fast}\:{please} \\ $$
Commented by prakash jain last updated on 10/Jun/20

$$\mathrm{Question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear}.\:\mathrm{Please}\:\mathrm{edit}\:\mathrm{image} \\ $$$$\mathrm{and}\:\mathrm{upload}\:\mathrm{again}? \\ $$
Answered by mr W last updated on 11/Jun/20
![METHOD I say plane touching the surface is 2x+y+2z+2k=0 ⇒y=−2(x+z+k) (1−x)^2 +(x−y)^2 +(y−z)^2 +z^2 =(1/4) (1−x)^2 +(3x+2z+2k)^2 +(2x+3z+2k)^2 +z^2 −(1/4)=0 1−2x+x^2 +9x^2 +4z^2 +4k^2 +12xz+12kx+8kz+4x^2 +9z^2 +4k^2 +12xz+8kx+12kz+z^2 −(1/4)=0 14x^2 +14z^2 +24xz+2(10k−1)x+20kz+8k^2 +(3/4)=0 ⇒7x^2 +7z^2 +12xz+(10k−1)x+10kz+4k^2 +(3/8)=0 7z^2 +(12x+10k)z+7x^2 +(10k−1)x+4k^2 +(3/8)=0 Δ=(12x+10k)^2 −4×7[7x^2 +(10k−1)x+4k^2 +(3/8)]=0 (6x+5k)^2 −7[7x^2 +(10k−1)x+4k^2 +(3/8)]=0 ⇒13x^2 +(10k−7)x+3k^2 +((21)/8)=0 Δ=(10k−7)^2 −4×13(3k^2 +((21)/8))=0 ⇒112k^2 +280k+175=0 ⇒k=−(5/4) distance between the planes 4x+2y+4z−5=0 4x+2y+4z+7=0 is d=((7−(−5))/( (√(4^2 +2^2 +4^2 ))))=2 that′s the shortest distance.](https://www.tinkutara.com/question/Q98026.png)
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${say}\:{plane}\:{touching}\:{the}\:{surface}\:{is} \\ $$$$\mathrm{2}{x}+{y}+\mathrm{2}{z}+\mathrm{2}{k}=\mathrm{0} \\ $$$$\Rightarrow{y}=−\mathrm{2}\left({x}+{z}+{k}\right) \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left(\mathrm{3}{x}+\mathrm{2}{z}+\mathrm{2}{k}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}+\mathrm{3}{z}+\mathrm{2}{k}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}{z}^{\mathrm{2}} +\mathrm{4}{k}^{\mathrm{2}} +\mathrm{12}{xz}+\mathrm{12}{kx}+\mathrm{8}{kz}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{9}{z}^{\mathrm{2}} +\mathrm{4}{k}^{\mathrm{2}} +\mathrm{12}{xz}+\mathrm{8}{kx}+\mathrm{12}{kz}+{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{14}{x}^{\mathrm{2}} +\mathrm{14}{z}^{\mathrm{2}} +\mathrm{24}{xz}+\mathrm{2}\left(\mathrm{10}{k}−\mathrm{1}\right){x}+\mathrm{20}{kz}+\mathrm{8}{k}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{7}{x}^{\mathrm{2}} +\mathrm{7}{z}^{\mathrm{2}} +\mathrm{12}{xz}+\left(\mathrm{10}{k}−\mathrm{1}\right){x}+\mathrm{10}{kz}+\mathrm{4}{k}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{7}{z}^{\mathrm{2}} +\left(\mathrm{12}{x}+\mathrm{10}{k}\right){z}+\mathrm{7}{x}^{\mathrm{2}} +\left(\mathrm{10}{k}−\mathrm{1}\right){x}+\mathrm{4}{k}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{12}{x}+\mathrm{10}{k}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{7}\left[\mathrm{7}{x}^{\mathrm{2}} +\left(\mathrm{10}{k}−\mathrm{1}\right){x}+\mathrm{4}{k}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}\right]=\mathrm{0} \\ $$$$\left(\mathrm{6}{x}+\mathrm{5}{k}\right)^{\mathrm{2}} −\mathrm{7}\left[\mathrm{7}{x}^{\mathrm{2}} +\left(\mathrm{10}{k}−\mathrm{1}\right){x}+\mathrm{4}{k}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{13}{x}^{\mathrm{2}} +\left(\mathrm{10}{k}−\mathrm{7}\right){x}+\mathrm{3}{k}^{\mathrm{2}} +\frac{\mathrm{21}}{\mathrm{8}}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{10}{k}−\mathrm{7}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{13}\left(\mathrm{3}{k}^{\mathrm{2}} +\frac{\mathrm{21}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{112}{k}^{\mathrm{2}} +\mathrm{280}{k}+\mathrm{175}=\mathrm{0} \\ $$$$\Rightarrow{k}=−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$ \\ $$$${distance}\:{between}\:{the}\:{planes} \\ $$$$\mathrm{4}{x}+\mathrm{2}{y}+\mathrm{4}{z}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{4}{x}+\mathrm{2}{y}+\mathrm{4}{z}+\mathrm{7}=\mathrm{0} \\ $$$${is} \\ $$$${d}=\frac{\mathrm{7}−\left(−\mathrm{5}\right)}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }}=\mathrm{2} \\ $$$${that}'{s}\:{the}\:{shortest}\:{distance}. \\ $$
Answered by mr W last updated on 11/Jun/20
![METHOD II d=((4x+2y+4z+7)/( (√(4^2 +2^2 +4^2 ))))=(1/3)(2x+y+2z+(7/2)) it′s to find the minimum of f(x,y,z)=2x+y+2z with (1−x)^2 +(x−y)^2 +(y−z)^2 +z^2 −(1/4)=0 F=2x+y+2z+λ[(1−x)^2 +(x−y)^2 +(y−z)^2 +z^2 −(1/4)] (∂F/∂x)=2+λ[−2(1−x)+2(x−y)]=0 ⇒1+λ(−1+2x−y)=0 ⇒2x−y−1=−(1/λ) ...(i) (∂F/∂y)=1+λ[−2(x−y)+2(y−z)]=0 ⇒1+2λ(−x+2y−z)=0 ⇒2(−x+2y−z)=−(1/λ) ...(ii) (∂F/∂z)=2+λ[−2(y−z)+2z]=0 ⇒1+λ(−y+2z)=0 ⇒−y+2z=−(1/λ) ...(iii) y=((6z+1)/5) x=z+(1/2) ((1/2)−z)^2 +((3/(10))−(z/5))^2 +((z/5)+(1/5))^2 +z^2 −(1/4)=0 4z^2 −2z+(1/4)=0 (2z−(1/2))^2 =0 ⇒z=(1/4) ⇒x=(3/4) ⇒y=(1/5)((6/4)+1)=(1/2) d=(1/3)(2×(3/4)+(1/2)+2×(1/4)+(7/2))=2](https://www.tinkutara.com/question/Q98074.png)
$$\boldsymbol{{METHOD}}\:\boldsymbol{{II}} \\ $$$${d}=\frac{\mathrm{4}{x}+\mathrm{2}{y}+\mathrm{4}{z}+\mathrm{7}}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{x}+{y}+\mathrm{2}{z}+\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$${it}'{s}\:{to}\:{find}\:{the}\:{minimum}\:{of} \\ $$$${f}\left({x},{y},{z}\right)=\mathrm{2}{x}+{y}+\mathrm{2}{z}\:{with} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$${F}=\mathrm{2}{x}+{y}+\mathrm{2}{z}+\lambda\left[\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right] \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{2}+\lambda\left[−\mathrm{2}\left(\mathrm{1}−{x}\right)+\mathrm{2}\left({x}−{y}\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+\lambda\left(−\mathrm{1}+\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}−{y}−\mathrm{1}=−\frac{\mathrm{1}}{\lambda}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{F}}{\partial{y}}=\mathrm{1}+\lambda\left[−\mathrm{2}\left({x}−{y}\right)+\mathrm{2}\left({y}−{z}\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}\lambda\left(−{x}+\mathrm{2}{y}−{z}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left(−{x}+\mathrm{2}{y}−{z}\right)=−\frac{\mathrm{1}}{\lambda}\:\:\:…\left({ii}\right) \\ $$$$\frac{\partial{F}}{\partial{z}}=\mathrm{2}+\lambda\left[−\mathrm{2}\left({y}−{z}\right)+\mathrm{2}{z}\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+\lambda\left(−{y}+\mathrm{2}{z}\right)=\mathrm{0} \\ $$$$\Rightarrow−{y}+\mathrm{2}{z}=−\frac{\mathrm{1}}{\lambda}\:\:…\left({iii}\right) \\ $$$${y}=\frac{\mathrm{6}{z}+\mathrm{1}}{\mathrm{5}} \\ $$$${x}={z}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−{z}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{10}}−\frac{{z}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{{z}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{4}{z}^{\mathrm{2}} −\mathrm{2}{z}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left(\mathrm{2}{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{5}}\left(\frac{\mathrm{6}}{\mathrm{4}}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${d}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{7}}{\mathrm{2}}\right)=\mathrm{2} \\ $$
