Question Number 97942 by pranesh last updated on 10/Jun/20
Answered by john santu last updated on 10/Jun/20
Answered by Aniruddha Ghosh last updated on 10/Jun/20

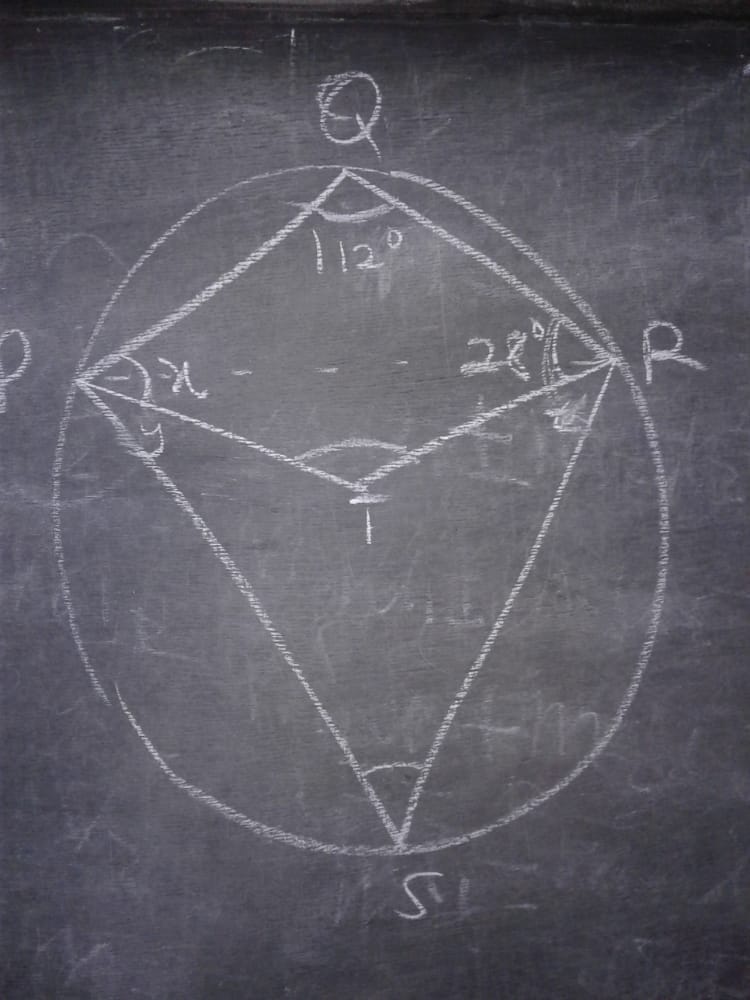
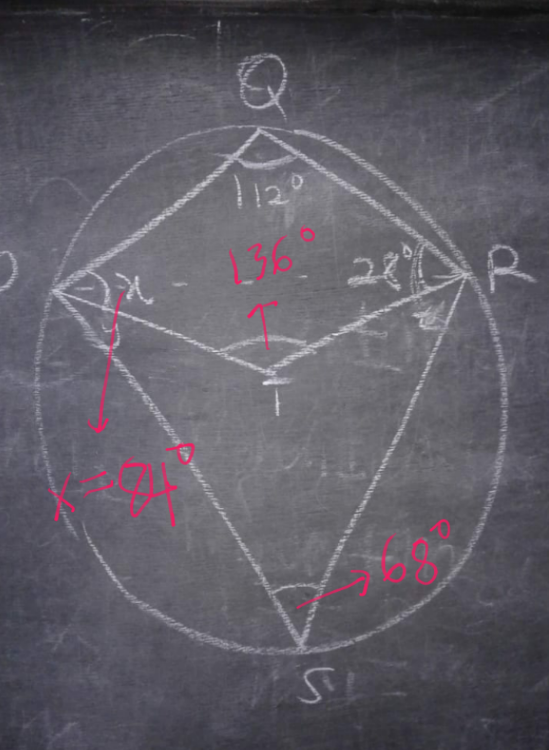
$$\boldsymbol{\mathrm{PQRS}}\:\mathrm{is}\:\mathrm{a}\:\boldsymbol{\mathrm{circular}}\:\boldsymbol{\mathrm{quadrilateral}}. \\ $$$$\angle\boldsymbol{\mathrm{PQR}}\:=\:\mathrm{180}°−\:\angle\boldsymbol{\mathrm{PSR}} \\ $$$$\:\:\:\:\therefore\:\angle\boldsymbol{\mathrm{PSR}}\:=\:\mathrm{180}°\:−\:\mathrm{112}°\:=\:\mathrm{68}° \\ $$$$\mathrm{now},\:\boldsymbol{\mathrm{outter}}\angle\boldsymbol{\mathrm{PTR}}\:=\:\mathrm{2}×\mathrm{68}°\:=\:\mathrm{136}° \\ $$$$\mathrm{In}\:\boldsymbol{\mathrm{PQRT}}\:\boldsymbol{\mathrm{quadrilateral}}, \\ $$$$\angle\boldsymbol{\mathrm{PQR}}\:+\:\angle\boldsymbol{\mathrm{QRT}}\:+\:\angle\boldsymbol{\mathrm{PTR}}\:+\:\angle\boldsymbol{{x}}\:=\:\mathrm{360}° \\ $$$$\:\mathrm{112}\:+\:\mathrm{28}\:+\:\mathrm{136}\:+\:\boldsymbol{{x}}\:=\:\mathrm{360} \\ $$$$\:\:\boldsymbol{{x}}\:=\:\mathrm{84}°\:\left(\mathrm{this}\:\mathrm{is}\:\mathrm{your}\:\mathrm{answer}\right) \\ $$$$\:\: \\ $$
