Question Number 98067 by 995563401 last updated on 11/Jun/20

Answered by Farruxjano last updated on 11/Jun/20

Answered by 1549442205 last updated on 12/Jun/20
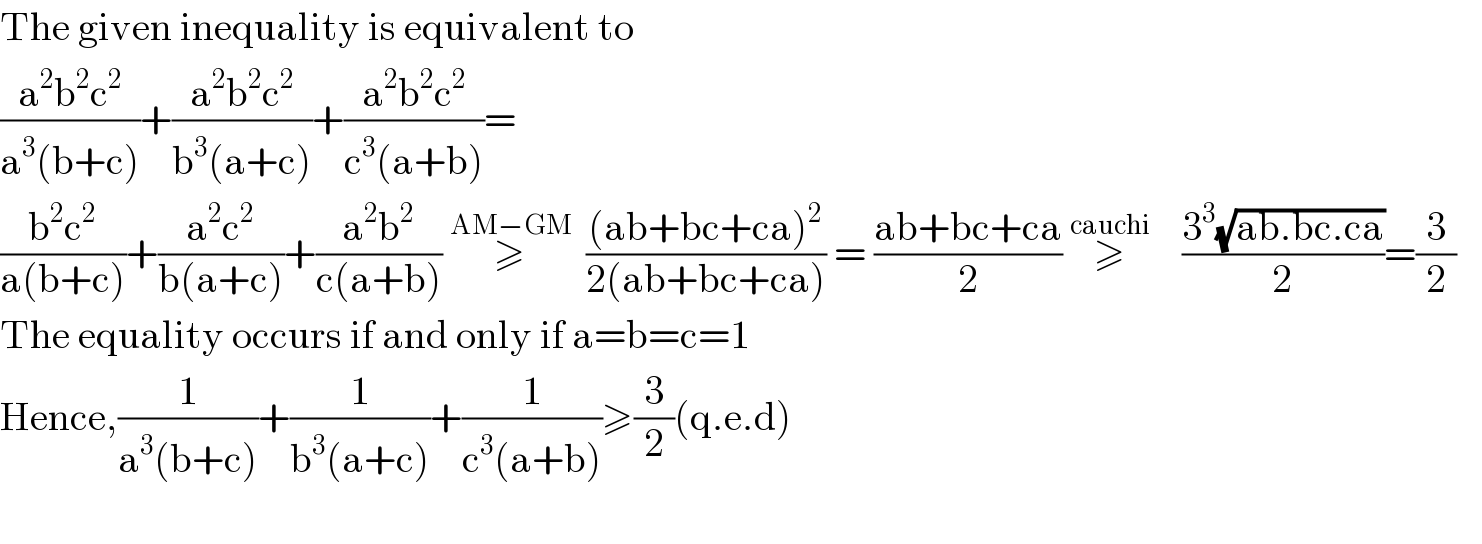
$$\mathrm{The}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{equivalent}\:\mathrm{to} \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} \left(\mathrm{b}+\mathrm{c}\right)}+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{3}} \left(\mathrm{a}+\mathrm{c}\right)}+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{c}^{\mathrm{3}} \left(\mathrm{a}+\mathrm{b}\right)}= \\ $$$$\frac{\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{a}\left(\mathrm{b}+\mathrm{c}\right)}+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{b}\left(\mathrm{a}+\mathrm{c}\right)}+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }{\mathrm{c}\left(\mathrm{a}+\mathrm{b}\right)}\:\overset{\mathrm{AM}−\mathrm{GM}} {\:\:\geqslant\:\:}\:\:\frac{\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)}\:=\:\frac{\mathrm{ab}+\mathrm{bc}+\mathrm{ca}}{\mathrm{2}}\:\overset{\mathrm{cauchi}} {\geqslant}\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{3}} \sqrt{\mathrm{ab}.\mathrm{bc}.\mathrm{ca}}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{occurs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{1} \\ $$$$\mathrm{Hence},\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} \left(\mathrm{b}+\mathrm{c}\right)}+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{3}} \left(\mathrm{a}+\mathrm{c}\right)}+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{3}} \left(\mathrm{a}+\mathrm{b}\right)}\geqslant\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$ \\ $$
