Question Number 98137 by Algoritm last updated on 11/Jun/20

Answered by Farruxjano last updated on 11/Jun/20
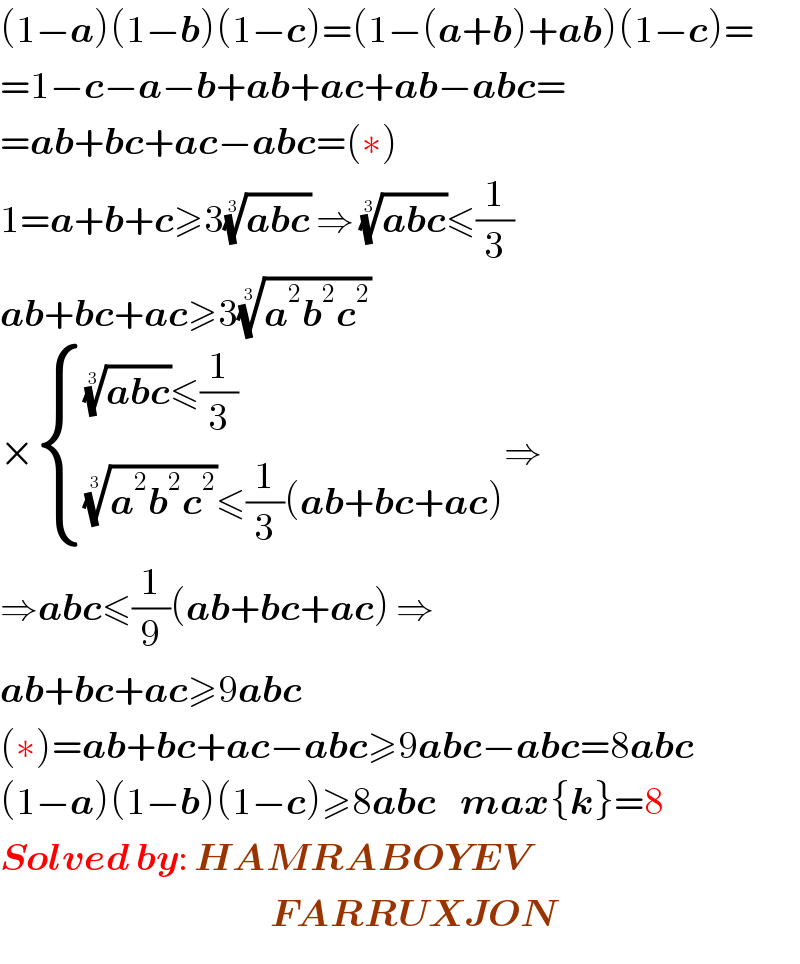
$$\left(\mathrm{1}−\boldsymbol{{a}}\right)\left(\mathrm{1}−\boldsymbol{{b}}\right)\left(\mathrm{1}−\boldsymbol{{c}}\right)=\left(\mathrm{1}−\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)+\boldsymbol{{ab}}\right)\left(\mathrm{1}−\boldsymbol{{c}}\right)= \\ $$$$=\mathrm{1}−\boldsymbol{{c}}−\boldsymbol{{a}}−\boldsymbol{{b}}+\boldsymbol{{ab}}+\boldsymbol{{ac}}+\boldsymbol{{ab}}−\boldsymbol{{abc}}= \\ $$$$=\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}−\boldsymbol{{abc}}=\left(\ast\right) \\ $$$$\mathrm{1}=\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\boldsymbol{{abc}}}\:\Rightarrow\:\sqrt[{\mathrm{3}}]{\boldsymbol{{abc}}}\leqslant\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} } \\ $$$$×\begin{cases}{\sqrt[{\mathrm{3}}]{\boldsymbol{{abc}}}\leqslant\frac{\mathrm{1}}{\mathrm{3}}}\\{\sqrt[{\mathrm{3}}]{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{3}}\left(\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}\right)}\end{cases}\Rightarrow \\ $$$$\Rightarrow\boldsymbol{{abc}}\leqslant\frac{\mathrm{1}}{\mathrm{9}}\left(\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}\right)\:\Rightarrow \\ $$$$\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}\geqslant\mathrm{9}\boldsymbol{{abc}} \\ $$$$\left(\ast\right)=\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ac}}−\boldsymbol{{abc}}\geqslant\mathrm{9}\boldsymbol{{abc}}−\boldsymbol{{abc}}=\mathrm{8}\boldsymbol{{abc}} \\ $$$$\left(\mathrm{1}−\boldsymbol{{a}}\right)\left(\mathrm{1}−\boldsymbol{{b}}\right)\left(\mathrm{1}−\boldsymbol{{c}}\right)\geqslant\mathrm{8}\boldsymbol{{abc}}\:\:\:\:\boldsymbol{{max}}\left\{\boldsymbol{{k}}\right\}=\mathrm{8} \\ $$$$\boldsymbol{{Solved}}\:\boldsymbol{{by}}:\:\boldsymbol{{HAMRABOYEV}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{FARRUXJON}} \\ $$
Commented by Farruxjano last updated on 11/Jun/20

$$\boldsymbol{{Is}}\:\boldsymbol{{it}}\:\boldsymbol{{right}},\:\boldsymbol{{please}}\:\boldsymbol{{check}}… \\ $$
Commented by Algoritm last updated on 11/Jun/20

$$\mathrm{thanks} \\ $$
Answered by MJS last updated on 11/Jun/20
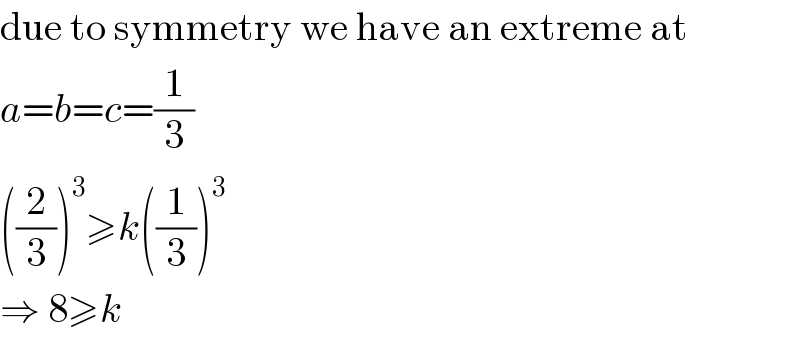
$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{we}\:\mathrm{have}\:\mathrm{an}\:\mathrm{extreme}\:\mathrm{at} \\ $$$${a}={b}={c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} \geqslant{k}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{8}\geqslant{k} \\ $$
Answered by mathmax by abdo last updated on 11/Jun/20
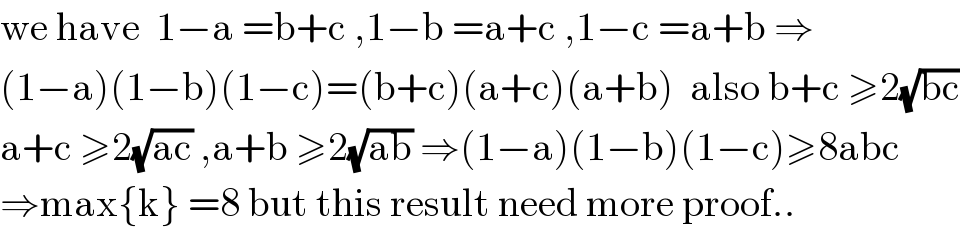
$$\mathrm{we}\:\mathrm{have}\:\:\mathrm{1}−\mathrm{a}\:=\mathrm{b}+\mathrm{c}\:,\mathrm{1}−\mathrm{b}\:=\mathrm{a}+\mathrm{c}\:,\mathrm{1}−\mathrm{c}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{a}\right)\left(\mathrm{1}−\mathrm{b}\right)\left(\mathrm{1}−\mathrm{c}\right)=\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}\right)\:\:\mathrm{also}\:\mathrm{b}+\mathrm{c}\:\geqslant\mathrm{2}\sqrt{\mathrm{bc}} \\ $$$$\mathrm{a}+\mathrm{c}\:\geqslant\mathrm{2}\sqrt{\mathrm{ac}}\:,\mathrm{a}+\mathrm{b}\:\geqslant\mathrm{2}\sqrt{\mathrm{ab}}\:\Rightarrow\left(\mathrm{1}−\mathrm{a}\right)\left(\mathrm{1}−\mathrm{b}\right)\left(\mathrm{1}−\mathrm{c}\right)\geqslant\mathrm{8abc}\: \\ $$$$\Rightarrow\mathrm{max}\left\{\mathrm{k}\right\}\:=\mathrm{8}\:\mathrm{but}\:\mathrm{this}\:\mathrm{result}\:\mathrm{need}\:\mathrm{more}\:\mathrm{proof}.. \\ $$
