Question Number 98149 by me2love2math last updated on 11/Jun/20

Commented by me2love2math last updated on 11/Jun/20

$${Q}\mathrm{1}\:{and}\:\mathrm{2}\:{pls} \\ $$
Answered by mr W last updated on 11/Jun/20

Commented by mr W last updated on 11/Jun/20
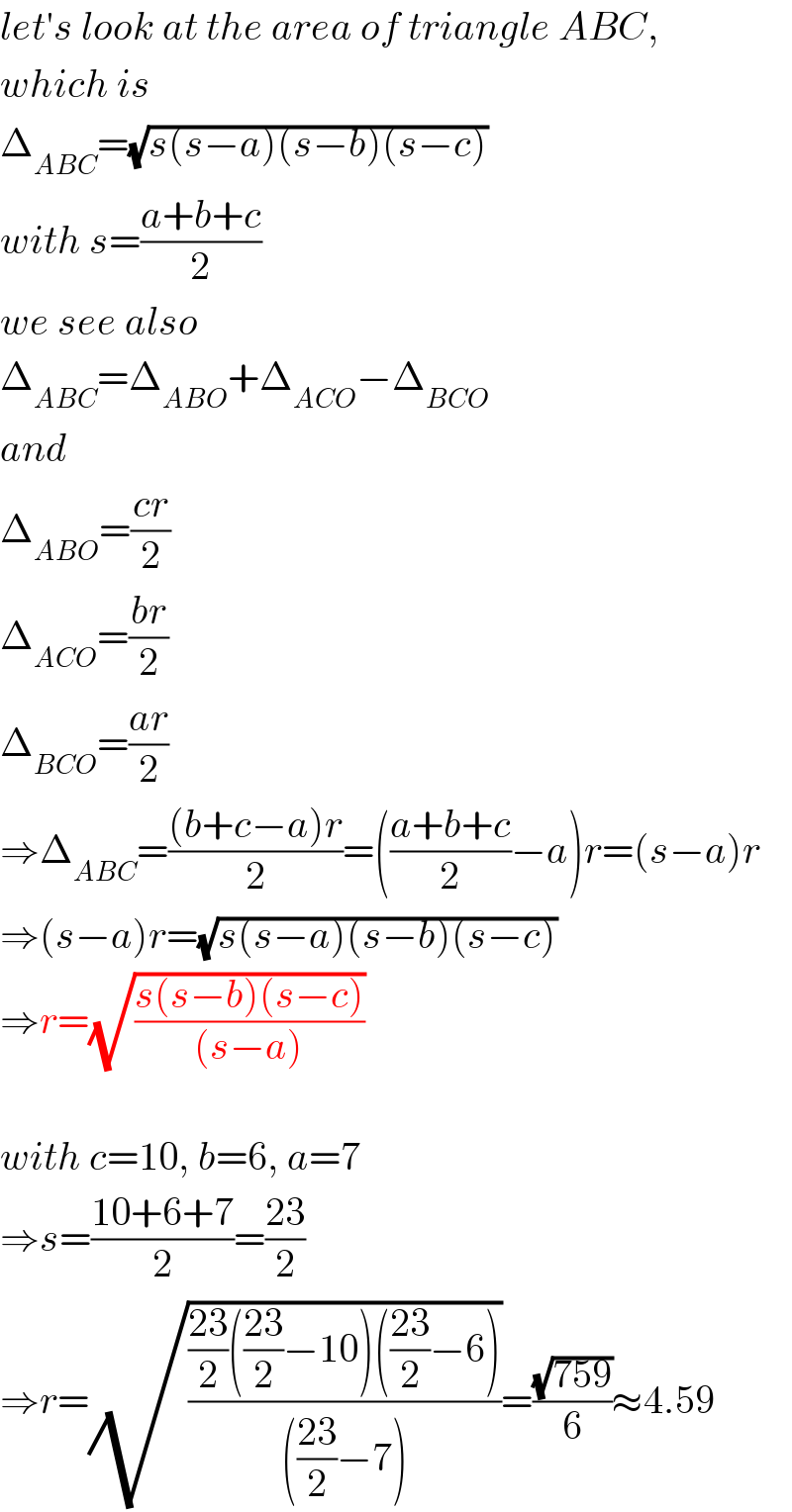
$${let}'{s}\:{look}\:{at}\:{the}\:{area}\:{of}\:{triangle}\:{ABC}, \\ $$$${which}\:{is} \\ $$$$\Delta_{{ABC}} =\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$${we}\:{see}\:{also} \\ $$$$\Delta_{{ABC}} =\Delta_{{ABO}} +\Delta_{{ACO}} −\Delta_{{BCO}} \\ $$$${and} \\ $$$$\Delta_{{ABO}} =\frac{{cr}}{\mathrm{2}} \\ $$$$\Delta_{{ACO}} =\frac{{br}}{\mathrm{2}} \\ $$$$\Delta_{{BCO}} =\frac{{ar}}{\mathrm{2}} \\ $$$$\Rightarrow\Delta_{{ABC}} =\frac{\left({b}+{c}−{a}\right){r}}{\mathrm{2}}=\left(\frac{{a}+{b}+{c}}{\mathrm{2}}−{a}\right){r}=\left({s}−{a}\right){r} \\ $$$$\Rightarrow\left({s}−{a}\right){r}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\Rightarrow{r}=\sqrt{\frac{{s}\left({s}−{b}\right)\left({s}−{c}\right)}{\left({s}−{a}\right)}} \\ $$$$ \\ $$$${with}\:{c}=\mathrm{10},\:{b}=\mathrm{6},\:{a}=\mathrm{7} \\ $$$$\Rightarrow{s}=\frac{\mathrm{10}+\mathrm{6}+\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\sqrt{\frac{\frac{\mathrm{23}}{\mathrm{2}}\left(\frac{\mathrm{23}}{\mathrm{2}}−\mathrm{10}\right)\left(\frac{\mathrm{23}}{\mathrm{2}}−\mathrm{6}\right)}{\left(\frac{\mathrm{23}}{\mathrm{2}}−\mathrm{7}\right)}}=\frac{\sqrt{\mathrm{759}}}{\mathrm{6}}\approx\mathrm{4}.\mathrm{59} \\ $$
Commented by me2love2math last updated on 12/Jun/20

$${many}\:{thx} \\ $$
