Question Number 98192 by behi83417@gmail.com last updated on 12/Jun/20
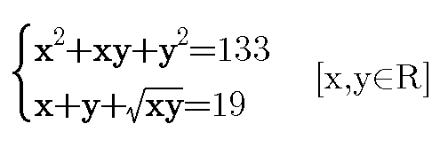
Commented by bemath last updated on 12/Jun/20
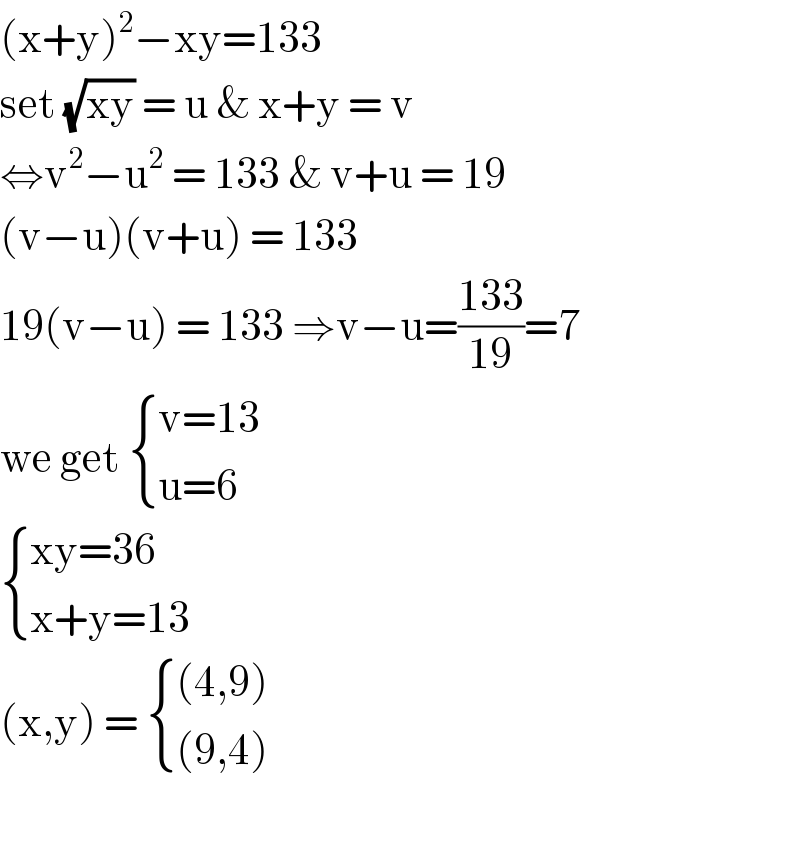
$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{xy}=\mathrm{133}\: \\ $$$$\mathrm{set}\:\sqrt{\mathrm{xy}}\:=\:\mathrm{u}\:\&\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{v} \\ $$$$\Leftrightarrow\mathrm{v}^{\mathrm{2}} −\mathrm{u}^{\mathrm{2}} \:=\:\mathrm{133}\:\&\:\mathrm{v}+\mathrm{u}\:=\:\mathrm{19} \\ $$$$\left(\mathrm{v}−\mathrm{u}\right)\left(\mathrm{v}+\mathrm{u}\right)\:=\:\mathrm{133} \\ $$$$\mathrm{19}\left(\mathrm{v}−\mathrm{u}\right)\:=\:\mathrm{133}\:\Rightarrow\mathrm{v}−\mathrm{u}=\frac{\mathrm{133}}{\mathrm{19}}=\mathrm{7} \\ $$$$\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{v}=\mathrm{13}}\\{\mathrm{u}=\mathrm{6}}\end{cases} \\ $$$$\begin{cases}{\mathrm{xy}=\mathrm{36}}\\{\mathrm{x}+\mathrm{y}=\mathrm{13}}\end{cases} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)\:=\:\begin{cases}{\left(\mathrm{4},\mathrm{9}\right)}\\{\left(\mathrm{9},\mathrm{4}\right)\:}\end{cases} \\ $$$$ \\ $$
Answered by mr W last updated on 12/Jun/20
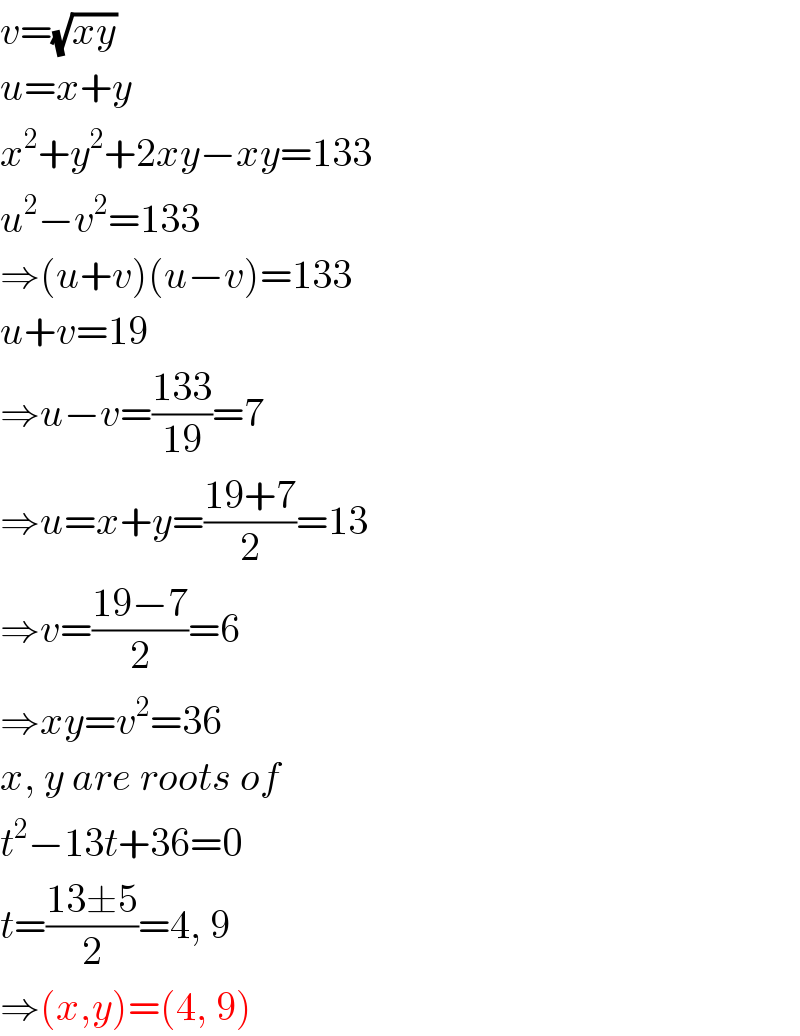
$${v}=\sqrt{{xy}} \\ $$$${u}={x}+{y} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}−{xy}=\mathrm{133} \\ $$$${u}^{\mathrm{2}} −{v}^{\mathrm{2}} =\mathrm{133} \\ $$$$\Rightarrow\left({u}+{v}\right)\left({u}−{v}\right)=\mathrm{133} \\ $$$${u}+{v}=\mathrm{19} \\ $$$$\Rightarrow{u}−{v}=\frac{\mathrm{133}}{\mathrm{19}}=\mathrm{7} \\ $$$$\Rightarrow{u}={x}+{y}=\frac{\mathrm{19}+\mathrm{7}}{\mathrm{2}}=\mathrm{13} \\ $$$$\Rightarrow{v}=\frac{\mathrm{19}−\mathrm{7}}{\mathrm{2}}=\mathrm{6} \\ $$$$\Rightarrow{xy}={v}^{\mathrm{2}} =\mathrm{36} \\ $$$${x},\:{y}\:{are}\:{roots}\:{of} \\ $$$${t}^{\mathrm{2}} −\mathrm{13}{t}+\mathrm{36}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{13}\pm\mathrm{5}}{\mathrm{2}}=\mathrm{4},\:\mathrm{9} \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\mathrm{4},\:\mathrm{9}\right) \\ $$
Answered by MJS last updated on 12/Jun/20
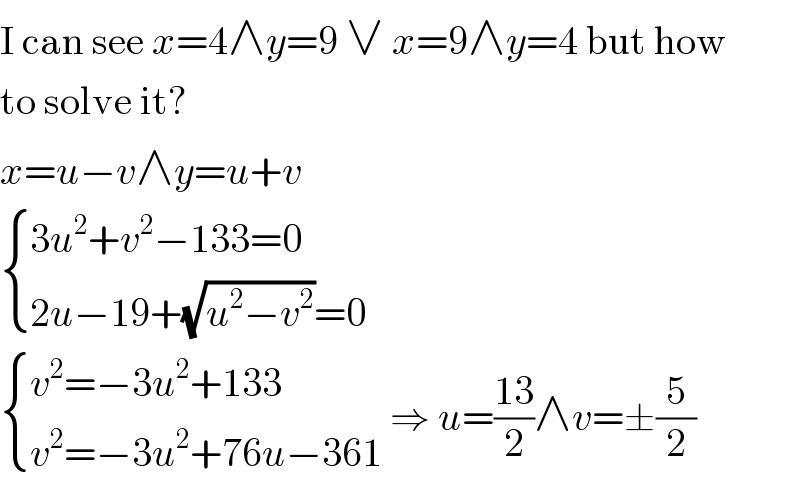
$$\mathrm{I}\:\mathrm{can}\:\mathrm{see}\:{x}=\mathrm{4}\wedge{y}=\mathrm{9}\:\vee\:{x}=\mathrm{9}\wedge{y}=\mathrm{4}\:\mathrm{but}\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{it}? \\ $$$${x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\begin{cases}{\mathrm{3}{u}^{\mathrm{2}} +{v}^{\mathrm{2}} −\mathrm{133}=\mathrm{0}}\\{\mathrm{2}{u}−\mathrm{19}+\sqrt{{u}^{\mathrm{2}} −{v}^{\mathrm{2}} }=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{{v}^{\mathrm{2}} =−\mathrm{3}{u}^{\mathrm{2}} +\mathrm{133}}\\{{v}^{\mathrm{2}} =−\mathrm{3}{u}^{\mathrm{2}} +\mathrm{76}{u}−\mathrm{361}}\end{cases}\:\Rightarrow\:{u}=\frac{\mathrm{13}}{\mathrm{2}}\wedge{v}=\pm\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 12/Jun/20

$$\mathrm{thanks}\:\mathrm{to}\:\mathrm{all}\:\mathrm{my}\:\mathrm{masters}. \\ $$
