Question Number 98213 by me2love2math last updated on 12/Jun/20

Commented by bemath last updated on 12/Jun/20
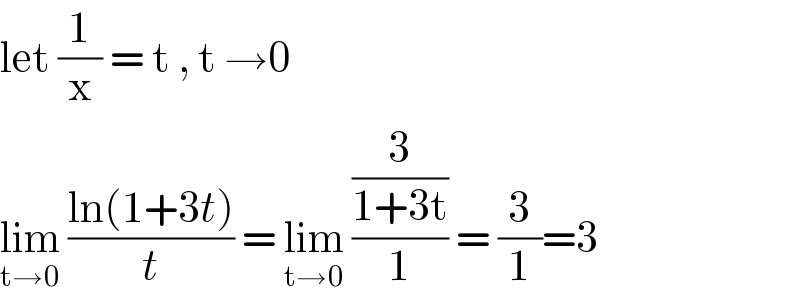
$$\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{t}\:,\:\mathrm{t}\:\rightarrow\mathrm{0}\: \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{3}{t}\right)}{{t}}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{3}}{\mathrm{1}+\mathrm{3t}}}{\mathrm{1}}\:=\:\frac{\mathrm{3}}{\mathrm{1}}=\mathrm{3} \\ $$
Answered by Rio Michael last updated on 12/Jun/20
![lim_(x→∞) [x ln(1 + (3/x))] = lim_(x→∞) [x ln(((x +3)/x))] By l′hopitals rule lim_(x→∞) ((2x−3)/(3 + x)) + lim_(x→) xln(1 + (3/x)) = 3+ 0 = 3 ⇒ lim_(x→∞) [x ln(1 + (3/x))] = 3](https://www.tinkutara.com/question/Q98222.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[{x}\:\mathrm{ln}\left(\mathrm{1}\:+\:\frac{\mathrm{3}}{{x}}\right)\right]\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[{x}\:\mathrm{ln}\left(\frac{{x}\:+\mathrm{3}}{{x}}\right)\right]\: \\ $$$$\mathrm{By}\:\mathrm{l}'\mathrm{hopitals}\:\mathrm{rule}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{3}\:+\:{x}}\:+\:\underset{{x}\rightarrow} {\mathrm{lim}}\:{x}\mathrm{ln}\left(\mathrm{1}\:+\:\frac{\mathrm{3}}{{x}}\right)\:=\:\mathrm{3}+\:\mathrm{0}\:=\:\mathrm{3} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[{x}\:\mathrm{ln}\left(\mathrm{1}\:+\:\frac{\mathrm{3}}{{x}}\right)\right]\:=\:\mathrm{3} \\ $$$$\: \\ $$
Answered by MJS last updated on 12/Jun/20
![lim_(x→+∞) (xln (1+(3/x))) =^([x=(1/t)]) lim_(t→0^+ ) ((ln (3t+1))/t) = =lim_(t→0^+ ) (((d/dt)[ln (3t+1)])/((d/dt)[t])) =lim_(t→0^+ ) (3/(3t+1)) =3](https://www.tinkutara.com/question/Q98223.png)
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left({x}\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{3}}{{x}}\right)\right)\:\overset{\left[{x}=\frac{\mathrm{1}}{{t}}\right]} {=}\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{3}{t}+\mathrm{1}\right)}{{t}}\:= \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\frac{{d}}{{dt}}\left[\mathrm{ln}\:\left(\mathrm{3}{t}+\mathrm{1}\right)\right]}{\frac{{d}}{{dt}}\left[{t}\right]}\:=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{3}}{\mathrm{3}{t}+\mathrm{1}}\:=\mathrm{3} \\ $$
