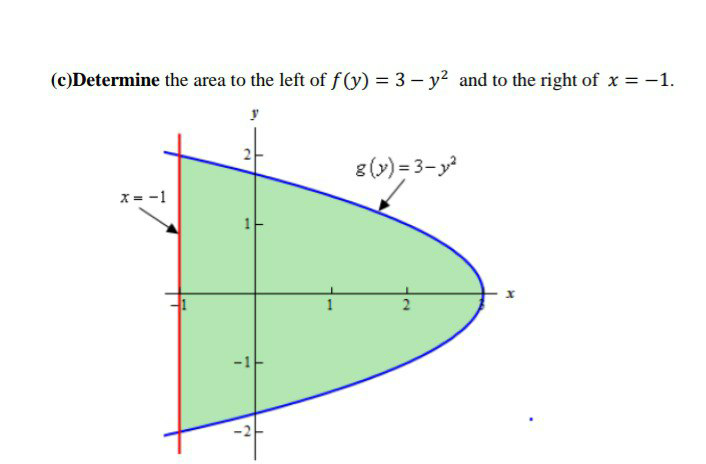
Question Number 98214 by me2love2math last updated on 12/Jun/20
Commented by mr W last updated on 12/Jun/20

$${A}=\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{4}×\mathrm{4}=\frac{\mathrm{32}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 12/Jun/20
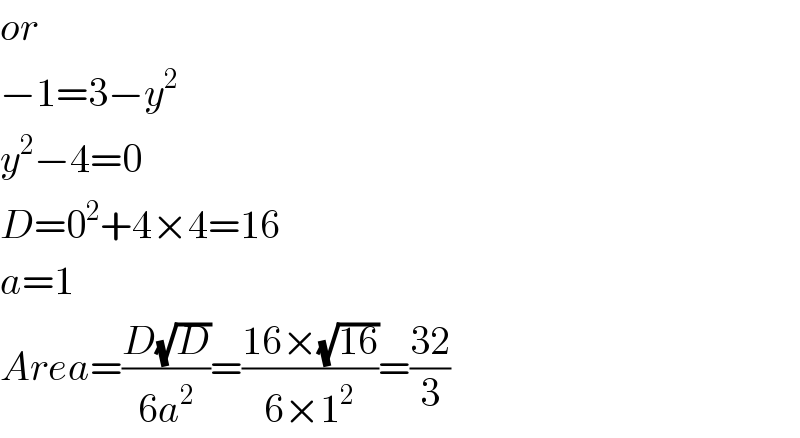
$${or} \\ $$$$−\mathrm{1}=\mathrm{3}−{y}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$${D}=\mathrm{0}^{\mathrm{2}} +\mathrm{4}×\mathrm{4}=\mathrm{16} \\ $$$${a}=\mathrm{1} \\ $$$${Area}=\frac{{D}\sqrt{{D}}}{\mathrm{6}{a}^{\mathrm{2}} }=\frac{\mathrm{16}×\sqrt{\mathrm{16}}}{\mathrm{6}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{32}}{\mathrm{3}} \\ $$
Answered by Rio Michael last updated on 12/Jun/20
![to get the limits lets solve x = 3−y^2 and x = −1 ⇒ −1 = 3−y^2 ⇔ y = ± 2. the required area A = ∫_(−2) ^2 (right function)−(left function) ⇒ A = ∫_(−2) ^2 (3−y^2 −(−1)dy = ∫_(−2) ^2 (4 −y^2 )dy = [4y−(y^3 /3)]_(−2) ^2 = (8−(8/3))−(−8 + (8/3)) = 16 square units. Recall for this type of problems take the integral of the right function − the left function.](https://www.tinkutara.com/question/Q98219.png)
$$\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{lets}\:\mathrm{solve}\:{x}\:=\:\mathrm{3}−{y}^{\mathrm{2}} \:\mathrm{and}\:{x}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:−\mathrm{1}\:=\:\mathrm{3}−{y}^{\mathrm{2}} \:\Leftrightarrow\:{y}\:=\:\pm\:\mathrm{2}. \\ $$$$\mathrm{the}\:\mathrm{required}\:\mathrm{area}\:{A}\:=\:\int_{−\mathrm{2}} ^{\mathrm{2}} \:\left(\mathrm{right}\:\mathrm{function}\right)−\left(\mathrm{left}\:\mathrm{function}\right) \\ $$$$\Rightarrow\:{A}\:=\:\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{3}−{y}^{\mathrm{2}} −\left(−\mathrm{1}\right){dy}\:=\:\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{4}\:−{y}^{\mathrm{2}} \right){dy}\:=\:\left[\mathrm{4}{y}−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}\right]_{−\mathrm{2}} ^{\mathrm{2}} \right. \\ $$$$=\:\left(\mathrm{8}−\frac{\mathrm{8}}{\mathrm{3}}\right)−\left(−\mathrm{8}\:+\:\frac{\mathrm{8}}{\mathrm{3}}\right)\:=\:\mathrm{16}\:\mathrm{square}\:\mathrm{units}. \\ $$$$\mathcal{R}\mathrm{ecall}\:\mathrm{for}\:\mathrm{this}\:\mathrm{type}\:\mathrm{of}\:\mathrm{problems}\:\mathrm{take}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{of}\:\mathrm{the}\:\mathrm{right}\:\mathrm{function} \\ $$$$−\:\mathrm{the}\:\mathrm{left}\:\mathrm{function}. \\ $$$$ \\ $$
Answered by MJS last updated on 12/Jun/20
![x=3−y^2 ⇔ y=±(√(3−x)) 2∫_(−1) ^3 (√(3−x))dx=−(4/3)[(3−x)^(3/2) ]_(−1) ^3 =((32)/3)](https://www.tinkutara.com/question/Q98221.png)
$${x}=\mathrm{3}−{y}^{\mathrm{2}} \:\Leftrightarrow\:{y}=\pm\sqrt{\mathrm{3}−{x}} \\ $$$$\mathrm{2}\underset{−\mathrm{1}} {\overset{\mathrm{3}} {\int}}\sqrt{\mathrm{3}−{x}}{dx}=−\frac{\mathrm{4}}{\mathrm{3}}\left[\left(\mathrm{3}−{x}\right)^{\mathrm{3}/\mathrm{2}} \right]_{−\mathrm{1}} ^{\mathrm{3}} =\frac{\mathrm{32}}{\mathrm{3}} \\ $$
