Question-98259

Question Number 98259 by Hassen_Timol last updated on 12/Jun/20

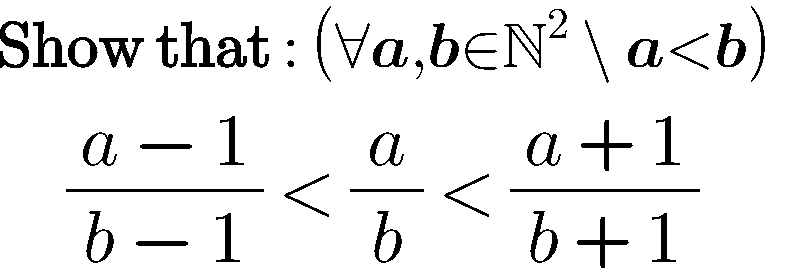
Commented by Hassen_Timol last updated on 12/Jun/20

$$\mathrm{Please} \\ $$

Commented by PRITHWISH SEN 2 last updated on 12/Jun/20

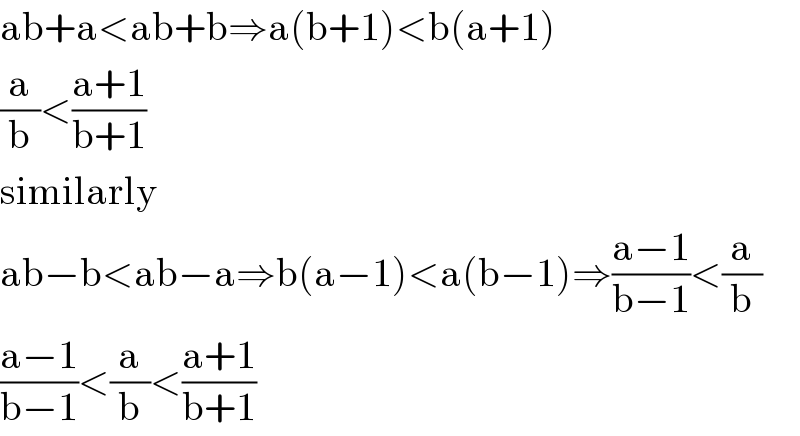
ab+a<ab+b⇒a(b+1)<b(a+1) (a/b)<((a+1)/(b+1)) similarly ab−b<ab−a⇒b(a−1)<a(b−1)⇒((a−1)/(b−1))<(a/b) ((a−1)/(b−1))<(a/b)<((a+1)/(b+1))

$$\mathrm{ab}+\mathrm{a}<\mathrm{ab}+\mathrm{b}\Rightarrow\mathrm{a}\left(\mathrm{b}+\mathrm{1}\right)<\mathrm{b}\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}} \\ $$$$\mathrm{similarly} \\ $$$$\mathrm{ab}−\mathrm{b}<\mathrm{ab}−\mathrm{a}\Rightarrow\mathrm{b}\left(\mathrm{a}−\mathrm{1}\right)<\mathrm{a}\left(\mathrm{b}−\mathrm{1}\right)\Rightarrow\frac{\mathrm{a}−\mathrm{1}}{\mathrm{b}−\mathrm{1}}<\frac{\mathrm{a}}{\mathrm{b}} \\ $$$$\frac{\mathrm{a}−\mathrm{1}}{\mathrm{b}−\mathrm{1}}<\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}} \\ $$

Commented by Hassen_Timol last updated on 12/Jun/20

$$\left.\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{much}}\:\::-\right) \\ $$

Commented by PRITHWISH SEN 2 last updated on 12/Jun/20

$$\mathrm{welcome} \\ $$

Answered by mr W last updated on 12/Jun/20

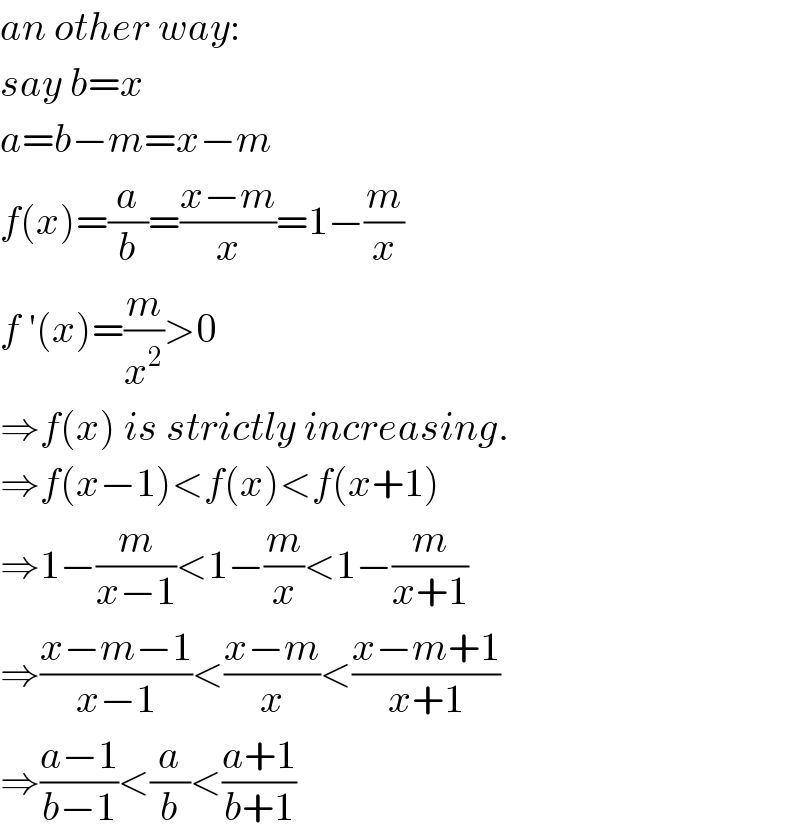
an other way: say b=x a=b−m=x−m f(x)=(a/b)=((x−m)/x)=1−(m/x) f ′(x)=(m/x^2 )>0 ⇒f(x) is strictly increasing. ⇒f(x−1)<f(x)<f(x+1) ⇒1−(m/(x−1))<1−(m/x)<1−(m/(x+1)) ⇒((x−m−1)/(x−1))<((x−m)/x)<((x−m+1)/(x+1)) ⇒((a−1)/(b−1))<(a/b)<((a+1)/(b+1))

$${an}\:{other}\:{way}: \\ $$$${say}\:{b}={x} \\ $$$${a}={b}−{m}={x}−{m} \\ $$$${f}\left({x}\right)=\frac{{a}}{{b}}=\frac{{x}−{m}}{{x}}=\mathrm{1}−\frac{{m}}{{x}} \\ $$$${f}\:'\left({x}\right)=\frac{{m}}{{x}^{\mathrm{2}} }>\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{strictly}\:{increasing}. \\ $$$$\Rightarrow{f}\left({x}−\mathrm{1}\right)<{f}\left({x}\right)<{f}\left({x}+\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{1}−\frac{{m}}{{x}−\mathrm{1}}<\mathrm{1}−\frac{{m}}{{x}}<\mathrm{1}−\frac{{m}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{x}−{m}−\mathrm{1}}{{x}−\mathrm{1}}<\frac{{x}−{m}}{{x}}<\frac{{x}−{m}+\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{a}−\mathrm{1}}{{b}−\mathrm{1}}<\frac{{a}}{{b}}<\frac{{a}+\mathrm{1}}{{b}+\mathrm{1}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 12/Jun/20

$$\mathrm{wow}! \\ $$

Answered by mathmax by abdo last updated on 12/Jun/20

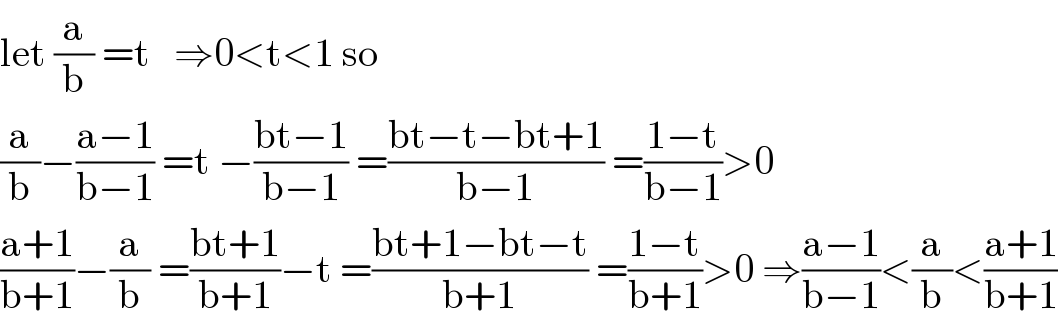
let (a/b) =t ⇒0<t<1 so (a/b)−((a−1)/(b−1)) =t −((bt−1)/(b−1)) =((bt−t−bt+1)/(b−1)) =((1−t)/(b−1))>0 ((a+1)/(b+1))−(a/b) =((bt+1)/(b+1))−t =((bt+1−bt−t)/(b+1)) =((1−t)/(b+1))>0 ⇒((a−1)/(b−1))<(a/b)<((a+1)/(b+1))

$$\mathrm{let}\:\frac{\mathrm{a}}{\mathrm{b}}\:=\mathrm{t}\:\:\:\Rightarrow\mathrm{0}<\mathrm{t}<\mathrm{1}\:\mathrm{so} \\ $$$$\frac{\mathrm{a}}{\mathrm{b}}−\frac{\mathrm{a}−\mathrm{1}}{\mathrm{b}−\mathrm{1}}\:=\mathrm{t}\:−\frac{\mathrm{bt}−\mathrm{1}}{\mathrm{b}−\mathrm{1}}\:=\frac{\mathrm{bt}−\mathrm{t}−\mathrm{bt}+\mathrm{1}}{\mathrm{b}−\mathrm{1}}\:=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{b}−\mathrm{1}}>\mathrm{0} \\ $$$$\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}}−\frac{\mathrm{a}}{\mathrm{b}}\:=\frac{\mathrm{bt}+\mathrm{1}}{\mathrm{b}+\mathrm{1}}−\mathrm{t}\:=\frac{\mathrm{bt}+\mathrm{1}−\mathrm{bt}−\mathrm{t}}{\mathrm{b}+\mathrm{1}}\:=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{b}+\mathrm{1}}>\mathrm{0}\:\Rightarrow\frac{\mathrm{a}−\mathrm{1}}{\mathrm{b}−\mathrm{1}}<\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 13/Jun/20

$$\mathrm{nice} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply