Question Number 98290 by Rio Michael last updated on 12/Jun/20
Commented by Rio Michael last updated on 13/Jun/20

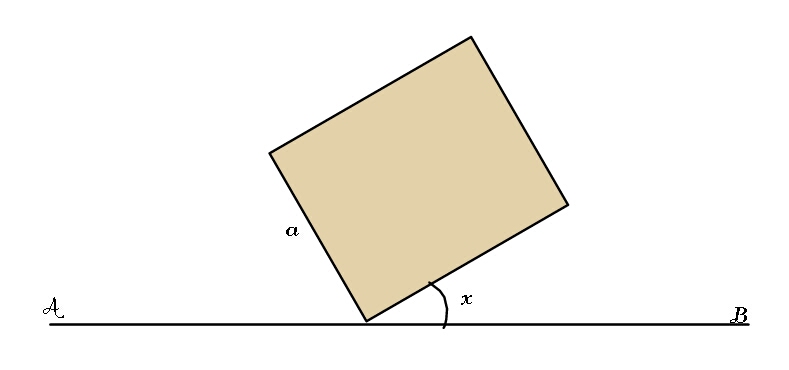
$$\mathrm{The}\:\mathrm{above}\:\mathrm{figure}\:\mathrm{shows}\:\mathrm{a}\:\mathrm{square}\:\mathrm{lamina}\:\mathrm{of}\:\mathrm{side}\:{a}\:\mathrm{with}\:\mathrm{vertex}\: \\ $$$$\mathrm{inclined}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:{x},\:\mathrm{0}\:\leqslant\:{x}\leqslant\:\frac{\pi}{\mathrm{2}},\:\mathrm{placed}\:\mathrm{on}\:\mathrm{a}\:\mathrm{line}\:{AB}. \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lamina}\:\mathrm{is}\:\mathrm{at}\:\mathrm{a}\:\mathrm{distance}\:\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{sin}\:\left({x}\:+\:\frac{\pi}{\mathrm{4}}\right)\:\mathrm{from} \\ $$$${AB}.\:\mathrm{The}\:\mathrm{lamina}\:\mathrm{is}\:\mathrm{rotated}\:\mathrm{completely}\:\mathrm{about}\:\mathrm{the}\:\mathrm{line}\:{AB}. \\ $$$$\mathrm{use}\:\mathrm{the}\:\mathrm{second}\:\mathrm{law}\:\mathrm{of}\:\mathrm{Pappus}\:\mathrm{or}\:\mathrm{otherwise}\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\mathrm{the}\:\mathrm{volume}\:\mathrm{generated}\:\mathrm{is}\:\sqrt{\mathrm{2}}\:\pi{a}^{\mathrm{3}} \:\mathrm{sin}\:\left({x}\:+\:\frac{\pi}{\mathrm{4}}\right). \\ $$
