Menu Close

Question-98293

Tinku Tara 0 Comments
Pin




Question Number 98293 by I want to learn more last updated on 12/Jun/20
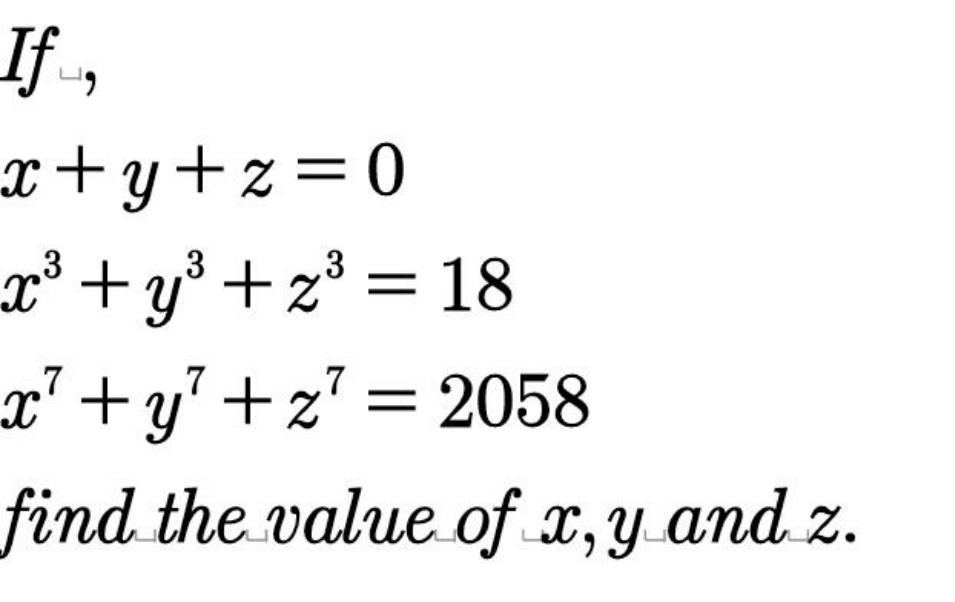
Answered by mr W last updated on 12/Jun/20
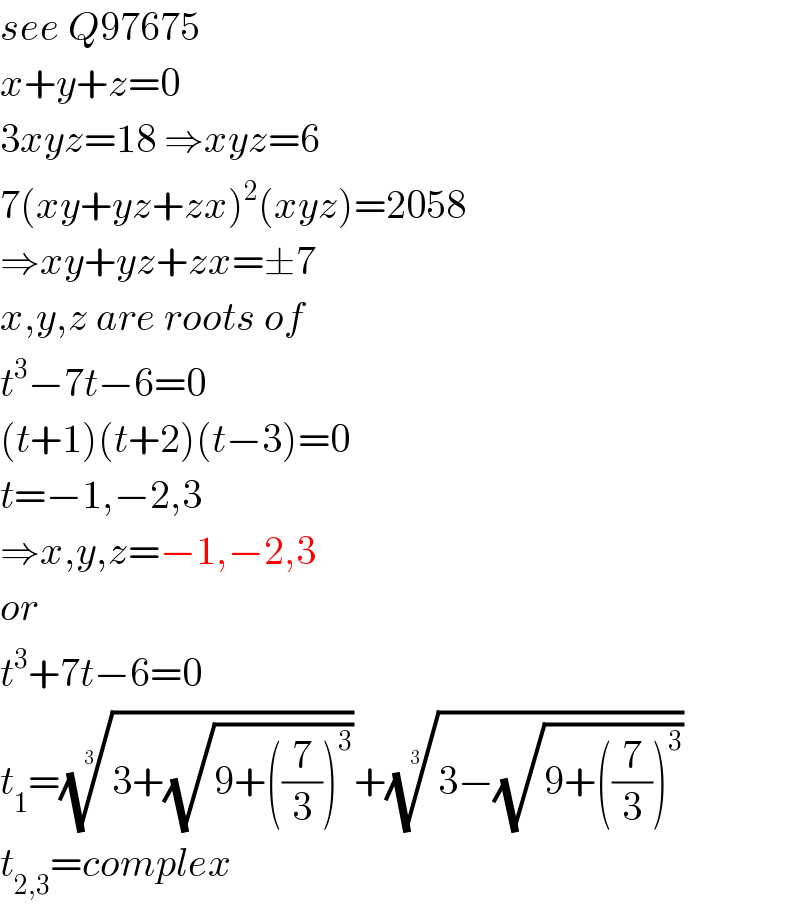
see Q97675 x+y+z=0 3xyz=18 ⇒xyz=6 7(xy+yz+zx)^2 (xyz)=2058 ⇒xy+yz+zx=±7 x,y,z are roots of t^3 −7t−6=0 (t+1)(t+2)(t−3)=0 t=−1,−2,3 ⇒x,y,z=−1,−2,3 or t^3 +7t−6=0 t_1 =((3+(√(9+((7/3))^3 ))))^(1/3) +((3−(√(9+((7/3))^3 ))))^(1/3) t_(2,3) =complex
$${see}\:{Q}\mathrm{97675} \\ $$$${x}+{y}+{z}=\mathrm{0} \\ $$$$\mathrm{3}{xyz}=\mathrm{18}\:\Rightarrow{xyz}=\mathrm{6} \\ $$$$\mathrm{7}\left({xy}+{yz}+{zx}\right)^{\mathrm{2}} \left({xyz}\right)=\mathrm{2058} \\ $$$$\Rightarrow{xy}+{yz}+{zx}=\pm\mathrm{7} \\ $$$${x},{y},{z}\:{are}\:{roots}\:{of} \\ $$$${t}^{\mathrm{3}} −\mathrm{7}{t}−\mathrm{6}=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)\left({t}−\mathrm{3}\right)=\mathrm{0} \\ $$$${t}=−\mathrm{1},−\mathrm{2},\mathrm{3} \\ $$$$\Rightarrow{x},{y},{z}=−\mathrm{1},−\mathrm{2},\mathrm{3} \\ $$$${or} \\ $$$${t}^{\mathrm{3}} +\mathrm{7}{t}−\mathrm{6}=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathrm{3}+\sqrt{\mathrm{9}+\left(\frac{\mathrm{7}}{\mathrm{3}}\right)^{\mathrm{3}} }}+\sqrt[{\mathrm{3}}]{\mathrm{3}−\sqrt{\mathrm{9}+\left(\frac{\mathrm{7}}{\mathrm{3}}\right)^{\mathrm{3}} }} \\ $$$${t}_{\mathrm{2},\mathrm{3}} ={complex} \\ $$
Commented by I want to learn more last updated on 12/Jun/20
wow, thanks sir.
$$\mathrm{wow},\:\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by 1549442205 last updated on 13/Jun/20
we have z=−(x+y).Replace into ii)we get x^3 +y^3 −(x+y)^3 =18⇔x^3 +y^3 −(x^3 +3xy(x+y)+y^3 )=18 ⇔−3xy(x+y)=18⇔3xyz=18⇔xyz=6 Replace into iii)we get x^7 +y^7 −(x+y)^7 =2058(∗) we have:x^3 +y^3 =(x+y)^3 −3xy(x+y)=−z^3 +3xyz=18−z^3 (1) x^5 +y^5 =(x+y)^5 −5xy(x^3 +y^3 )−10x^2 y^2 (x+y) =−z^5 +5xyz^3 −90xy+10x^2 y^2 z=−z^5 +30z^2 −30xy(2) (x+y)^7 =x^7 +y^7 +7xy(x^5 +y^5 )+21x^2 y^2 (x^3 +y^3 )+35x^3 y^3 (x+y) =x^7 +y^7 −42z^4 +1260z−210x^2 y^2 −756z+378x^2 y^2 −210x^2 y^2 (3). Replace into (∗)we get : 42z^4 +42x^2 y^2 −504z=2058⇔z^4 +x^2 y^2 −12z=49 z^4 +((36)/z^2 )−12z−49=0⇔z^6 −12z^3 −49z^2 +36=0 ⇔(z+1)(z+2)(z−3)(z^3 +7z−6)=0 ⇔z∈{−1;−2;3;((^3 (√(81+3(√(1758)))))/3)+((−7^3 (√2))/(^3 (√(162+6(√(1758))))))} a/for z∈{−1;−2;3} We get (x;y;z)={(−1;−2;3);(−1;3;−2);(−2;−1;3);(−2;3;−1) (3;−1;−2);(3;−2;−1)} b/for z=((^3 (√(81+3(√(1758)))))/3)+((−7^3 (√2))/(^3 (√(162+6(√(1758)))))) x,y are image roots
$$\left.\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{z}}=−\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right).\boldsymbol{\mathrm{Replace}}\:\boldsymbol{\mathrm{into}}\:\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} −\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{3}} =\mathrm{18}\Leftrightarrow\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} −\left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)+\boldsymbol{\mathrm{y}}^{\mathrm{3}} \right)=\mathrm{18} \\ $$$$\Leftrightarrow−\mathrm{3}\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)=\mathrm{18}\Leftrightarrow\mathrm{3}\boldsymbol{\mathrm{xyz}}=\mathrm{18}\Leftrightarrow\boldsymbol{\mathrm{xyz}}=\mathrm{6}\: \\ $$$$\left.\boldsymbol{\mathrm{Replace}}\:\boldsymbol{\mathrm{into}}\:\boldsymbol{\mathrm{iii}}\right)\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\boldsymbol{\mathrm{x}}^{\mathrm{7}} +\boldsymbol{\mathrm{y}}^{\mathrm{7}} −\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{7}} =\mathrm{2058}\left(\ast\right) \\ $$$$\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{have}}:\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} =\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{3}} −\mathrm{3}\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)=−\boldsymbol{\mathrm{z}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{\mathrm{xyz}}=\mathrm{18}−\boldsymbol{\mathrm{z}}^{\mathrm{3}} \left(\mathrm{1}\right) \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{5}} +\boldsymbol{\mathrm{y}}^{\mathrm{5}} =\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{5}} −\mathrm{5}\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} \right)−\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right) \\ $$$$=−\boldsymbol{\mathrm{z}}^{\mathrm{5}} +\mathrm{5}\boldsymbol{\mathrm{xyz}}^{\mathrm{3}} −\mathrm{90}\boldsymbol{\mathrm{xy}}+\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{z}}=−\boldsymbol{\mathrm{z}}^{\mathrm{5}} +\mathrm{30}\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\mathrm{30}\boldsymbol{\mathrm{xy}}\left(\mathrm{2}\right) \\ $$$$\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{7}} =\boldsymbol{\mathrm{x}}^{\mathrm{7}} +\boldsymbol{\mathrm{y}}^{\mathrm{7}} +\mathrm{7}\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{5}} +\boldsymbol{\mathrm{y}}^{\mathrm{5}} \right)+\mathrm{21}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} \right)+\mathrm{35}\boldsymbol{\mathrm{x}}^{\mathrm{3}} \boldsymbol{\mathrm{y}}^{\mathrm{3}} \left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right) \\ $$$$=\boldsymbol{\mathrm{x}}^{\mathrm{7}} +\boldsymbol{\mathrm{y}}^{\mathrm{7}} −\mathrm{42}\boldsymbol{\mathrm{z}}^{\mathrm{4}} +\mathrm{1260}\boldsymbol{\mathrm{z}}−\mathrm{210}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{756}\boldsymbol{\mathrm{z}}+\mathrm{378}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{210x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \left(\mathrm{3}\right). \\ $$$$\boldsymbol{\mathrm{Replace}}\:\boldsymbol{\mathrm{into}}\:\left(\ast\right)\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:: \\ $$$$\mathrm{42}\boldsymbol{\mathrm{z}}^{\mathrm{4}} +\mathrm{42}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{504}\boldsymbol{\mathrm{z}}=\mathrm{2058}\Leftrightarrow\boldsymbol{\mathrm{z}}^{\mathrm{4}} +\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{12}\boldsymbol{\mathrm{z}}=\mathrm{49} \\ $$$$\boldsymbol{\mathrm{z}}^{\mathrm{4}} +\frac{\mathrm{36}}{\boldsymbol{\mathrm{z}}^{\mathrm{2}} }−\mathrm{12}\boldsymbol{\mathrm{z}}−\mathrm{49}=\mathrm{0}\Leftrightarrow\boldsymbol{\mathrm{z}}^{\mathrm{6}} −\mathrm{12}\boldsymbol{\mathrm{z}}^{\mathrm{3}} −\mathrm{49}\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\mathrm{36}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\boldsymbol{\mathrm{z}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{z}}+\mathrm{2}\right)\left(\boldsymbol{\mathrm{z}}−\mathrm{3}\right)\left(\mathrm{z}^{\mathrm{3}} +\mathrm{7z}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\boldsymbol{\mathrm{z}}\in\left\{−\mathrm{1};−\mathrm{2};\mathrm{3};\frac{\:^{\mathrm{3}} \sqrt{\mathrm{81}+\mathrm{3}\sqrt{\mathrm{1758}}}}{\mathrm{3}}+\frac{−\mathrm{7}\:^{\mathrm{3}} \sqrt{\mathrm{2}}}{\:^{\mathrm{3}} \sqrt{\mathrm{162}+\mathrm{6}\sqrt{\mathrm{1758}}}}\right\} \\ $$$$\mathrm{a}/\mathrm{for}\:\mathrm{z}\in\left\{−\mathrm{1};−\mathrm{2};\mathrm{3}\right\} \\ $$$$\mathrm{We}\:\mathrm{get}\:\left(\mathrm{x};\mathrm{y};\mathrm{z}\right)=\left\{\left(−\mathrm{1};−\mathrm{2};\mathrm{3}\right);\left(−\mathrm{1};\mathrm{3};−\mathrm{2}\right);\left(−\mathrm{2};−\mathrm{1};\mathrm{3}\right);\left(−\mathrm{2};\mathrm{3};−\mathrm{1}\right)\right. \\ $$$$\left.\left(\mathrm{3};−\mathrm{1};−\mathrm{2}\right);\left(\mathrm{3};−\mathrm{2};−\mathrm{1}\right)\right\} \\ $$$$\mathrm{b}/\mathrm{for}\:\mathrm{z}=\frac{\:^{\mathrm{3}} \sqrt{\mathrm{81}+\mathrm{3}\sqrt{\mathrm{1758}}}}{\mathrm{3}}+\frac{−\mathrm{7}\:^{\mathrm{3}} \sqrt{\mathrm{2}}}{\:^{\mathrm{3}} \sqrt{\mathrm{162}+\mathrm{6}\sqrt{\mathrm{1758}}}} \\ $$$$\mathrm{x},\mathrm{y}\:\mathrm{are}\:\mathrm{image}\:\mathrm{roots} \\ $$$$ \\ $$
Commented by I want to learn more last updated on 13/Jun/20
Wow, thanks sir
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *