Question Number 98306 by me2love2math last updated on 12/Jun/20

Commented by me2love2math last updated on 12/Jun/20
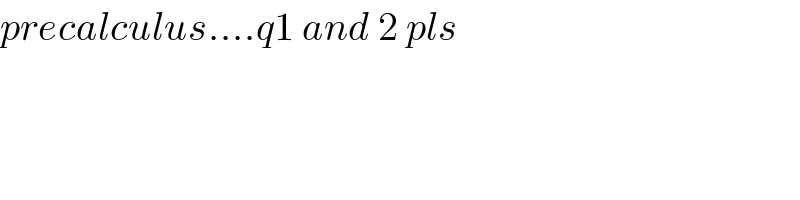
$${precalculus}….{q}\mathrm{1}\:{and}\:\mathrm{2}\:{pls} \\ $$
Answered by Rio Michael last updated on 12/Jun/20

$${f}\left({t}\right)\:=\:−\mathrm{0}.\mathrm{005}\left({t}−\mathrm{12}\right)\left({t}+\mathrm{3}\right)\left({t}+\mathrm{0}.\mathrm{85}\right),\:\mathrm{0}\:\leqslant\:{t}\:\leqslant\:\mathrm{28} \\ $$$$\left(\mathrm{a}\right)\:{f}\left(\mathrm{7}\right)\:=\:−\mathrm{0}.\mathrm{005}\left(\mathrm{7}−\mathrm{12}\right)\left(\mathrm{7}\:+\:\mathrm{13}\right)\left(\mathrm{7}\:+\:\mathrm{0}.\mathrm{85}\right)\:=\:\mathrm{11}.\mathrm{35}\:\mathrm{grams}/\mathrm{hour} \\ $$$$\mathcal{D}\mathrm{o}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{fof}\:{t}\:=\:\mathrm{13}\:\mathrm{h},\:{t}\:=\:\mathrm{17}\:\mathrm{hours},\:{t}\:=\:\mathrm{26}\:\mathrm{hours}. \\ $$$$\left(\mathrm{b}\right)\:\mathrm{when}\:\mathrm{the}\:\mathrm{growth}\:\mathrm{rate}\:\mathrm{is}\:\mathrm{0}\:,\:\mathrm{the}\:{f}\left({t}\right)\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:−\mathrm{0}.\mathrm{005}\left({t}\:−\mathrm{12}\right)\left({t}\:+\mathrm{3}\right)\left({t}\:+\:\mathrm{0}.\mathrm{85}\right)\:=\:\mathrm{0}\:\Rightarrow\:{t}\:=\:\mathrm{12}\:\mathrm{h} \\ $$$$\mathrm{at}\:{t}\:=\:\mathrm{0},\:{f}\left(\mathrm{0}\right)\:=\:−\mathrm{0}.\mathrm{005}\left(−\mathrm{12}\right)\left(\mathrm{3}\right)\left(\mathrm{0}.\mathrm{85}\right)\:=\:\mathrm{0}.\mathrm{05} \\ $$$$\left(\mathrm{d}\right)\:{f}\:'\left({t}\right)\:>\:\mathrm{0}\:\mathrm{and}\:{f}\:'\left({t}\right)\:<\:\mathrm{0} \\ $$
Answered by Rio Michael last updated on 12/Jun/20
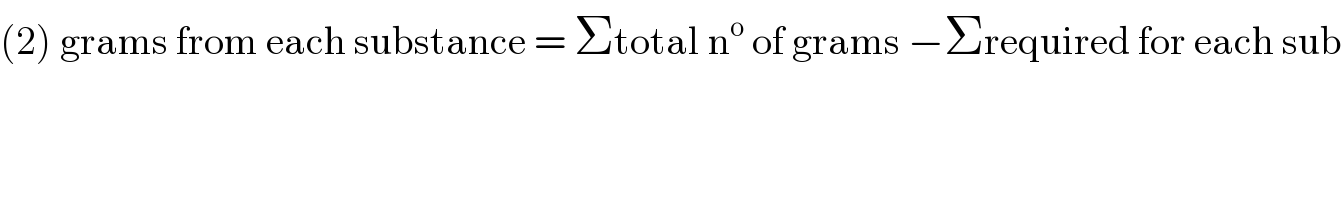
$$\left(\mathrm{2}\right)\:\mathrm{grams}\:\mathrm{from}\:\mathrm{each}\:\mathrm{substance}\:=\:\Sigma\mathrm{total}\:\mathrm{n}^{\mathrm{o}} \:\mathrm{of}\:\mathrm{grams}\:−\Sigma\mathrm{required}\:\mathrm{for}\:\mathrm{each}\:\mathrm{sub} \\ $$$$ \\ $$
