Question Number 98342 by Lekhraj last updated on 13/Jun/20

Commented by MJS last updated on 13/Jun/20

$$\mathrm{29} \\ $$$${n}=\mathrm{29}+\mathrm{30}{k} \\ $$
Commented by Lekhraj last updated on 13/Jun/20

$$\mathrm{How}?\mathrm{Explain} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Jun/20

$$\mathrm{1}+\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +…+\mathrm{2}^{{n}} \equiv\mathrm{0}\left({mod}\:\mathrm{77}\right) \\ $$$$\Rightarrow\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{77}\right) \\ $$$$\Rightarrow\mathrm{2}^{{n}+\mathrm{1}} \equiv\mathrm{1}\left({mod}\:\mathrm{77}\right) \\ $$$$\mathrm{Observing}\:\mathrm{all}\:\mathrm{powers}\:\mathrm{of}\:\mathrm{2}\: \\ $$$$\left(\mathrm{2},\mathrm{2}^{\mathrm{2}} ,…,\mathrm{2}^{\mathrm{30}} \right)\mathrm{we}\:\mathrm{achieve}\:\mathrm{that} \\ $$$$\mathrm{2}^{\mathrm{30}} \mathrm{is}\:\mathrm{smallest}\:\mathrm{power}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\:\:\mathrm{2}^{\mathrm{30}} \equiv\mathrm{1}\left({mod}\:\mathrm{77}\right) \\ $$$$\therefore\:{n}+\mathrm{1}=\mathrm{30}\Rightarrow{n}=\mathrm{29} \\ $$
Commented by MJS last updated on 17/Jun/20
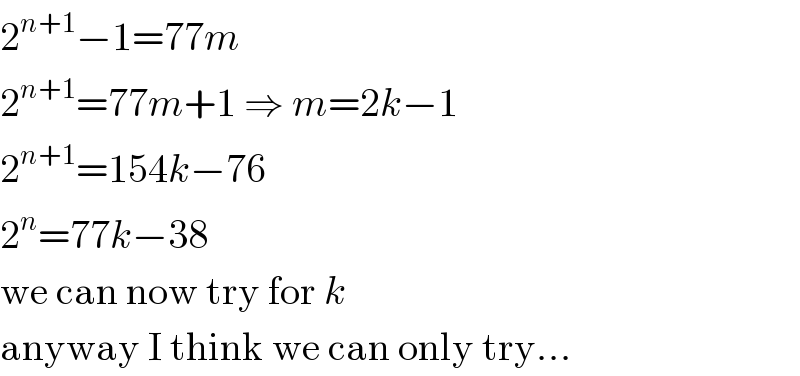
$$\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}=\mathrm{77}{m} \\ $$$$\mathrm{2}^{{n}+\mathrm{1}} =\mathrm{77}{m}+\mathrm{1}\:\Rightarrow\:{m}=\mathrm{2}{k}−\mathrm{1} \\ $$$$\mathrm{2}^{{n}+\mathrm{1}} =\mathrm{154}{k}−\mathrm{76} \\ $$$$\mathrm{2}^{{n}} =\mathrm{77}{k}−\mathrm{38} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{now}\:\mathrm{try}\:\mathrm{for}\:{k} \\ $$$$\mathrm{anyway}\:\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try}… \\ $$
Commented by Rasheed.Sindhi last updated on 17/Jun/20
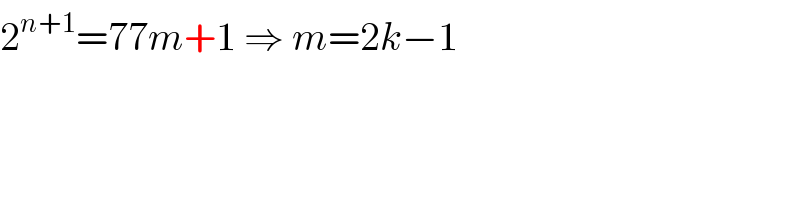
$$\mathrm{2}^{{n}+\mathrm{1}} =\mathrm{77}{m}+\mathrm{1}\:\Rightarrow\:{m}=\mathrm{2}{k}−\mathrm{1} \\ $$$$ \\ $$
Commented by MJS last updated on 17/Jun/20
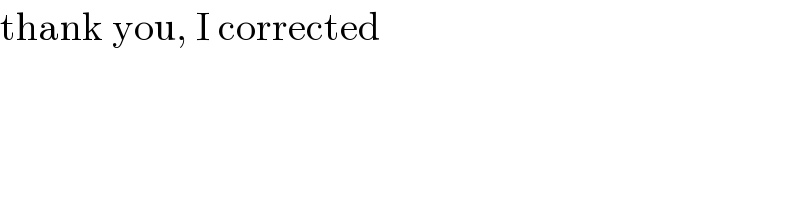
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{corrected} \\ $$
