Menu Close

Question-98355

Tinku Tara 0 Comments
Pin




Question Number 98355 by aurpeyz last updated on 13/Jun/20
Commented by aurpeyz last updated on 13/Jun/20
pls help me
$$\mathrm{pls}\:\mathrm{help}\:\mathrm{me} \\ $$
Answered by mr W last updated on 13/Jun/20
Commented by mr W last updated on 14/Jun/20
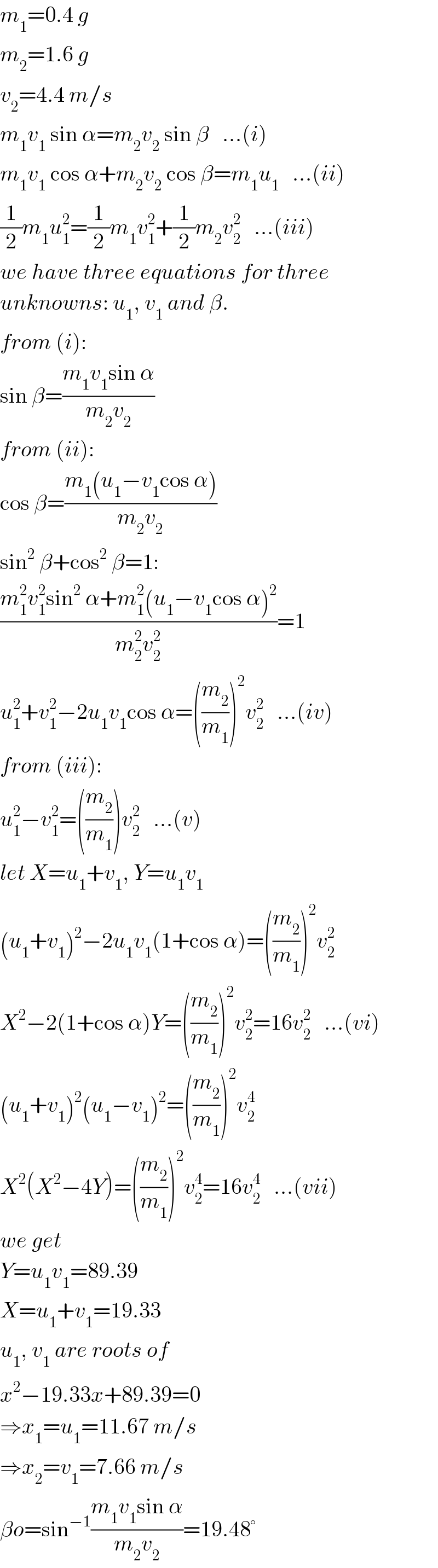
m_1 =0.4 g m_2 =1.6 g v_2 =4.4 m/s m_1 v_1 sin α=m_2 v_2 sin β ...(i) m_1 v_1 cos α+m_2 v_2 cos β=m_1 u_1 ...(ii) (1/2)m_1 u_1 ^2 =(1/2)m_1 v_1 ^2 +(1/2)m_2 v_2 ^2 ...(iii) we have three equations for three unknowns: u_1 , v_1 and β. from (i): sin β=((m_1 v_1 sin α)/(m_2 v_2 )) from (ii): cos β=((m_1 (u_1 −v_1 cos α))/(m_2 v_2 )) sin^2 β+cos^2 β=1: ((m_1 ^2 v_1 ^2 sin^2 α+m_1 ^2 (u_1 −v_1 cos α)^2 )/(m_2 ^2 v_2 ^2 ))=1 u_1 ^2 +v_1 ^2 −2u_1 v_1 cos α=((m_2 /m_1 ))^2 v_2 ^2 ...(iv) from (iii): u_1 ^2 −v_1 ^2 =((m_2 /m_1 ))v_2 ^2 ...(v) let X=u_1 +v_1 , Y=u_1 v_1 (u_1 +v_1 )^2 −2u_1 v_1 (1+cos α)=((m_2 /m_1 ))^2 v_2 ^2 X^2 −2(1+cos α)Y=((m_2 /m_1 ))^2 v_2 ^2 =16v_2 ^2 ...(vi) (u_1 +v_1 )^2 (u_1 −v_1 )^2 =((m_2 /m_1 ))^2 v_2 ^4 X^2 (X^2 −4Y)=((m_2 /m_1 ))^2 v_2 ^4 =16v_2 ^4 ...(vii) we get Y=u_1 v_1 =89.39 X=u_1 +v_1 =19.33 u_1 , v_1 are roots of x^2 −19.33x+89.39=0 ⇒x_1 =u_1 =11.67 m/s ⇒x_2 =v_1 =7.66 m/s βo=sin^(−1) ((m_1 v_1 sin α)/(m_2 v_2 ))=19.48°
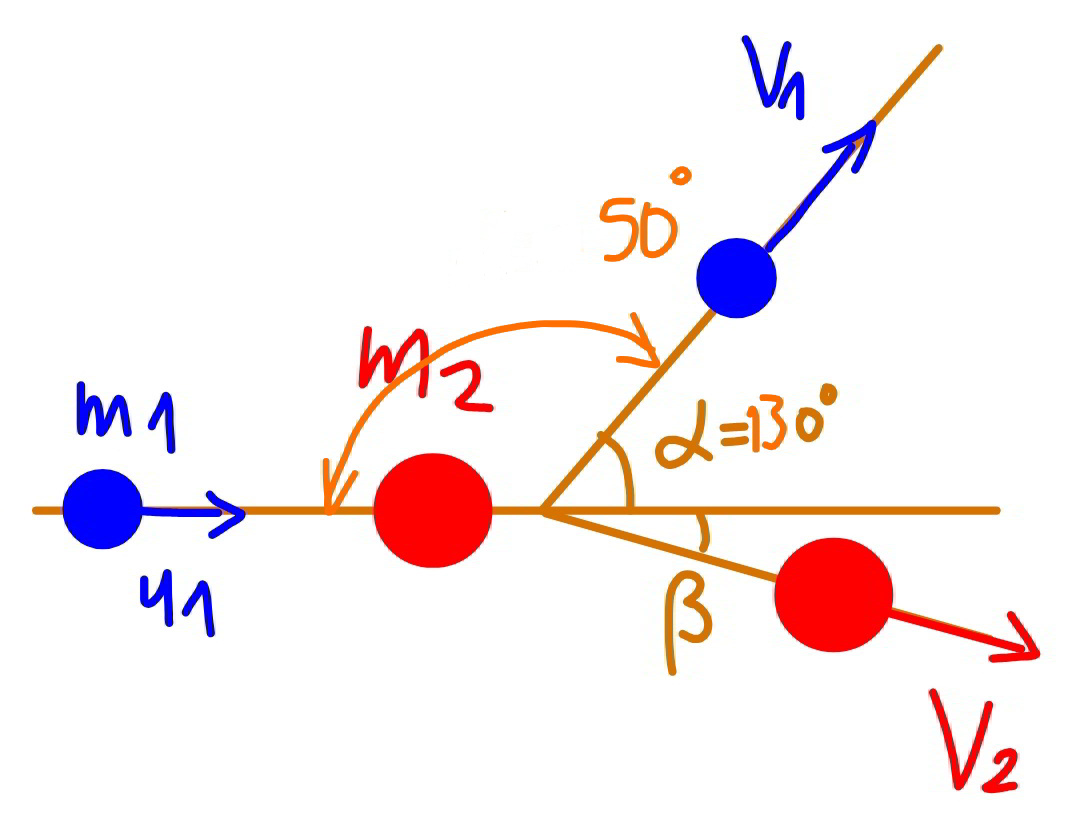
$${m}_{\mathrm{1}} =\mathrm{0}.\mathrm{4}\:{g} \\ $$$${m}_{\mathrm{2}} =\mathrm{1}.\mathrm{6}\:{g} \\ $$$${v}_{\mathrm{2}} =\mathrm{4}.\mathrm{4}\:{m}/{s} \\ $$$${m}_{\mathrm{1}} {v}_{\mathrm{1}} \:\mathrm{sin}\:\alpha={m}_{\mathrm{2}} {v}_{\mathrm{2}} \:\mathrm{sin}\:\beta\:\:\:…\left({i}\right) \\ $$$${m}_{\mathrm{1}} {v}_{\mathrm{1}} \:\mathrm{cos}\:\alpha+{m}_{\mathrm{2}} {v}_{\mathrm{2}} \:\mathrm{cos}\:\beta={m}_{\mathrm{1}} {u}_{\mathrm{1}} \:\:\:…\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}} {u}_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}} {v}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${we}\:{have}\:{three}\:{equations}\:{for}\:{three} \\ $$$${unknowns}:\:{u}_{\mathrm{1}} ,\:{v}_{\mathrm{1}} \:{and}\:\beta. \\ $$$${from}\:\left({i}\right): \\ $$$$\mathrm{sin}\:\beta=\frac{{m}_{\mathrm{1}} {v}_{\mathrm{1}} \mathrm{sin}\:\alpha}{{m}_{\mathrm{2}} {v}_{\mathrm{2}} } \\ $$$${from}\:\left({ii}\right): \\ $$$$\mathrm{cos}\:\beta=\frac{{m}_{\mathrm{1}} \left({u}_{\mathrm{1}} −{v}_{\mathrm{1}} \mathrm{cos}\:\alpha\right)}{{m}_{\mathrm{2}} {v}_{\mathrm{2}} } \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\beta+\mathrm{cos}^{\mathrm{2}} \:\beta=\mathrm{1}: \\ $$$$\frac{{m}_{\mathrm{1}} ^{\mathrm{2}} {v}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+{m}_{\mathrm{1}} ^{\mathrm{2}} \left({u}_{\mathrm{1}} −{v}_{\mathrm{1}} \mathrm{cos}\:\alpha\right)^{\mathrm{2}} }{{m}_{\mathrm{2}} ^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{2}} }=\mathrm{1} \\ $$$${u}_{\mathrm{1}} ^{\mathrm{2}} +{v}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{u}_{\mathrm{1}} {v}_{\mathrm{1}} \mathrm{cos}\:\alpha=\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:…\left({iv}\right) \\ $$$${from}\:\left({iii}\right): \\ $$$${u}_{\mathrm{1}} ^{\mathrm{2}} −{v}_{\mathrm{1}} ^{\mathrm{2}} =\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right){v}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:…\left({v}\right) \\ $$$${let}\:{X}={u}_{\mathrm{1}} +{v}_{\mathrm{1}} ,\:{Y}={u}_{\mathrm{1}} {v}_{\mathrm{1}} \\ $$$$\left({u}_{\mathrm{1}} +{v}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{2}{u}_{\mathrm{1}} {v}_{\mathrm{1}} \left(\mathrm{1}+\mathrm{cos}\:\alpha\right)=\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${X}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right){Y}=\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{16}{v}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:…\left({vi}\right) \\ $$$$\left({u}_{\mathrm{1}} +{v}_{\mathrm{1}} \right)^{\mathrm{2}} \left({u}_{\mathrm{1}} −{v}_{\mathrm{1}} \right)^{\mathrm{2}} =\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{4}} \\ $$$${X}^{\mathrm{2}} \left({X}^{\mathrm{2}} −\mathrm{4}{Y}\right)=\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{16}{v}_{\mathrm{2}} ^{\mathrm{4}} \:\:\:…\left({vii}\right) \\ $$$${we}\:{get} \\ $$$${Y}={u}_{\mathrm{1}} {v}_{\mathrm{1}} =\mathrm{89}.\mathrm{39} \\ $$$${X}={u}_{\mathrm{1}} +{v}_{\mathrm{1}} =\mathrm{19}.\mathrm{33} \\ $$$${u}_{\mathrm{1}} ,\:{v}_{\mathrm{1}} \:{are}\:{roots}\:{of} \\ $$$${x}^{\mathrm{2}} −\mathrm{19}.\mathrm{33}{x}+\mathrm{89}.\mathrm{39}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ={u}_{\mathrm{1}} =\mathrm{11}.\mathrm{67}\:{m}/{s} \\ $$$$\Rightarrow{x}_{\mathrm{2}} ={v}_{\mathrm{1}} =\mathrm{7}.\mathrm{66}\:{m}/{s} \\ $$$$\beta{o}=\mathrm{sin}^{−\mathrm{1}} \frac{{m}_{\mathrm{1}} {v}_{\mathrm{1}} \mathrm{sin}\:\alpha}{{m}_{\mathrm{2}} {v}_{\mathrm{2}} }=\mathrm{19}.\mathrm{48}° \\ $$
Commented by 1549442205 last updated on 14/Jun/20
we infer tan𝛃=((v_1 sin𝛂)/(u_1 −v_1 cos𝛂))(1) In above formula known v_1 =4.4,α=50° Dividing (4i)by (5i) we get ((u_1 ^2 +v_1 ^2 −2u_1 v_1 cosα)/(u_1 ^2 −v_1 ^2 ))=(m_2 /m_1 )=4 which gives us the quadratic with respect to u_1 3u_1 ^2 +2u_1 v_1 cosα−5v_1 ^2 =0(2) which has unique root u_1 =4.8153(m/s) Replace into (1) we obtain: tanβ=1.69629⇒β≈59°28′
$$\mathrm{we}\:\mathrm{infer}\:\boldsymbol{\mathrm{tan}\beta}=\frac{\boldsymbol{\mathrm{v}}_{\mathrm{1}} \boldsymbol{\mathrm{sin}\alpha}}{\boldsymbol{\mathrm{u}}_{\mathrm{1}} −\boldsymbol{\mathrm{v}}_{\mathrm{1}} \boldsymbol{\mathrm{cos}\alpha}}\left(\mathrm{1}\right) \\ $$$$\mathrm{In}\:\mathrm{above}\:\mathrm{formula}\:\mathrm{known}\:\mathrm{v}_{\mathrm{1}} =\mathrm{4}.\mathrm{4},\alpha=\mathrm{50}° \\ $$$$\mathrm{Dividing}\:\left(\mathrm{4i}\right)\mathrm{by}\:\left(\mathrm{5i}\right)\:\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{u}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{v}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \mathrm{cos}\alpha}{\mathrm{u}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{v}_{\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{m}_{\mathrm{2}} }{\mathrm{m}_{\mathrm{1}} }=\mathrm{4} \\ $$$$\mathrm{which}\:\mathrm{gives}\:\mathrm{us}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{with}\:\mathrm{respect}\:\:\mathrm{to}\:\mathrm{u}_{\mathrm{1}} \\ $$$$\:\:\mathrm{3u}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \mathrm{cos}\alpha−\mathrm{5v}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{which}\:\mathrm{has}\:\mathrm{unique}\:\mathrm{root}\:\mathrm{u}_{\mathrm{1}} =\mathrm{4}.\mathrm{8153}\left(\mathrm{m}/\mathrm{s}\right) \\ $$$$\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{obtain}: \\ $$$$\mathrm{tan}\beta=\mathrm{1}.\mathrm{69629}\Rightarrow\beta\approx\mathrm{59}°\mathrm{28}' \\ $$
Commented by aurpeyz last updated on 13/Jun/20
no v1
$$\mathrm{no}\:\mathrm{v1} \\ $$
Commented by aurpeyz last updated on 13/Jun/20
is this the final answer Sir?
$$\mathrm{is}\:\mathrm{this}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{Sir}? \\ $$
Commented by mr W last updated on 13/Jun/20
i got the same result as given. i didn′t write all steps for the solution of equations. that′s not difficult. you can do it by yourself.
$${i}\:{got}\:{the}\:{same}\:{result}\:{as}\:{given}. \\ $$$${i}\:{didn}'{t}\:{write}\:{all}\:{steps}\:{for}\:{the}\:{solution} \\ $$$${of}\:{equations}.\:{that}'{s}\:{not}\:{difficult}.\:{you} \\ $$$${can}\:{do}\:{it}\:{by}\:{yourself}. \\ $$
Commented by 1549442205 last updated on 14/Jun/20
great work,thank prof.sir.I did a mistake
$$\mathrm{great}\:\mathrm{work},\mathrm{thank}\:\mathrm{prof}.\mathrm{sir}.\mathrm{I}\:\mathrm{did}\:\mathrm{a}\:\mathrm{mistake} \\ $$
Commented by mr W last updated on 14/Jun/20
i made the same mistake at first as you can see in my diagram, because i didn′t notice that m_2 >m_1 . when m_2 >m_1 , m_1 must move backwards after collision, i.e. the angle 50° is backwards, in the diagram α≠50°, but α=130°, then you can get a proper solution for the equations.
$${i}\:{made}\:{the}\:{same}\:{mistake}\:{at}\:{first}\:{as} \\ $$$${you}\:{can}\:{see}\:{in}\:{my}\:{diagram},\:{because}\:{i}\: \\ $$$${didn}'{t}\:{notice}\:{that}\:{m}_{\mathrm{2}} >{m}_{\mathrm{1}} .\:{when} \\ $$$${m}_{\mathrm{2}} >{m}_{\mathrm{1}} ,\:{m}_{\mathrm{1}} \:{must}\:{move}\:{backwards}\: \\ $$$${after}\:{collision},\:{i}.{e}.\:{the}\:{angle}\:\mathrm{50}°\:{is} \\ $$$${backwards},\:{in}\:{the}\:{diagram}\:\alpha\neq\mathrm{50}°, \\ $$$${but}\:\alpha=\mathrm{130}°,\:{then}\:{you}\:{can}\:{get}\:{a}\:{proper} \\ $$$${solution}\:{for}\:{the}\:{equations}. \\ $$
Commented by aurpeyz last updated on 14/Jun/20
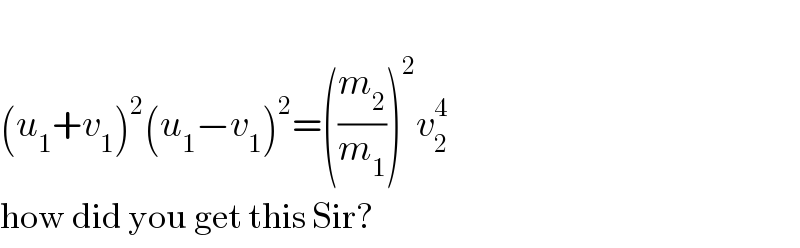
(u_1 +v_1 )^2 (u_1 −v_1 )^2 =((m_2 /m_1 ))^2 v_2 ^4 how did you get this Sir?
$$ \\ $$$$\left({u}_{\mathrm{1}} +{v}_{\mathrm{1}} \right)^{\mathrm{2}} \left({u}_{\mathrm{1}} −{v}_{\mathrm{1}} \right)^{\mathrm{2}} =\left(\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }\right)^{\mathrm{2}} {v}_{\mathrm{2}} ^{\mathrm{4}} \\ $$$$\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{this}\:\mathrm{Sir}? \\ $$
Commented by mr W last updated on 14/Jun/20
squaring eqn. (v)
$${squaring}\:{eqn}.\:\left({v}\right) \\ $$
Commented by aurpeyz last updated on 14/Jun/20
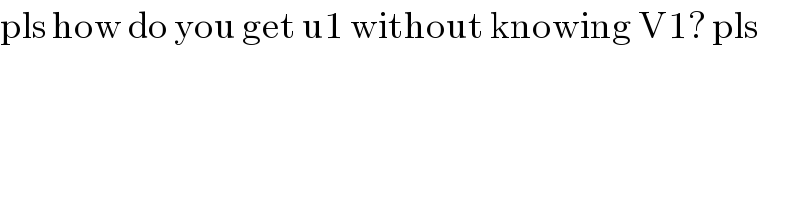
pls how do you get u1 without knowing V1? pls
$$\mathrm{pls}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}\:\mathrm{u1}\:\mathrm{without}\:\mathrm{knowing}\:\mathrm{V1}?\:\mathrm{pls} \\ $$
Commented by mr W last updated on 14/Jun/20
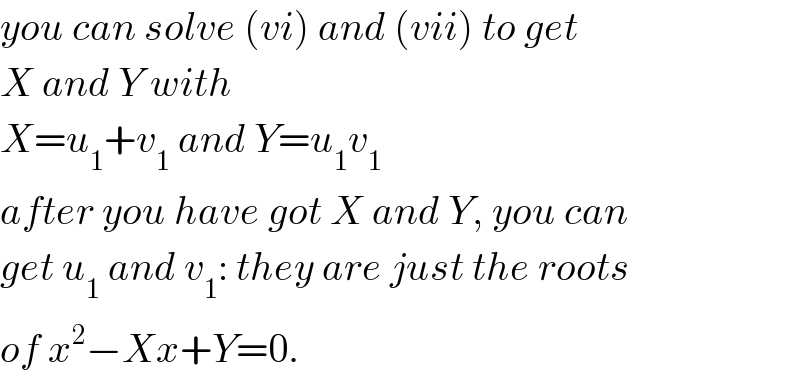
you can solve (vi) and (vii) to get X and Y with X=u_1 +v_1 and Y=u_1 v_1 after you have got X and Y, you can get u_1 and v_1 : they are just the roots of x^2 −Xx+Y=0.
$${you}\:{can}\:{solve}\:\left({vi}\right)\:{and}\:\left({vii}\right)\:{to}\:{get} \\ $$$${X}\:{and}\:{Y}\:{with}\: \\ $$$${X}={u}_{\mathrm{1}} +{v}_{\mathrm{1}} \:{and}\:{Y}={u}_{\mathrm{1}} {v}_{\mathrm{1}} \\ $$$${after}\:{you}\:{have}\:{got}\:{X}\:{and}\:{Y},\:{you}\:{can} \\ $$$${get}\:{u}_{\mathrm{1}} \:{and}\:{v}_{\mathrm{1}} :\:{they}\:{are}\:{just}\:{the}\:{roots} \\ $$$${of}\:{x}^{\mathrm{2}} −{Xx}+{Y}=\mathrm{0}. \\ $$
Commented by aurpeyz last updated on 14/Jun/20
i will work on that Sir. this is the best platform for learning sincerely
$$\mathrm{i}\:\mathrm{will}\:\mathrm{work}\:\mathrm{on}\:\mathrm{that}\:\mathrm{Sir}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{best}\:\mathrm{platform}\:\mathrm{for}\:\mathrm{learning}\:\mathrm{sincerely} \\ $$
Commented by mr W last updated on 14/Jun/20
just try sir! good luck! i showed only one of possible ways which i think is good for beginers to understand. maybe there are other better ways.
$${just}\:{try}\:{sir}!\:{good}\:{luck}! \\ $$$${i}\:{showed}\:{only}\:{one}\:{of}\:{possible}\:{ways} \\ $$$${which}\:{i}\:{think}\:{is}\:{good}\:{for}\:{beginers}\:{to} \\ $$$${understand}. \\ $$$${maybe}\:{there}\:{are}\:{other}\:{better}\:{ways}. \\ $$
Commented by aurpeyz last updated on 14/Jun/20
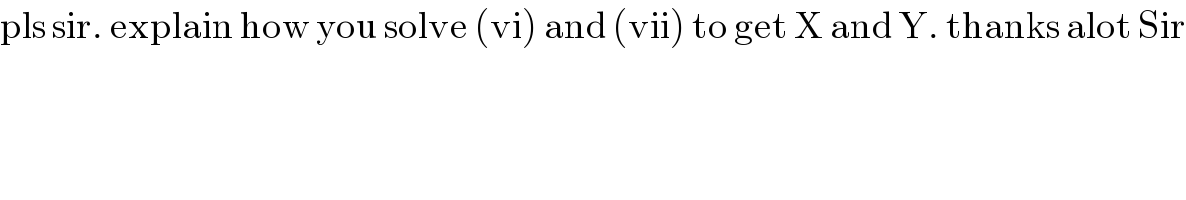
pls sir. explain how you solve (vi) and (vii) to get X and Y. thanks alot Sir
$$\mathrm{pls}\:\mathrm{sir}.\:\mathrm{explain}\:\mathrm{how}\:\mathrm{you}\:\mathrm{solve}\:\left(\mathrm{vi}\right)\:\mathrm{and}\:\left(\mathrm{vii}\right)\:\mathrm{to}\:\mathrm{get}\:\mathrm{X}\:\mathrm{and}\:\mathrm{Y}.\:\mathrm{thanks}\:\mathrm{alot}\:\mathrm{Sir} \\ $$
Commented by aurpeyz last updated on 14/Jun/20
hurray. i have gotten it Sir. thanks alot
$$\mathrm{hurray}.\:\mathrm{i}\:\mathrm{have}\:\mathrm{gotten}\:\mathrm{it}\:\mathrm{Sir}.\:\mathrm{thanks}\:\mathrm{alot} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *