Question Number 98408 by bemath last updated on 13/Jun/20
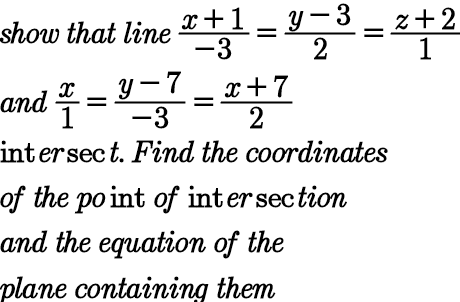
Answered by smridha last updated on 13/Jun/20
![for L_1 any point (p_1 )can be described as (−1−3t,3+2t,−2+t). for L_2 any point (p_2 ) can be described as (s,7−3s,−7+2s) [s and t are just two parameters] now if p_(1 ) and p_2 became same poit say (p) then we say the two lines are intersecting at point (p) so it is required that −1−3t=s ,3+2t=7−3s,−2+t=−7+2s solving first two we get.. t=−1 and s=2 now put it at 3rd one we get −2−1=−3 and −7+2×2=−3 so the two lines are intersecting at point p and its coordinate is P(2,1,−3) now the equation of plane that containing this two intersecting lines L_(1 ) and L_2 determinant (((x y−7 z+7)),((1 −3 2)),((−3 2 1)))=0 we get: x+y+z=0](https://www.tinkutara.com/question/Q98414.png)
$$\boldsymbol{{for}}\:\boldsymbol{{L}}_{\mathrm{1}} \:\boldsymbol{{any}}\:\boldsymbol{{point}}\:\left(\boldsymbol{{p}}_{\mathrm{1}} \right)\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{described}}\:\boldsymbol{{as}} \\ $$$$\left(−\mathrm{1}−\mathrm{3}\boldsymbol{{t}},\mathrm{3}+\mathrm{2}\boldsymbol{{t}},−\mathrm{2}+\boldsymbol{{t}}\right). \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{L}}_{\mathrm{2}} \boldsymbol{{any}}\:\boldsymbol{{point}}\:\left(\boldsymbol{{p}}_{\mathrm{2}} \right)\:\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{described}} \\ $$$$\boldsymbol{{as}}\:\left(\boldsymbol{{s}},\mathrm{7}−\mathrm{3}\boldsymbol{{s}},−\mathrm{7}+\mathrm{2}\boldsymbol{{s}}\right) \\ $$$$\left[\boldsymbol{{s}}\:\boldsymbol{{and}}\:\boldsymbol{{t}}\:\boldsymbol{{are}}\:\boldsymbol{{just}}\:\boldsymbol{{two}}\:\boldsymbol{{parameters}}\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{if}}\:\boldsymbol{{p}}_{\mathrm{1}\:} \boldsymbol{{and}}\:\boldsymbol{{p}}_{\mathrm{2}} \:\boldsymbol{{became}}\:\boldsymbol{{same}}\:\boldsymbol{{poit}} \\ $$$$\boldsymbol{{say}}\:\left(\boldsymbol{{p}}\right)\:\boldsymbol{{then}}\:\boldsymbol{{we}}\:\boldsymbol{{say}}\:\boldsymbol{{the}}\:\boldsymbol{{two}}\:\boldsymbol{{lines}} \\ $$$$\boldsymbol{{ar}}{e}\:\boldsymbol{{intersecting}}\:\boldsymbol{{at}}\:\boldsymbol{{point}}\:\left(\boldsymbol{{p}}\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{required}}\:\boldsymbol{{that}} \\ $$$$−\mathrm{1}−\mathrm{3}\boldsymbol{{t}}=\boldsymbol{{s}}\:,\mathrm{3}+\mathrm{2}\boldsymbol{{t}}=\mathrm{7}−\mathrm{3}\boldsymbol{{s}},−\mathrm{2}+\boldsymbol{{t}}=−\mathrm{7}+\mathrm{2}\boldsymbol{{s}} \\ $$$$\boldsymbol{{solving}}\:\boldsymbol{{first}}\:\boldsymbol{{two}}\:\boldsymbol{{we}}\:\boldsymbol{{get}}.. \\ $$$$\boldsymbol{{t}}=−\mathrm{1}\:\boldsymbol{{and}}\:\boldsymbol{{s}}=\mathrm{2} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{put}}\:\boldsymbol{{it}}\:\boldsymbol{{at}}\:\mathrm{3}\boldsymbol{{rd}}\:\boldsymbol{{one}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$−\mathrm{2}−\mathrm{1}=−\mathrm{3}\:\boldsymbol{{and}}\:−\mathrm{7}+\mathrm{2}×\mathrm{2}=−\mathrm{3} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{two}}\:\boldsymbol{{line}}{s}\:\boldsymbol{{are}}\:\boldsymbol{{intersecting}}\:\boldsymbol{{at}}\:\boldsymbol{{point}} \\ $$$$\boldsymbol{{p}}\:\boldsymbol{{and}}\:\boldsymbol{{its}}\:\boldsymbol{{coordinate}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{P}}\left(\mathrm{2},\mathrm{1},−\mathrm{3}\right) \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{the}}\:\boldsymbol{{equation}}\:\boldsymbol{{of}}\:\boldsymbol{{plane}} \\ $$$$\boldsymbol{{that}}\:\boldsymbol{{containing}}\:\boldsymbol{{this}}\:\boldsymbol{{t}}{w}\boldsymbol{{o}}\:\boldsymbol{{intersecting}} \\ $$$$\boldsymbol{{line}}{s}\:\boldsymbol{{L}}_{\mathrm{1}\:\:} \boldsymbol{{and}}\:\boldsymbol{{L}}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix}{\boldsymbol{{x}}\:\:\:\boldsymbol{{y}}−\mathrm{7}\:\:\boldsymbol{{z}}+\mathrm{7}}\\{\mathrm{1}\:\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\:\mathrm{2}}\\{−\mathrm{3}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}=\mathrm{0} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}}:\:\:\:\:\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}=\mathrm{0} \\ $$
