Question Number 98416 by 175 last updated on 13/Jun/20

Answered by Farruxjano last updated on 13/Jun/20
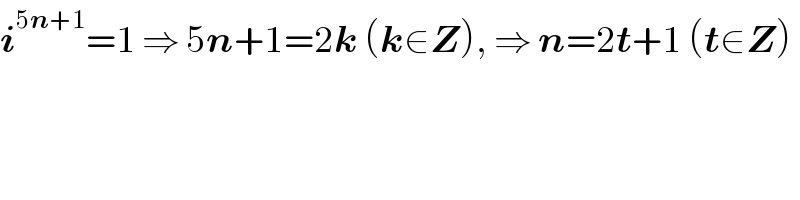
$$\boldsymbol{{i}}^{\mathrm{5}\boldsymbol{{n}}+\mathrm{1}} =\mathrm{1}\:\Rightarrow\:\mathrm{5}\boldsymbol{{n}}+\mathrm{1}=\mathrm{2}\boldsymbol{{k}}\:\left(\boldsymbol{{k}}\in\boldsymbol{{Z}}\right),\:\Rightarrow\:\boldsymbol{{n}}=\mathrm{2}\boldsymbol{{t}}+\mathrm{1}\:\left(\boldsymbol{{t}}\in\boldsymbol{{Z}}\right) \\ $$
Answered by Ramajunan last updated on 13/Jun/20
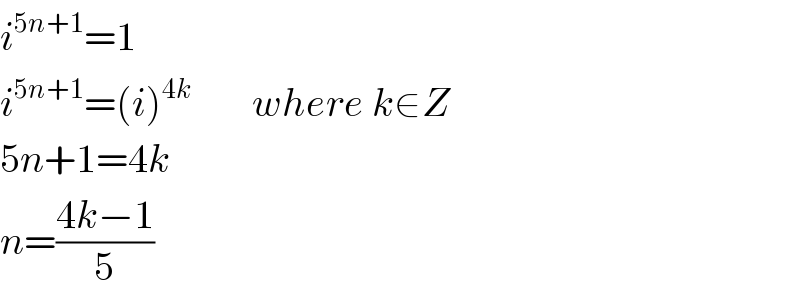
$${i}^{\mathrm{5}{n}+\mathrm{1}} =\mathrm{1} \\ $$$${i}^{\mathrm{5}{n}+\mathrm{1}} =\left({i}\right)^{\mathrm{4}{k}\:} \:\:\:\:\:\:\:{where}\:{k}\in{Z} \\ $$$$\mathrm{5}{n}+\mathrm{1}=\mathrm{4}{k} \\ $$$${n}=\frac{\mathrm{4}{k}−\mathrm{1}}{\mathrm{5}} \\ $$
Answered by mathmax by abdo last updated on 13/Jun/20
![i^(5n+1) =1 ⇒(e^((iπ)/2) )^(5n+1) =e^(i2kπ) ⇒ e^(i(5n+1)(π/2)) =e^(i2kπ ) ⇒(5n+1)(π/2)=2kπ ⇒ 5n+1 =4k ⇒5n =4k−1 let use congruence modul 5(prime) ⇒ 4k^− −1^− =0 ⇒−k^− −1 =0 [5] ⇒k =4 [5] ⇒k =5p+4 ⇒ 5n =20p+16−1 ⇒5n =20p+15 ⇒n =4p+3 so all number at form 4p+3 is solution](https://www.tinkutara.com/question/Q98422.png)
$$\mathrm{i}^{\mathrm{5n}+\mathrm{1}} \:=\mathrm{1}\:\Rightarrow\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)^{\mathrm{5n}+\mathrm{1}} \:=\mathrm{e}^{\mathrm{i2k}\pi} \:\Rightarrow\:\mathrm{e}^{\mathrm{i}\left(\mathrm{5n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}} \:=\mathrm{e}^{\mathrm{i2k}\pi\:} \:\Rightarrow\left(\mathrm{5n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}=\mathrm{2k}\pi\:\Rightarrow \\ $$$$\mathrm{5n}+\mathrm{1}\:=\mathrm{4k}\:\Rightarrow\mathrm{5n}\:=\mathrm{4k}−\mathrm{1}\:\:\mathrm{let}\:\mathrm{use}\:\mathrm{congruence}\:\mathrm{modul}\:\mathrm{5}\left(\mathrm{prime}\right)\:\Rightarrow \\ $$$$\mathrm{4}\overset{−} {\mathrm{k}}−\overset{−} {\mathrm{1}}\:=\mathrm{0}\:\Rightarrow−\overset{−} {\mathrm{k}}−\mathrm{1}\:=\mathrm{0}\:\left[\mathrm{5}\right]\:\Rightarrow\mathrm{k}\:=\mathrm{4}\:\left[\mathrm{5}\right]\:\Rightarrow\mathrm{k}\:=\mathrm{5p}+\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{5n}\:=\mathrm{20p}+\mathrm{16}−\mathrm{1}\:\Rightarrow\mathrm{5n}\:=\mathrm{20p}+\mathrm{15}\:\Rightarrow\mathrm{n}\:=\mathrm{4p}+\mathrm{3}\:\:\mathrm{so}\:\mathrm{all}\:\mathrm{number}\:\mathrm{at}\:\mathrm{form} \\ $$$$\mathrm{4p}+\mathrm{3}\:\mathrm{is}\:\mathrm{solution} \\ $$
