Question Number 98461 by mr W last updated on 14/Jun/20
Commented by mr W last updated on 14/Jun/20

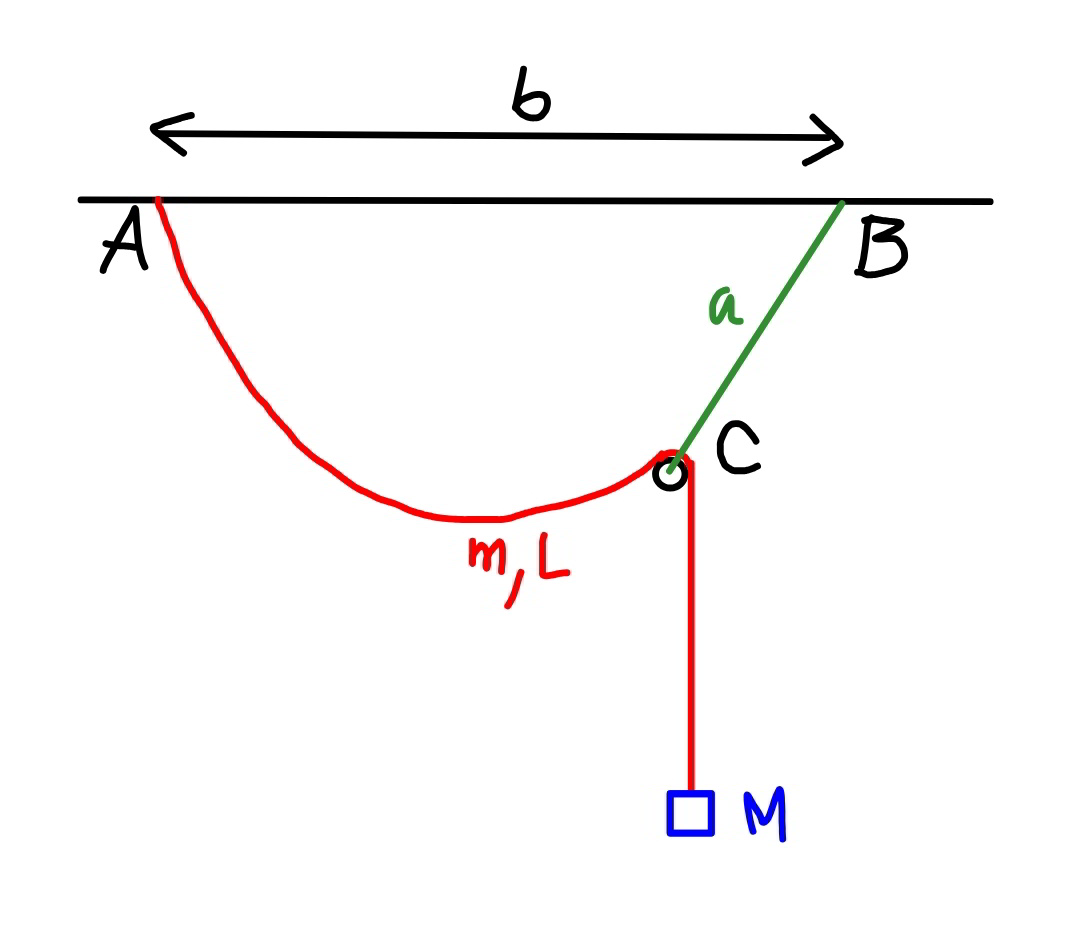
$${A}\:{long}\:{rope}\:{with}\:{mass}\:\boldsymbol{{m}}\:{and}\:{length}\: \\ $$$$\boldsymbol{{L}}\:{is}\:{fixed}\:{at}\:{one}\:{end}\:{on}\:{the}\:{ceiling} \\ $$$${at}\:{point}\:{A}.\:{At}\:{its}\:{other}\:{end}\:{a}\:{mass}\:\boldsymbol{{M}} \\ $$$${is}\:{connected}.\:{The}\:{long}\:{rope}\:{is}\:{hanged} \\ $$$${on}\:{the}\:{ceiling}\:{through}\:{an}\:{other}\:{thin}, \\ $$$${short}\:{and}\:{massless}\:{rope}\:{at}\:{point}\:{B}. \\ $$$${Find}\:{the}\:{tension}\:{in}\:{the}\:{short}\:{rope}. \\ $$
Answered by 1549442205 last updated on 14/Jun/20

Commented by 1549442205 last updated on 15/Jun/20
![Suppose that the rope L is tied at the end C so that AC=c.Then from Herong′s formula we have h_c =(2/b)(√(p(p−a)(p−b)(p−c))) ,where p=((a+b+c)/2).From that cos MCH^(�) =cosBCD^(�) =(h_c /a) i)Consider the case that a^2 +c^2 =b^2 we have cosMCH^(�) =cosBAC^(�) =(c/b)=((√(a^2 −b^2 ))/b).Henxe, The tension of the rope BC is T=CH=CM.cosMCH^(�) =(M+m)g.((√(b^2 −a^2 ))/b)(m−the mass of the rope L) ii)The case L≥c≥a^2 +b^2 then T=(M+m)g because CB⊥AB ]](https://www.tinkutara.com/question/Q98563.png)
$$\mathrm{Suppose}\:\mathrm{that}\:\mathrm{the}\:\mathrm{rope}\:\mathrm{L}\:\mathrm{is}\:\mathrm{tied}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}\:\mathrm{C} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{AC}=\mathrm{c}.\mathrm{Then}\:\mathrm{from}\:\mathrm{Herong}'\mathrm{s}\:\mathrm{formula}\: \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{h}_{\mathrm{c}} =\frac{\mathrm{2}}{\mathrm{b}}\sqrt{\mathrm{p}\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{b}\right)\left(\mathrm{p}−\mathrm{c}\right)}\:,\mathrm{where} \\ $$$$\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}}.\mathrm{From}\:\mathrm{that}\:\mathrm{cos}\:\widehat {\mathrm{MCH}}=\mathrm{cos}\widehat {\mathrm{BCD}}=\frac{\mathrm{h}_{\mathrm{c}} }{\mathrm{a}} \\ $$$$\left.\:\mathrm{i}\right)\mathrm{Consider}\:\mathrm{the}\:\mathrm{case}\:\mathrm{that}\:\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{cos}\widehat {\mathrm{MCH}}=\mathrm{cos}\widehat {\mathrm{BAC}}=\frac{\mathrm{c}}{\mathrm{b}}=\frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}{\mathrm{b}}.\mathrm{Henxe}, \\ $$$$\mathrm{The}\:\mathrm{tension}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}\:\mathrm{BC}\:\mathrm{is} \\ $$$$\boldsymbol{\mathrm{T}}=\boldsymbol{\mathrm{CH}}=\boldsymbol{\mathrm{CM}}.\boldsymbol{\mathrm{cos}}\widehat {\boldsymbol{\mathrm{MCH}}}=\left(\boldsymbol{\mathrm{M}}+\boldsymbol{\mathrm{m}}\right)\boldsymbol{\mathrm{g}}.\frac{\sqrt{\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}{\boldsymbol{\mathrm{b}}}\left(\boldsymbol{\mathrm{m}}−\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{mass}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{rope}}\:\boldsymbol{\mathrm{L}}\right) \\ $$$$\left.\:\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{case}}\:\:\boldsymbol{\mathrm{L}}\geqslant\boldsymbol{\mathrm{c}}\geqslant\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{T}}=\left(\boldsymbol{\mathrm{M}}+\boldsymbol{\mathrm{m}}\right)\boldsymbol{\mathrm{g}}\:\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{CB}}\bot\boldsymbol{\mathrm{AB}} \\ $$$$ \\ $$$$\left.\right] \\ $$
Commented by mr W last updated on 14/Jun/20

$${thank}\:{you}\:{sir}. \\ $$$${but}\:{it}'{s}\:{not}\:{correct}. \\ $$$${the}\:{long}\:{rope}\:{has}\:{mass},\:{therefore} \\ $$$${AC}\:{is}\:{not}\:{a}\:{straight},\:{but}\:{a}\:{curve}. \\ $$
Commented by mr W last updated on 14/Jun/20

$${even}\:{if}\:{the}\:{long}\:{rope}\:{were}\:{massless}, \\ $$$${both}\:{ropes}\:{are}\:{not}\:{tied}\:{at}\:{point}\:{C}, \\ $$$${but}\:{connected}\:{with}\:{a}\:{small}\:{pulley}, \\ $$$${that}\:{means}\:{length}\:{c}\:{is}\:{not}\:{given},\:{but} \\ $$$${to}\:{determine}\:{from}\:{the}\:{condition}\:{that} \\ $$$${the}\:{tension}\:{in}\:{AC}\:{is}\:{equal}\:{to}\:{the} \\ $$$${tension}\:{in}\:{CM}. \\ $$
Answered by mr W last updated on 15/Jun/20

Commented by mr W last updated on 15/Jun/20
![case m=0, i.e. long rope massless 2β+(π/2)−α=π ⇒α=2β−(π/2) (a/(sin α))=(b/(sin (α+(π/2)−β))) −(a/(cos 2β))=(b/(sin β)) −(a/(1−2 sin^2 β))=(b/(sin β)) 2 sin^2 β−(a/b) sin β−1=0 ⇒sin β=(1/4)[(a/b)+(√(((a/b))^2 +8))] T_C =Mg T=2T_C cos β ⇒T=2Mg (√(1−(1/(16))[(a/b)+(√(((a/b))^2 +8))]^2 ))](https://www.tinkutara.com/question/Q98647.png)
$${case}\:{m}=\mathrm{0},\:{i}.{e}.\:{long}\:{rope}\:{massless} \\ $$$$\mathrm{2}\beta+\frac{\pi}{\mathrm{2}}−\alpha=\pi \\ $$$$\Rightarrow\alpha=\mathrm{2}\beta−\frac{\pi}{\mathrm{2}} \\ $$$$\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{2}}−\beta\right)} \\ $$$$−\frac{{a}}{\mathrm{cos}\:\mathrm{2}\beta}=\frac{{b}}{\mathrm{sin}\:\beta} \\ $$$$−\frac{{a}}{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\frac{{b}}{\mathrm{sin}\:\beta} \\ $$$$\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta−\frac{{a}}{{b}}\:\mathrm{sin}\:\beta−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{{a}}{{b}}+\sqrt{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{8}}\right] \\ $$$${T}_{{C}} ={Mg} \\ $$$${T}=\mathrm{2}{T}_{{C}} \:\mathrm{cos}\:\beta \\ $$$$\Rightarrow{T}=\mathrm{2}{Mg}\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}\left[\frac{{a}}{{b}}+\sqrt{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{8}}\right]^{\mathrm{2}} } \\ $$
Answered by mr W last updated on 15/Jun/20

Commented by mr W last updated on 15/Jun/20

$${case}\:{m}\neq\mathrm{0} \\ $$
Commented by mr W last updated on 16/Jun/20
![in this case the rope section AC is a part of the catenary. y=h cosh (x/h) with h=(T_0 /(ρg))=((T_C cos α)/(ρg)) and ρ=(m/L) α=(π/2)−2β tan α=y′=sinh (e/h)=(1/(tan 2β)) ⇒e=h sinh^(−1) (1/(tan 2β)) f=h cosh (e/h)=h cosh (sinh^(−1) (1/(tan 2β))) c=b−a sin β−e=b−a sin β−h sinh^(−1) (1/(tan 2β)) rope length AE^(⌢) =s_1 s_1 =h sinh (c/h)=h sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β))) rope length EC^(⌢) =s_2 s_2 =h sinh (e/h)=(h/(tan 2β)) rope length CD=s_3 s_3 =L−s_1 −s_2 s_3 =L−h sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β)))−(h/(tan 2β)) T_C =Mg+ρgs_3 T_C =Mg+ρg[L−h sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β)))−(h/(tan 2β))] T_C =(M+m)g−hρg[ sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β)))+(1/(tan 2β))] ((hρg)/(sin 2β))=(M+m)g−hρg[ sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β)))+(1/(tan 2β))] ((1+cos 2β)/(sin 2β))=(((M+m)L)/(mh))−sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β))) ⇒sinh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β))) =(((M+m)L)/(mh))−((1+cos 2β)/(sin 2β)) ...(i) d=f+a cos β h cosh (c/h)=h cosh (sinh^(−1) (1/(tan 2β)))+a cos β ⇒cosh (((b−a sin β)/h)−sinh^(−1) (1/(tan 2β)))=cosh (sinh^(−1) (1/(tan 2β)))+(a/h) cos β ...(ii) ⇒[cosh (sinh^(−1) (1/(tan 2β)))+(a/h) cos β]^2 −[(((M+m)L)/(mh))−((1+cos 2β)/(sin 2β))]^2 =1 ⇒[cosh (sinh^(−1) (1/(tan 2β))) h+a cos β]^2 −[(((M+m)L)/m)−(((1+cos 2β)/(sin 2β)))h]^2 =h^2 ⇒[cosh (sinh^(−1) (1/(tan 2β)))]^2 h^2 +a^2 cos^2 β+2a cos β cosh (sinh^(−1) (1/(tan 2β)))h−[(((M+m)L)/m)]^2 −(((1+cos 2β)/(sin 2β)))^2 h^2 +2(((1+cos 2β)/(sin 2β)))(((M+m)L)/m)h=h^2 ⇒(((1+2 cos 2β)/(sin^2 2β)))h^2 −(1/(sin β))[a(√(1+cos^2 2β))+(((1+cos 2β)/(cos β)))((M/m)+1)L]h+[(((M+m)L)/m)]^2 −a^2 cos^2 β=0 ...(iii) from (iii) we get h in terms of β. put this into (i) or (ii) we get β. T_C =((ρgh)/(sin 2β)) ⇒T=2T_C cos β=((ρgh)/(sin β))](https://www.tinkutara.com/question/Q98745.png)
$${in}\:{this}\:{case}\:{the}\:{rope}\:{section}\:{AC}\:{is} \\ $$$${a}\:{part}\:{of}\:{the}\:{catenary}. \\ $$$${y}={h}\:\mathrm{cosh}\:\frac{{x}}{{h}} \\ $$$${with}\:{h}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{{T}_{{C}} \mathrm{cos}\:\alpha}{\rho{g}}\:{and}\:\rho=\frac{{m}}{{L}} \\ $$$$\alpha=\frac{\pi}{\mathrm{2}}−\mathrm{2}\beta \\ $$$$\mathrm{tan}\:\alpha={y}'=\mathrm{sinh}\:\frac{{e}}{{h}}=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta} \\ $$$$\Rightarrow{e}={h}\:\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta} \\ $$$${f}={h}\:\mathrm{cosh}\:\frac{{e}}{{h}}={h}\:\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right) \\ $$$${c}={b}−{a}\:\mathrm{sin}\:\beta−{e}={b}−{a}\:\mathrm{sin}\:\beta−{h}\:\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta} \\ $$$${rope}\:{length}\:\overset{\frown} {{AE}}={s}_{\mathrm{1}} \\ $$$${s}_{\mathrm{1}} ={h}\:\mathrm{sinh}\:\frac{{c}}{{h}}={h}\:\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right) \\ $$$${rope}\:{length}\:\overset{\frown} {{EC}}={s}_{\mathrm{2}} \\ $$$${s}_{\mathrm{2}} ={h}\:\mathrm{sinh}\:\frac{{e}}{{h}}=\frac{{h}}{\mathrm{tan}\:\mathrm{2}\beta} \\ $$$${rope}\:{length}\:{CD}={s}_{\mathrm{3}} \\ $$$${s}_{\mathrm{3}} ={L}−{s}_{\mathrm{1}} −{s}_{\mathrm{2}} \\ $$$${s}_{\mathrm{3}} ={L}−{h}\:\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)−\frac{{h}}{\mathrm{tan}\:\mathrm{2}\beta} \\ $$$${T}_{{C}} ={Mg}+\rho{gs}_{\mathrm{3}} \\ $$$${T}_{{C}} ={Mg}+\rho{g}\left[{L}−{h}\:\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)−\frac{{h}}{\mathrm{tan}\:\mathrm{2}\beta}\right] \\ $$$${T}_{{C}} =\left({M}+{m}\right){g}−{h}\rho{g}\left[\:\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right] \\ $$$$\frac{{h}\rho{g}}{\mathrm{sin}\:\mathrm{2}\beta}=\left({M}+{m}\right){g}−{h}\rho{g}\left[\:\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right] \\ $$$$\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}=\frac{\left({M}+{m}\right){L}}{{mh}}−\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right) \\ $$$$\Rightarrow\mathrm{sinh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)\:=\frac{\left({M}+{m}\right){L}}{{mh}}−\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${d}={f}+{a}\:\mathrm{cos}\:\beta \\ $$$${h}\:\mathrm{cosh}\:\frac{{c}}{{h}}={h}\:\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)+{a}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow\mathrm{cosh}\:\left(\frac{{b}−{a}\:\mathrm{sin}\:\beta}{{h}}−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)=\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)+\frac{{a}}{{h}}\:\mathrm{cos}\:\beta\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\left[\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)+\frac{{a}}{{h}}\:\mathrm{cos}\:\beta\right]^{\mathrm{2}} −\left[\frac{\left({M}+{m}\right){L}}{{mh}}−\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left[\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)\:{h}+{a}\:\mathrm{cos}\:\beta\right]^{\mathrm{2}} −\left[\frac{\left({M}+{m}\right){L}}{{m}}−\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}\right){h}\right]^{\mathrm{2}} ={h}^{\mathrm{2}} \\ $$$$\Rightarrow\left[\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right)\right]^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\beta+\mathrm{2}{a}\:\mathrm{cos}\:\beta\:\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\beta}\right){h}−\left[\frac{\left({M}+{m}\right){L}}{{m}}\right]^{\mathrm{2}} −\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}\right)^{\mathrm{2}} {h}^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{2}\beta}\right)\frac{\left({M}+{m}\right){L}}{{m}}{h}={h}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\beta}\right){h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{sin}\:\beta}\left[{a}\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\beta}+\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{cos}\:\beta}\right)\left(\frac{{M}}{{m}}+\mathrm{1}\right){L}\right]{h}+\left[\frac{\left({M}+{m}\right){L}}{{m}}\right]^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\beta=\mathrm{0}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${from}\:\left({iii}\right)\:{we}\:{get}\:{h}\:{in}\:{terms}\:{of}\:\beta. \\ $$$${put}\:{this}\:{into}\:\left({i}\right)\:{or}\:\left({ii}\right)\:{we}\:{get}\:\beta. \\ $$$$ \\ $$$${T}_{{C}} =\frac{\rho{gh}}{\mathrm{sin}\:\mathrm{2}\beta} \\ $$$$\Rightarrow{T}=\mathrm{2}{T}_{{C}} \mathrm{cos}\:\beta=\frac{\rho{gh}}{\mathrm{sin}\:\beta} \\ $$
