Question Number 98463 by pranesh last updated on 14/Jun/20
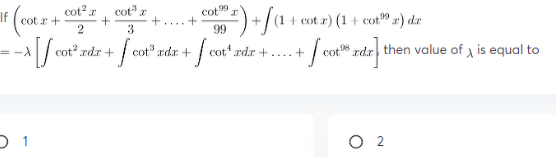
Answered by maths mind last updated on 15/Jun/20
![Σ_(k=1) ^(99) (x^k /k)=∫((1−x^(99) )/(1−x))dx (cot(x)+......+((cot^(99) (x))/(99)))+∫(1+cot(x))(1+cot^(99) (x))dx Σ_(n≥1) ((cot^n (x))/n)=Σ_(n≥1) (t^n /n)=∫((1−t^(99) )/(1−t))dt Σ((cot^k (x))/k)dx=∫((1−cot^(99) (x))/(1−cot(x))).(−1−cot^2 (x))dx we get ∫((1−cot^(99) (x))/(1−cot(x)))(−1−cot^2 (x))dx+∫(1+cot(x))(1+cot^(99) (x))dx =∫(((cot^(99) (x)−1)(1+cot^2 (x))+(1−cot^2 (x))(1+cot^(99) (x)))/(1−cot(x)))dx =∫((2cot^(99) (x)−2cot^2 (x))/(1−cot(x)))dx =−2∫cot^2 (x)((1−cot^(97) (x))/(1−cot(x)))dx =−2∫cot^2 (x).Σ_(k=0) ^(96) cot^k (x)dx =−2∫[cot^2 (x)+cot^3 (x)+.......+cot^(98) (x)]dx so λ=2](https://www.tinkutara.com/question/Q98725.png)
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\frac{{x}^{{k}} }{{k}}=\int\frac{\mathrm{1}−{x}^{\mathrm{99}} }{\mathrm{1}−{x}}{dx} \\ $$$$\left({cot}\left({x}\right)+……+\frac{{cot}^{\mathrm{99}} \left({x}\right)}{\mathrm{99}}\right)+\int\left(\mathrm{1}+{cot}\left({x}\right)\right)\left(\mathrm{1}+{cot}^{\mathrm{99}} \left({x}\right)\right){dx} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cot}^{{n}} \left({x}\right)}{{n}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{t}^{{n}} }{{n}}=\int\frac{\mathrm{1}−{t}^{\mathrm{99}} }{\mathrm{1}−{t}}{dt} \\ $$$$\Sigma\frac{{cot}^{{k}} \left({x}\right)}{{k}}{dx}=\int\frac{\mathrm{1}−{cot}^{\mathrm{99}} \left({x}\right)}{\mathrm{1}−{cot}\left({x}\right)}.\left(−\mathrm{1}−{cot}^{\mathrm{2}} \left({x}\right)\right){dx} \\ $$$${we}\:{get} \\ $$$$\int\frac{\mathrm{1}−{cot}^{\mathrm{99}} \left({x}\right)}{\mathrm{1}−{cot}\left({x}\right)}\left(−\mathrm{1}−{cot}^{\mathrm{2}} \left({x}\right)\right){dx}+\int\left(\mathrm{1}+{cot}\left({x}\right)\right)\left(\mathrm{1}+{cot}^{\mathrm{99}} \left({x}\right)\right){dx} \\ $$$$=\int\frac{\left({cot}^{\mathrm{99}} \left({x}\right)−\mathrm{1}\right)\left(\mathrm{1}+{cot}^{\mathrm{2}} \left({x}\right)\right)+\left(\mathrm{1}−{cot}^{\mathrm{2}} \left({x}\right)\right)\left(\mathrm{1}+{cot}^{\mathrm{99}} \left({x}\right)\right)}{\mathrm{1}−{cot}\left({x}\right)}{dx} \\ $$$$=\int\frac{\mathrm{2}{cot}^{\mathrm{99}} \left({x}\right)−\mathrm{2}{cot}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}−{cot}\left({x}\right)}{dx} \\ $$$$=−\mathrm{2}\int{cot}^{\mathrm{2}} \left({x}\right)\frac{\mathrm{1}−{cot}^{\mathrm{97}} \left({x}\right)}{\mathrm{1}−{cot}\left({x}\right)}{dx} \\ $$$$=−\mathrm{2}\int{cot}^{\mathrm{2}} \left({x}\right).\underset{{k}=\mathrm{0}} {\overset{\mathrm{96}} {\sum}}{cot}^{{k}} \left({x}\right){dx} \\ $$$$=−\mathrm{2}\int\left[{cot}^{\mathrm{2}} \left({x}\right)+{cot}^{\mathrm{3}} \left({x}\right)+…….+{cot}^{\mathrm{98}} \left({x}\right)\right]{dx} \\ $$$${so} \\ $$$$\lambda=\mathrm{2} \\ $$$$\: \\ $$
