Question Number 98506 by bemath last updated on 14/Jun/20
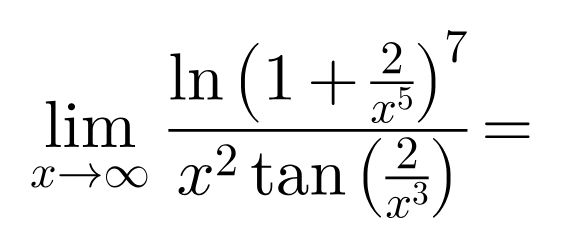
Commented by john santu last updated on 14/Jun/20
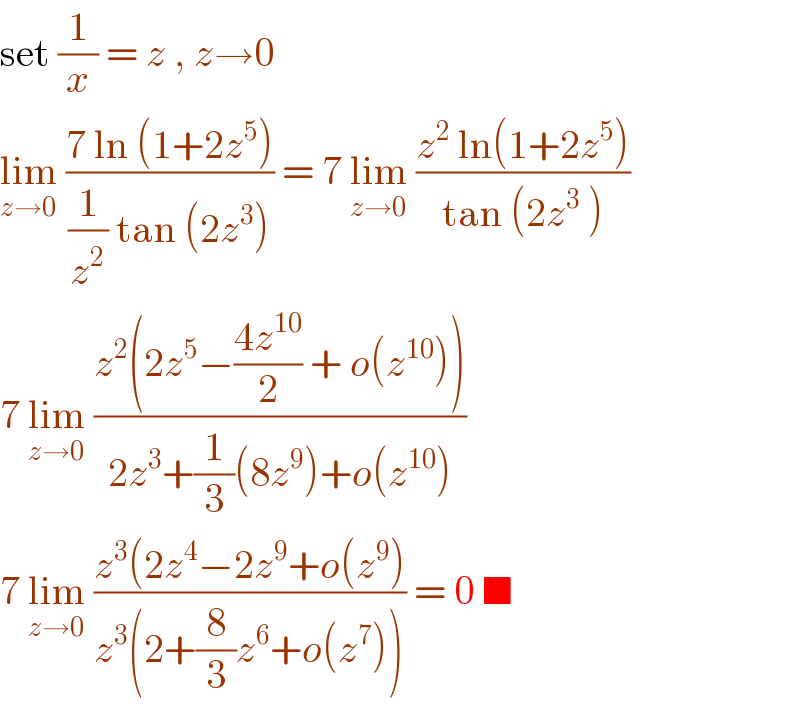
$$\mathrm{set}\:\frac{\mathrm{1}}{{x}}\:=\:{z}\:,\:{z}\rightarrow\mathrm{0} \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{7}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2}{z}^{\mathrm{5}} \right)}{\frac{\mathrm{1}}{{z}^{\mathrm{2}} }\:\mathrm{tan}\:\left(\mathrm{2}{z}^{\mathrm{3}} \right)}\:=\:\mathrm{7}\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{z}^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{2}{z}^{\mathrm{5}} \right)}{\mathrm{tan}\:\left(\mathrm{2}{z}^{\mathrm{3}} \:\right)} \\ $$$$\mathrm{7}\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{z}^{\mathrm{2}} \left(\mathrm{2}{z}^{\mathrm{5}} −\frac{\mathrm{4}{z}^{\mathrm{10}} }{\mathrm{2}}\:+\:{o}\left({z}^{\mathrm{10}} \right)\right)}{\mathrm{2}{z}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{8}{z}^{\mathrm{9}} \right)+{o}\left({z}^{\mathrm{10}} \right)} \\ $$$$\mathrm{7}\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{z}^{\mathrm{3}} \left(\mathrm{2}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{9}} +{o}\left({z}^{\mathrm{9}} \right)\right.}{{z}^{\mathrm{3}} \left(\mathrm{2}+\frac{\mathrm{8}}{\mathrm{3}}{z}^{\mathrm{6}} +{o}\left({z}^{\mathrm{7}} \right)\right)}\:=\:\mathrm{0}\:\blacksquare \\ $$
