Question-98516

Question Number 98516 by bemath last updated on 14/Jun/20

Commented by Aziztisffola last updated on 14/Jun/20

Hi sir best draw! which app do you use ?)=(√(x+(√(x+(√(x+...)))))) ⇔ f^2 (x)=x+f(x) I need the best one. x)−f(x)−x=0 =(−1)^2 −4×1×(−x)=1+4x ⇒ f(x)=((1+(√(1+4x)))/2) ( x and f(x) >0) f ′x)=(1/2) (4/(2(√(1+4x)))) = (1/( (√(1+4x)))) ′(5)=(1/( (√(1+4×5)))) = (1/( (√(21))))

$$\left.\:\mathrm{Hi}\:\mathrm{sir}\:\mathrm{best}\:\mathrm{draw}!\:\mathrm{which}\:\mathrm{app}\:\mathrm{do}\:\mathrm{you}\:\mathrm{use}\:?\right)=\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+…}}}\:\Leftrightarrow\:\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{x}+\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{I}\:\mathrm{need}\:\mathrm{the}\:\mathrm{best}\:\mathrm{one}. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}=\mathrm{0} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\left(−\mathrm{x}\right)=\mathrm{1}+\mathrm{4x} \\ $$$$\:\:\:\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}\:\:\:\left(\:\mathrm{x}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{x}\right)\:>\mathrm{0}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\mathrm{f}\:'\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4x}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4x}}} \\ $$$$\:'\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}×\mathrm{5}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by Quvonchbek last updated on 14/Jun/20

Answered by mr W last updated on 14/Jun/20

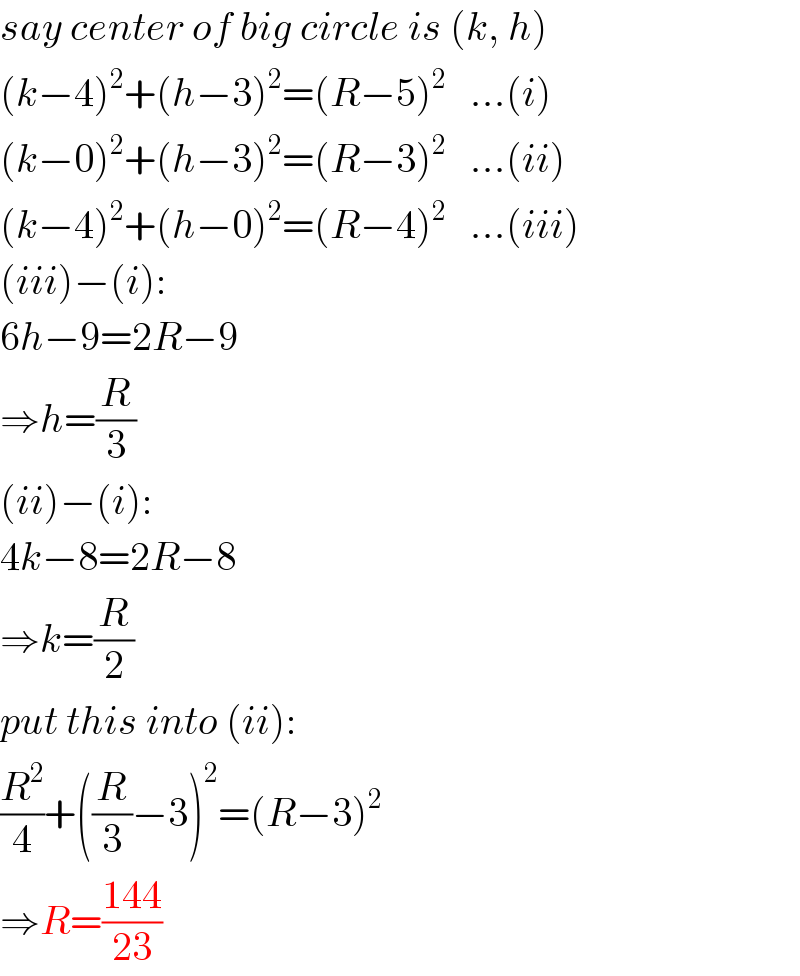
say center of big circle is (k, h) (k−4)^2 +(h−3)^2 =(R−5)^2 ...(i) (k−0)^2 +(h−3)^2 =(R−3)^2 ...(ii) (k−4)^2 +(h−0)^2 =(R−4)^2 ...(iii) (iii)−(i): 6h−9=2R−9 ⇒h=(R/3) (ii)−(i): 4k−8=2R−8 ⇒k=(R/2) put this into (ii): (R^2 /4)+((R/3)−3)^2 =(R−3)^2 ⇒R=((144)/(23))

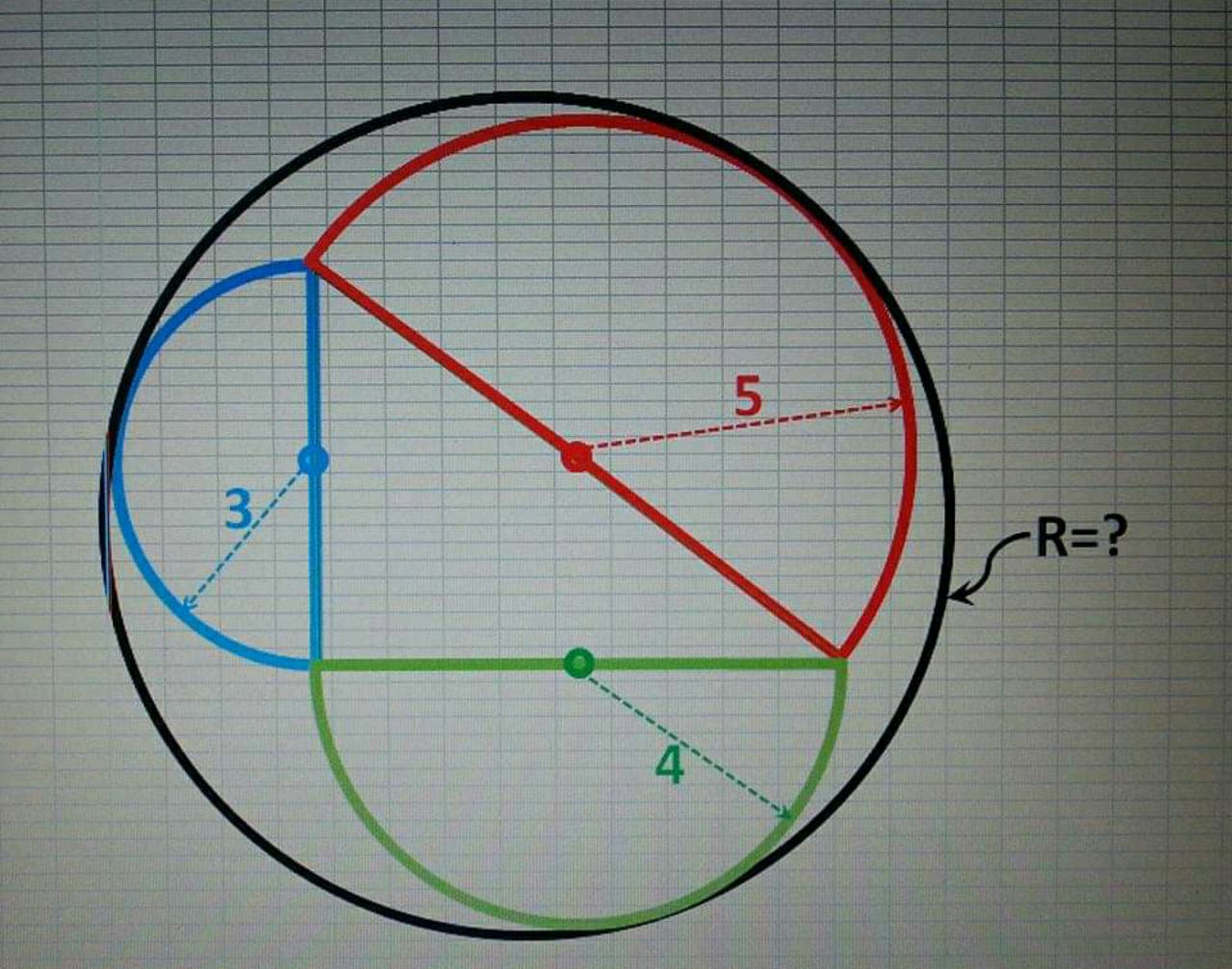
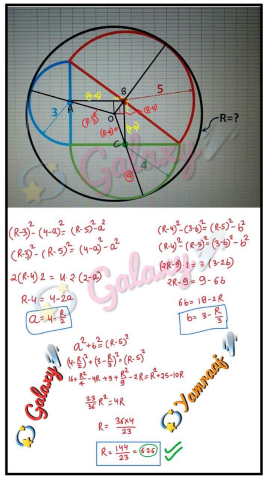
$${say}\:{center}\:{of}\:{big}\:{circle}\:{is}\:\left({k},\:{h}\right) \\ $$$$\left({k}−\mathrm{4}\right)^{\mathrm{2}} +\left({h}−\mathrm{3}\right)^{\mathrm{2}} =\left({R}−\mathrm{5}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left({k}−\mathrm{0}\right)^{\mathrm{2}} +\left({h}−\mathrm{3}\right)^{\mathrm{2}} =\left({R}−\mathrm{3}\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left({k}−\mathrm{4}\right)^{\mathrm{2}} +\left({h}−\mathrm{0}\right)^{\mathrm{2}} =\left({R}−\mathrm{4}\right)^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({iii}\right)−\left({i}\right): \\ $$$$\mathrm{6}{h}−\mathrm{9}=\mathrm{2}{R}−\mathrm{9} \\ $$$$\Rightarrow{h}=\frac{{R}}{\mathrm{3}} \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\mathrm{4}{k}−\mathrm{8}=\mathrm{2}{R}−\mathrm{8} \\ $$$$\Rightarrow{k}=\frac{{R}}{\mathrm{2}} \\ $$$${put}\:{this}\:{into}\:\left({ii}\right): \\ $$$$\frac{{R}^{\mathrm{2}} }{\mathrm{4}}+\left(\frac{{R}}{\mathrm{3}}−\mathrm{3}\right)^{\mathrm{2}} =\left({R}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{144}}{\mathrm{23}} \\ $$

Answered by john santu last updated on 14/Jun/20

Commented by john santu last updated on 14/Jun/20

(R−3)^2 =4^2 +(R−5)^2 −2×4×cos α (R−4)^2 =3^2 +(R−5)^2 −2×3×sin α [ sin^2 α=1−cos^2 α ] (((R−9)/(5(R−5))))^2 +(((R−8)/(2(R−5))))^2 =1 R = ((144)/(23)) .■

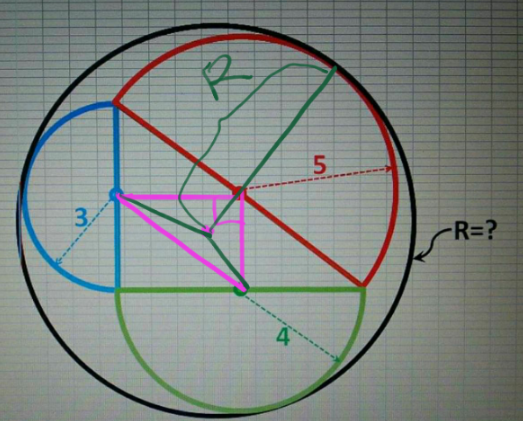
$$\left(\mathrm{R}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\left(\mathrm{R}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{4}×\mathrm{cos}\:\alpha \\ $$$$\left(\mathrm{R}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +\left(\mathrm{R}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{sin}\:\alpha \\ $$$$\left[\:\mathrm{sin}\:^{\mathrm{2}} \alpha=\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \alpha\:\right] \\ $$$$\left(\frac{\mathrm{R}−\mathrm{9}}{\mathrm{5}\left(\mathrm{R}−\mathrm{5}\right)}\right)^{\mathrm{2}} +\left(\frac{\mathrm{R}−\mathrm{8}}{\mathrm{2}\left(\mathrm{R}−\mathrm{5}\right)}\right)^{\mathrm{2}} =\mathrm{1}\: \\ $$$$\mathrm{R}\:=\:\frac{\mathrm{144}}{\mathrm{23}}\:.\blacksquare\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply