Question Number 98544 by abony1303 last updated on 14/Jun/20
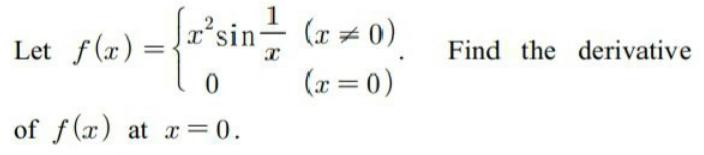
Commented by abony1303 last updated on 14/Jun/20

$$\mathrm{Pls}\:\mathrm{help} \\ $$
Answered by mathmax by abdo last updated on 14/Jun/20
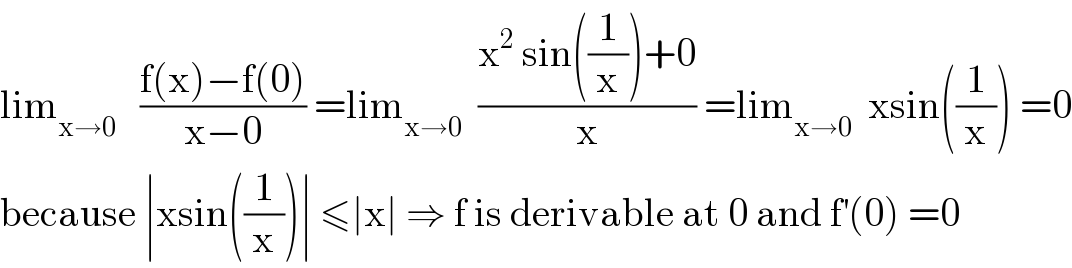
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{0}\right)}{\mathrm{x}−\mathrm{0}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{0}}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{xsin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\mathrm{0} \\ $$$$\mathrm{because}\:\mid\mathrm{xsin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mid\:\leqslant\mid\mathrm{x}\mid\:\Rightarrow\:\mathrm{f}\:\mathrm{is}\:\mathrm{derivable}\:\mathrm{at}\:\mathrm{0}\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{0}\right)\:=\mathrm{0} \\ $$
