Menu Close

Question-98596

Tinku Tara 0 Comments
Pin




Question Number 98596 by bemath last updated on 15/Jun/20
Commented by bobhans last updated on 15/Jun/20
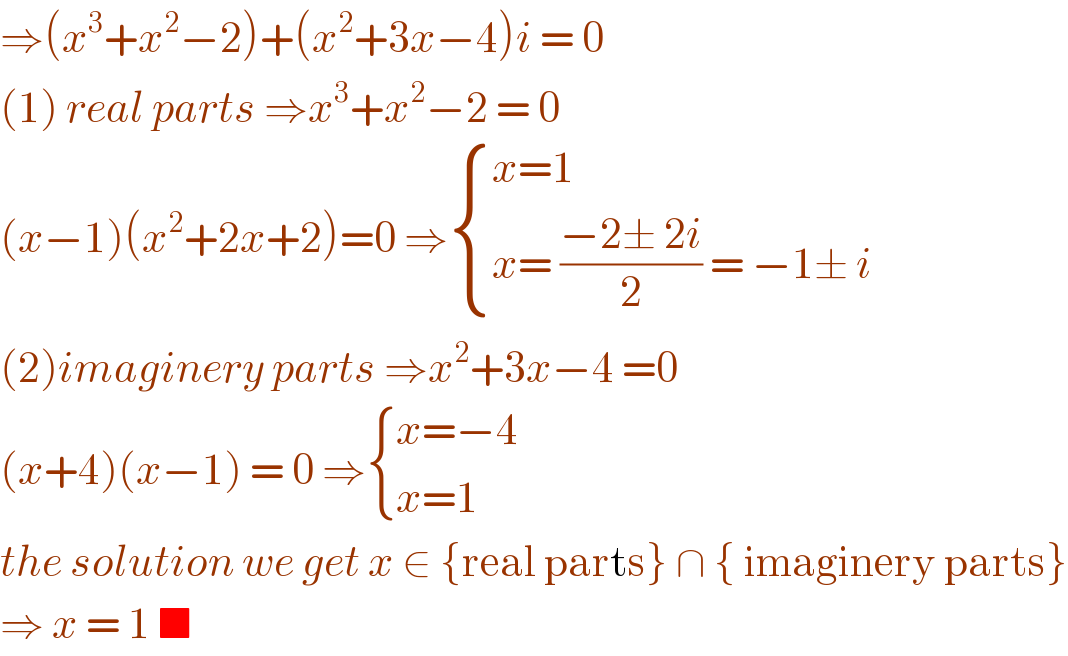
⇒(x^3 +x^2 −2)+(x^2 +3x−4)i = 0 (1) real parts ⇒x^3 +x^2 −2 = 0 (x−1)(x^2 +2x+2)=0 ⇒ { ((x=1)),((x= ((−2± 2i)/2) = −1± i)) :} (2)imaginery parts ⇒x^2 +3x−4 =0 (x+4)(x−1) = 0 ⇒ { ((x=−4)),((x=1)) :} the solution we get x ∈ {real parts} ∩ { imaginery parts} ⇒ x = 1 ■
$$\Rightarrow\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}\right)+\left({x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}\right){i}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{real}\:{parts}\:\Rightarrow{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}\:=\:\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)=\mathrm{0}\:\Rightarrow\begin{cases}{{x}=\mathrm{1}}\\{{x}=\:\frac{−\mathrm{2}\pm\:\mathrm{2}{i}}{\mathrm{2}}\:=\:−\mathrm{1}\pm\:{i}}\end{cases} \\ $$$$\left(\mathrm{2}\right){imaginery}\:{parts}\:\Rightarrow{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}\:=\mathrm{0} \\ $$$$\left({x}+\mathrm{4}\right)\left({x}−\mathrm{1}\right)\:=\:\mathrm{0}\:\Rightarrow\begin{cases}{{x}=−\mathrm{4}}\\{{x}=\mathrm{1}}\end{cases} \\ $$$${the}\:{solution}\:{we}\:{get}\:{x}\:\in\:\left\{\mathrm{real}\:\mathrm{parts}\right\}\:\cap\:\left\{\:\mathrm{imaginery}\:\mathrm{parts}\right\} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{1}\:\blacksquare \\ $$
Commented by MJS last updated on 15/Jun/20
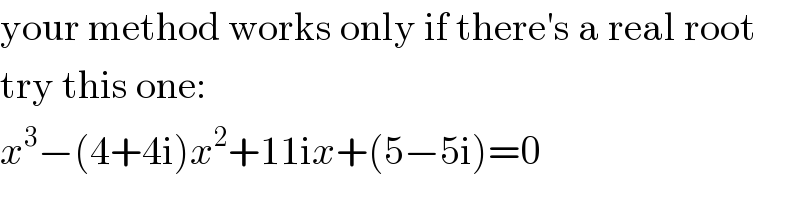
your method works only if there′s a real root try this one: x^3 −(4+4i)x^2 +11ix+(5−5i)=0
$$\mathrm{your}\:\mathrm{method}\:\mathrm{works}\:\mathrm{only}\:\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{real}\:\mathrm{root} \\ $$$$\mathrm{try}\:\mathrm{this}\:\mathrm{one}: \\ $$$${x}^{\mathrm{3}} −\left(\mathrm{4}+\mathrm{4i}\right){x}^{\mathrm{2}} +\mathrm{11i}{x}+\left(\mathrm{5}−\mathrm{5i}\right)=\mathrm{0} \\ $$
Answered by MJS last updated on 15/Jun/20
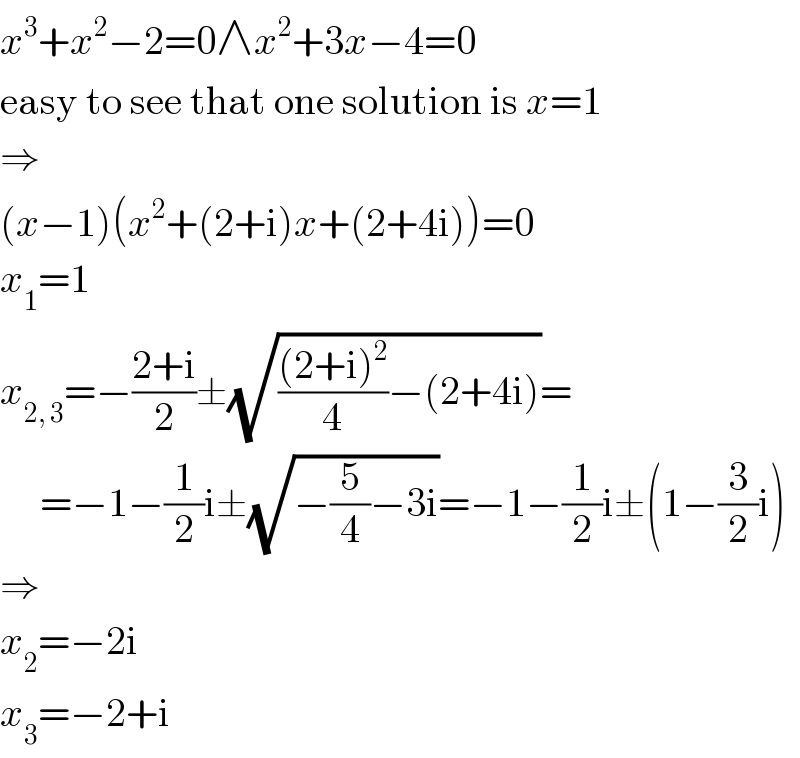
x^3 +x^2 −2=0∧x^2 +3x−4=0 easy to see that one solution is x=1 ⇒ (x−1)(x^2 +(2+i)x+(2+4i))=0 x_1 =1 x_(2, 3) =−((2+i)/2)±(√((((2+i)^2 )/4)−(2+4i)))= =−1−(1/2)i±(√(−(5/4)−3i))=−1−(1/2)i±(1−(3/2)i) ⇒ x_2 =−2i x_3 =−2+i
$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{0}\wedge{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{is}\:{x}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{i}\right){x}+\left(\mathrm{2}+\mathrm{4i}\right)\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{1} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{2}+\mathrm{i}}{\mathrm{2}}\pm\sqrt{\frac{\left(\mathrm{2}+\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{4}}−\left(\mathrm{2}+\mathrm{4i}\right)}= \\ $$$$\:\:\:\:\:=−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\pm\sqrt{−\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{3i}}=−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\pm\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{i}\right) \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{2}} =−\mathrm{2i} \\ $$$${x}_{\mathrm{3}} =−\mathrm{2}+\mathrm{i} \\ $$
Commented by bobhans last updated on 15/Jun/20
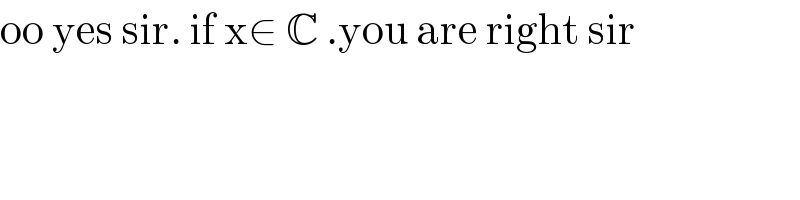
oo yes sir. if x∈ C .you are right sir
$$\mathrm{oo}\:\mathrm{yes}\:\mathrm{sir}.\:\mathrm{if}\:\mathrm{x}\in\:\mathbb{C}\:.\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir} \\ $$
Commented by bemath last updated on 15/Jun/20
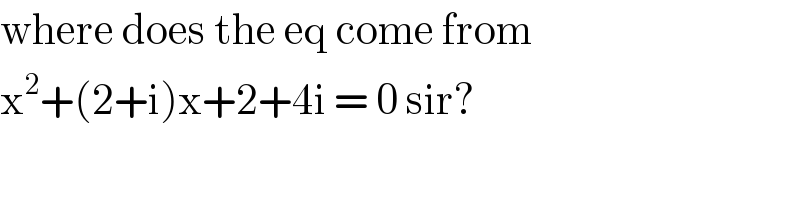
where does the eq come from x^2 +(2+i)x+2+4i = 0 sir?
$$\mathrm{where}\:\mathrm{does}\:\mathrm{the}\:\mathrm{eq}\:\mathrm{come}\:\mathrm{from} \\ $$$$\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}+\mathrm{2}+\mathrm{4i}\:=\:\mathrm{0}\:\mathrm{sir}? \\ $$
Commented by MJS last updated on 15/Jun/20
you can use long division
$$\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{long}\:\mathrm{division} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *